湍流燃烧的大涡模拟
近年来，湍流燃烧大涡模拟（LES, Large Eddy Simulation）迅猛发展，大涡模拟可将耗散尺度过滤，只求解大尺度脉动，其空间分辨率比雷诺时均方法RANS模型高，同时普适性也比RANS模型好。
大涡模拟可用于模拟复杂工程问题中的湍流流动和化学反应，可以解释湍流流动和化学反应的微观结构，可以对RANS模型的结果进行改善。尽管大涡模拟在计算上来说消耗的计算资源较为庞大，但它在湍流燃烧中的应用前景仍然十分广阔。
将湍流燃烧大涡模拟LES、雷诺时均方法RANS、直接数值模拟DNA三种方法进行对比：
RANS、LES、DNS优缺点比较
1. 网格可以较为粗糙
2. 结构较为简单
3. 计算消耗资源较少
1. 需建立相应的湍流模型
2. Kreith模型
3. RanzMarshall模型
1. 可以反映瞬态特征
2. 人工建立的湍流模型的影响得到减小（和RANS模型相比）
3. 液体蒸发携带的相变潜热
1. 需建立相应的湍流模型
2. 需要三维仿真
3. 网格需要很精细
4. 计算成本较高
在LES模型中待求解（大涡尺度）和不需求解的流动通过过滤函数分开：
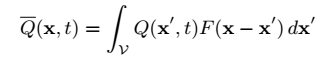
其中：
Q表示任意变量，如速度，质量分数，化学反应速率等；
υ表示整个计算域。
在整个计算域时，过滤函数满足归一化条件：
对于可变密度流动，引入质量加权滤波：
其中ρ表示密度。
在完成过滤后，对过滤后的变量可以给出连续性方程、动量方程和质量分数方程，
其中，
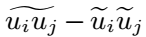为待求解的输运项；
滤波粘性
、分子通量
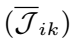和化学反应速率
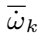需进一步给出求解方法。
1.2 亚格子模型
大涡模拟求解过程中需要对亚格子通量进行建模封闭，主要包括亚格子盈利和亚格子标量通量。
基于Boussinesq假设，可以得到：
其中υt为亚格子尺度粘度，同时满足：
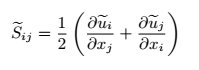
可以利用Smagorinsky模型以混合长度表示亚格子尺度粘度υt，
其中Δ是滤波尺寸，Cs是要调整的模型常数（通常为0.1≤Cs≤0.2）。
方程（7）中的各项同性贡献项可由Yoshizawa表达式表示，
其中Cl为模型常数。
大涡模拟可以利用已求解的流动运动来预测待求解区域的尺度效应。尺度相似性模型假设待求解的亚格子应力主要由最大的亚格子结构控制： 
其中已求解区域是精确过滤后的。
在LES仿真过程中，在不同网格尺寸需要对模型参数进行动态调整，例如方程（9）中的Cs，因此我们引入尺寸大于LES滤波器的尺寸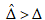
的测试滤波器
。
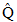在测试滤波器尺度上待求解的通量可以定义为：
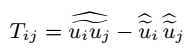
将方程（12）与的定义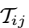
相结合，可以得到Germano恒等式：
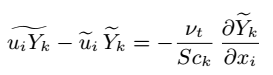
其中Sck是亚格子尺度的施密特数。
质量分数和能量方程中的过滤后反应速率需要相应的模型对其进行封闭。但是由于火焰锋面通常比网格尺寸更小，因此燃烧过程主要是亚格子尺度现象。过滤后反应速率的模型通常采用和RANS模型相同的方法。
2.1 预混燃烧模型
水平集方法将湍流预混火焰刷描述为一个传播的表面，可以通过该表面到火焰锋面的距离
进行描述：
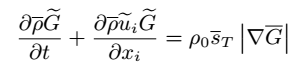
亚格子尺度的湍流火焰速度模型为：
其中，
为亚格子尺度湍流水平，α和n为模型参数。
火焰面密度模型将化学反应速率表示为：
2.2 非预混燃烧模型
非预混湍流火焰的大涡模拟通常基于概率密度函数，如此处所示，物种质量分数仅取决于一个变量z，例如混合物分数。过滤后质量分数由下式给出：
引入狄拉克δ函数，可以将方程（18）改写为：
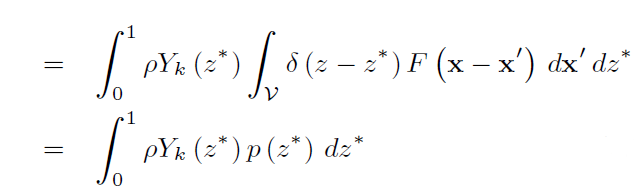
其中p（z *）是子网格尺度概率密度函数，可通过求解与RANS中的pdf平衡方程类似的平衡方程来推测得到。
混合分数的假定概率密度函数通常使用β函数：
其中参数a和b可以由下式给出：
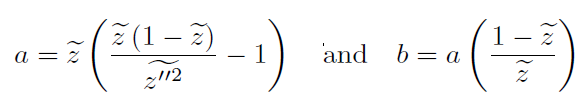
在大涡模拟中，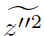
可以通过已求解量精确直接估计，
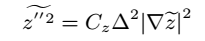
或相似性假设得到：
其中CZ为模型常数。
如图2所示为旋流燃气涡轮燃烧室，其通过切向喷射产生旋转流动，并通过中心毂稳定火焰和火焰，空气通过增压室供给。
在实验中，甲烷通过位于旋流器中的孔注入，在本计算假定甲烷和空气能够完全预混合。
图3给出了燃烧器中心平面上的实验和LES数值仿真得到的燃烧器中心平面上的轴向速度的时间平均值和RMS平均值分布。
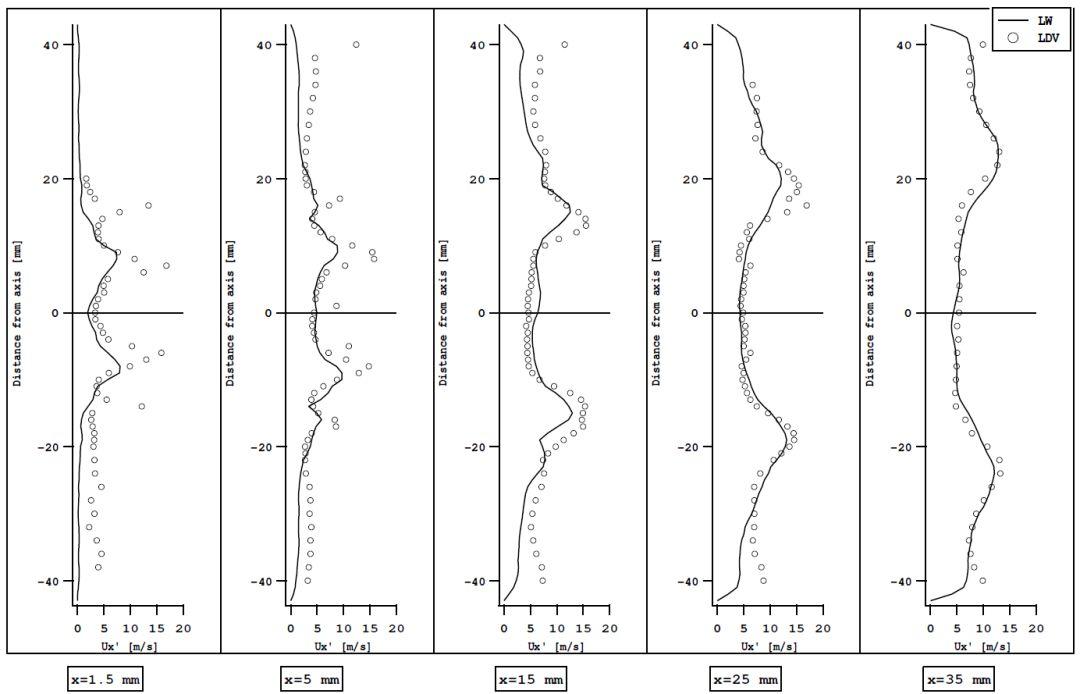
（b）RMS
可以看出，和实验结果对比，通过LES方法成功地再现了燃烧不稳定性，LES仿真结果和实验结果吻合度较高。
大涡模拟和RANS模型相比，具有较高的精度，和RANS在仿真模拟复杂结构湍流燃烧中具有巨大的潜力。虽然目前LES模型需要的计算资源较大，但随着硬件不断更新迭代，LES模型在未来燃烧科学研究中必将拥有广阔的应用前景。
【参考文献】
D. Veynante∗ . Large eddy simulations for turbulent combustion.
