预混湍流燃烧大涡模拟的一致水平集方法
预混燃烧一般发生在封闭体系中或混合气体向周围扩散的速度远小于燃烧速度的敞开体系中,燃烧放热造成产物体积迅速膨胀,压力升高,压强可达709.1-810.4KPa。
预混燃烧在燃烧前,燃料与氧气已经在燃烧器内充分混合。它是相对于扩散燃烧的另一种典型燃烧方式。
预混燃烧
预混湍流燃烧通常发生在较薄的火焰锋面,火焰的输运和反应放热,主要由火焰锋面输运过程和化学反应共同决定的。与模拟的几何尺度和大尺度湍流相比,火焰面的稀薄性带来了一个最主要的挑战。对于火焰面而言,其瞬时温度场基本上是不连续的,同时火焰面在不同时刻处于不同位置。针对LES模型而言,如果火焰面尺度小于滤波器尺寸,则温度场从未燃区域到已燃区域的变化在空间尺度上同样小于滤波器尺寸。
针对此问题可采用G方程进行求解,Williams等提出的G方程模型基于小火焰假设并采用水平集方法描述火焰锋面作为未燃烧气体和燃烧气体之间界面的演变。水平集函数G是所定义的标量场,使得火焰锋面位置处在G = G0,则未燃混合物对应G <G0。G方程式描述了与火焰锋面相关的界面的演变,作为水平集函数,即使对于极其薄的火焰面,它在火焰锋面两端也是连续的。
瞬时火焰表面的隐式表示为:
方程(1):
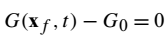
此处定义了水平集函数G。其中,t是时间,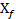 表示火焰锋面的位置。对方程(1)求微分可以得到:
表示火焰锋面的位置。对方程(1)求微分可以得到:
方程(2):
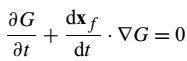
如果瞬时火焰锋面的曲率半径大于火焰面厚度,则火焰处于波纹小火焰状态,火焰锋面速度由下式给出:
方程(3):
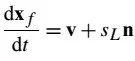
其中,v是局部流速, 是层流火焰速度。
是层流火焰速度。
注意,由于火焰几何形状,这可能与未拉伸的层流燃烧速度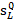 不同。例如,火焰向前输运导致在火焰表面形成尖点,这些尖点形成奇点中火焰输运速度高于。
不同。例如,火焰向前输运导致在火焰表面形成尖点,这些尖点形成奇点中火焰输运速度高于。
火焰法向矢量n被定义为指向未燃烧的区域,可以表示为:
方程(4):

将方程(2)和(3)组合得到瞬时G方程:
方程(5):
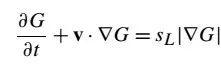
由于该方程来自方程(1)和(3),都只描述火焰表面,因此方程(5)仅在火焰表面有效。
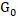 的位置可以定义为火焰中的任何位置,通常被定义为在未燃烧区域或燃烧侧。相对于未燃烧和燃烧的气体定义的燃烧速度分别表示为
的位置可以定义为火焰中的任何位置,通常被定义为在未燃烧区域或燃烧侧。相对于未燃烧和燃烧的气体定义的燃烧速度分别表示为 和
和 。
。
这里提出一个合适的LES滤波器,它将用于导出滤波后火焰锋面位置的水平集方程。火焰表面F的参数表示为:
方程(6):

其中,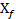 是火焰锋面位置,λ和μ是沿着火焰表面的曲线坐标形成与火焰锋面一起移动的正交坐标系。坐标λ和μ是函数的参数,在下文中记为:
是火焰锋面位置,λ和μ是沿着火焰表面的曲线坐标形成与火焰锋面一起移动的正交坐标系。坐标λ和μ是函数的参数,在下文中记为:

对于给定的参数组 ,空间滤波器
,空间滤波器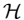 可以定义为
可以定义为
方程(7):

其中,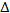 是过滤器宽度
是过滤器宽度
方程(8)

1 / S( ,t)是由归一化条件确定的因子
,t)是由归一化条件确定的因子
方程(9)
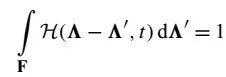
物理上,Mdλdu表示微元面积,S是滤波器内火焰的面积。滤波函数中使用的坐标不是空间坐标,而是火焰表面坐标。可以将用于火焰锋面位置的空间滤波操作定义为
方程(10)

该滤波操作如图1所示,表面坐标沿着瞬时火焰表面定义。

图1 瞬时和过滤的火焰锋面位置
图中,矩形表示过滤器,它连接到由小圆点指示的位置处的瞬时锋面。大圆点表示相应的滤波火焰锋面位置。虚线矩形表示不同λ位置的滤波器。
为了获得滤波的锋面位置,对于瞬时火焰表面上的每个点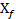 (
( ),方程式10滤波操作产生相应的平均火焰锋面位置
),方程式10滤波操作产生相应的平均火焰锋面位置 (
( )。这些位置
)。这些位置 (
( )定义了滤波后的火焰锋面位置。
)定义了滤波后的火焰锋面位置。
为了推导过滤火焰锋面位置的水平集方程,首先将过滤操作应用于方程式(3),得到:
方程(11):

由该方程给出的条件滤波的流速和输运项有:
方程(12):
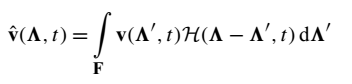
方程(13):
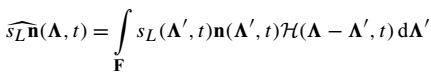
出现在方程式(13)中的层流燃烧速度不能当作常数。
由于滤波器随时间变化,滤波操作与时间导数无关。因此,使用此滤波器,我们无法确定滤波位置的位移速度,而只能确定瞬时锋面的滤波位移速度。为了获得滤波的火焰锋面位置的方程式,而不是过滤G场,引入新的水平集函数G,其描述滤波的火焰锋面位置的演变。过滤火焰表面的隐式表示如下:
方程(14):
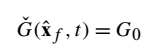
求微分得到:
方程(15):

我们使用由方程式(11)给出的未滤波前的滤波位移速度作为近似值,得到
方程(16):

如果使用交换滤波器,则对方程(15)的这种近似是精确的。将方程(11)代入方程(16)得到平均火焰锋面位置的G方程为:
方程(17):

方程式(13)中定义的输运项模型必须与过滤火焰锋面位置的法向量成比例。
方程(18):
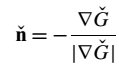
输运项有两个贡献,平均锋面随过滤层流燃烧速度和湍流子过滤器燃烧速度 的输运。因此:
的输运。因此:
方程(19):

滤后层流燃烧速度,作为沿子过滤器火焰锋面的条件平均值,可表示为:
方程(20):

其中,α代表影响层流燃烧速度的参数矢量,p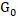 (α)是以火焰锋面位置为条件的所有α的联合概率密度函数。
(α)是以火焰锋面位置为条件的所有α的联合概率密度函数。
注意,根据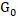 的定义,条件速度是火焰的未燃区域或燃烧侧的过滤速度。这些将分别由
的定义,条件速度是火焰的未燃区域或燃烧侧的过滤速度。这些将分别由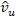 和
和 表示。类似地,湍流燃烧速度必须相对于未燃区域或燃烧侧的气体来定义,用
表示。类似地,湍流燃烧速度必须相对于未燃区域或燃烧侧的气体来定义,用 和
和 表示。使用这些符号,取决于
表示。使用这些符号,取决于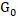 的定义,方程式(17)可以写成:
的定义,方程式(17)可以写成:
方程(21):
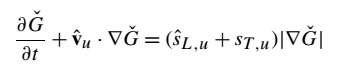
方程(22):
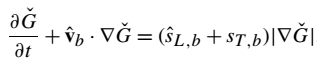
过滤的火焰锋面位置的演变可以用方程(21)或方程(22)来描述。
条件速度是火焰锋面处的速度,用滤波器函数H加权并在滤波器体积内的整个火焰表面上平均得到。可以将局部速度近似为:
方程(23)
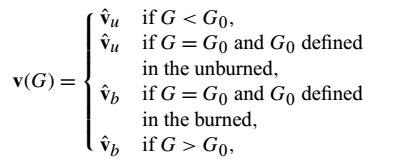
可以得到条件的Favre滤波速度
方程(24)
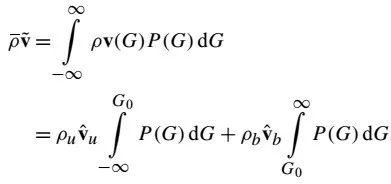
其中P(G)是G的概率密度函数。可以得到燃烧混合物 的概率:
的概率:
方程(25):
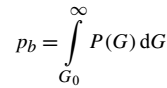
无条件速度可以写成
方程(26):

类似地,无条件滤波的密度可以导出为
方程(27):

为了用表达,我们将使用跳跃条件来得到平均火焰面两侧的流量平衡,由下式给出
方程(28):

位移速度可由方程式(11)表示,其中条件速度和燃烧速度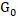 的选择取决于相对于火焰的位置。如果定义在未燃烧区域,则必须使用
的选择取决于相对于火焰的位置。如果定义在未燃烧区域,则必须使用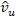 和
和 。而如果在燃烧侧,那么
。而如果在燃烧侧,那么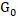 将由
将由 和
和 给出。对于穿过火焰锋面的速度跳跃,有:
给出。对于穿过火焰锋面的速度跳跃,有:
方程(29):

如果定义在未燃烧侧,则
方程(30):

将方程式 (29)代入方程(26)得到以无条件速度表示的条件速度的表达式:
方程(31):
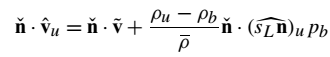
将对流项分为火焰法向和火焰切向部分。由于火焰切向部分仅影响火焰锋面的平行平移并且对火焰传播没有影响,因此可以忽略它。方程(21)的对流项可以写成
方程(32):
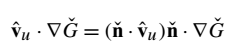
将方程(31)代入方程(32)给出的正常对流项后,得到:
方程(33):
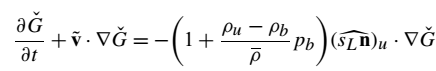
使用方程(27),滤波后的火焰锋面位置的方程式可以写成
方程(34):

使用来自方程式(19)的滤波输运项的表达式得到
方程(35):

类似地,从将方程式(30)代入方程(26),在燃烧气体中定义的方程可以导出为
方程(36):

因为流量守恒,火焰必须满足下式:
方程(37):
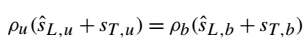
通过方程(37),也可以容易地看出方程(35)和(36)是等价的。
在推导薄反应区瞬时G方程的过程中,Peters从瞬时温度方程出发,导出了由T(x,t)=T0给出的温度等值面的能级集方程,其中是T0内层温度。输运速度的表达式类似于方程(3),在这里位移速度Sd可以写成
方程(38):
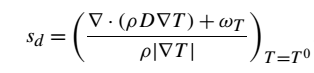
其中, 是密度,D是温度扩散系数,ωT是化学反应源项。当温度等值面法向量
是密度,D是温度扩散系数,ωT是化学反应源项。当温度等值面法向量 时,方程(38)中的输运项可以用面法线和切线的分量T0表示:
时,方程(38)中的输运项可以用面法线和切线的分量T0表示:
方程(39):

方程(40):
Sd 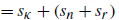
在薄的反应区域中,由于温度等值面T=T0将由G=G0描述,因此Sk可写为
方程(41):

使用方程式(10)给出的过滤操作过滤(41)会得到:
方程(42):
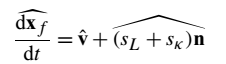
将方程(42)代入方程(16)从而得到对波纹小火焰和薄反应区有效的G方程
方程(43):
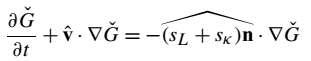
本文为湍流预混燃烧的大涡模拟(LES)提供了一致的水平集公式,使用新的滤波技术导出平均火焰锋面位置的控制水平集方程,并提供火焰锋面条件速度和输运项的模型。
【参考文献】
H. Pitsch. A consistent level set formulation for large-eddy simulation of premixed turbulent combustion. Combustion and Flame 143 (2005) 587–598.




