浓相气固流动模型:MP-PIC
浓相气固流动模拟方法
目前,浓相气固流动模拟方法根据对颗粒离散相的描述方式主要分为两类:
欧拉-欧拉(Eulerian-Eulerian)方法;
欧拉-拉格朗日(Eulerian-Lagrangian)方法。
欧拉-欧拉方法主要以采用颗粒动力学模型(KineticTheory of Granular Flows-KTGF)作为固相封闭模型的双流体模型(TFM)为代表,其将气相和固相作为相互渗透的连续相,因而在计算规模和计算精度上都得到一定程度的保证。
欧拉-拉格朗日方法将颗粒作为离散相描述,由于描述尺度的不同以及颗粒作用间的模型不同,欧拉-拉格朗日细分出众多方法。其中最具代表性的是计算流体力学耦合离散元模型的方法CFD-DEM,将气相用连续相描述,而对每个固相颗粒进行追踪并详细计算颗粒间的碰撞过程。双流体模型可以模拟较大规模的装置,但不能对颗粒尺度的流动进行解析。离散元模型能准确模拟颗粒间作用力,适用于返料系统中各种复杂流型,但计算非常耗资源,能模拟的颗粒数较少,无法做大尺度的气固流动模拟,限制了其在工业领域的应用。近年来,兼顾了双流体模型和离散元模型优点的MP-PIC方法得到越来越多的应用。
1
MP-PIC
多相质点网格模型MP-PIC(Multiphase Particle-in-cell)作为混合型欧拉-拉格朗日方法,气相的流动采用体积平均N-S控制方程组描述,颗粒相用数值粒子进行离散,对每个粒子都进行追踪从而获得颗粒相在不同时刻的空间分布,在需要知道颗粒相整体特性时则将所有颗粒属性都插值到流体网格进行求解,从而使颗粒相同时具有离散相和连续相的性质。
MP-PIC特点
1 | 不同于CFD-DEM,MP-PIC使用数值粒子(Parcel)概念表示颗粒相,并使用连续的颗粒应力模型阻止颗粒被过度堆积而超出允许的物理极限; |
2 | MP-PIC方法将颗粒相群体的特性映射到欧拉网格来计算连续颗粒应力场,而每个数值颗粒都具有独立的速度和位置,并通过积分牛顿运动方程不断更新其速度和位置,从而使其同时具有了TFM和CFD-DEM两者的特点; |
3 | MP-PIC能计算大规模颗粒系统气固流动,同时还能对固相在颗粒尺度进行描述。 |
图1对不同的浓相气固流动模型进行了对比,可以看到:DEM模型具有更高的解析度,但耗时最多;TFM计算耗时次之;MP-PIC虽能计算大规模颗粒系统气固流动,同时能对固相在颗粒尺度进行描述,但由于使用的子模型最多,因而计算结果的准确性最差。在选择模型,一定要根据自身应用的需求正确选择。

图1 浓相气固多相流模型
2
气相控制方程
气相流动用基于体积平均的连续性和动量方程描述为:
方程(1)

方程(2)
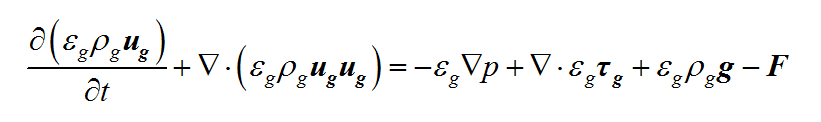
方程(2)中气相应力 可以用方程(3)计算,其中气相有效动力粘度
可以用方程(3)计算,其中气相有效动力粘度 包括了层流粘度和湍流粘度:
包括了层流粘度和湍流粘度:
方程(3)
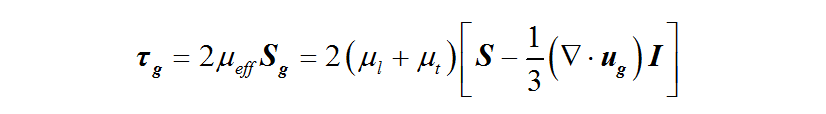
气相压力和密度间的关系可通过理想气体状态方程表示:
方程(4)
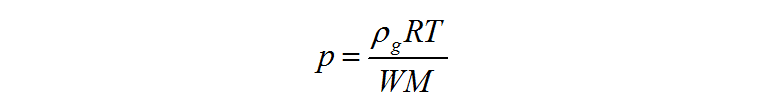
流场中任意点的气相和固相的体积分数满足:
方程(5)

3
固相控制方程
颗粒相在空间中分布用概率分布函数(PDF)描述f (x,ug,ρp ,Vp,t ),其表示t时刻在位置x到具有速度为ug,密度为ρp 和体积为Vp的颗粒的概率,f 随时间t 的演变规律[1]表示为:
方程(5)
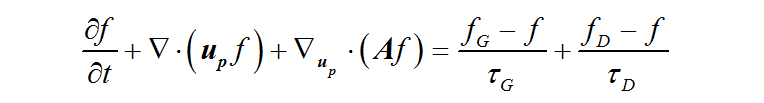
在实际的数值求解过程中,颗粒相的空间分布通过将概率分布分解为有限数量的数值粒子,并追踪这些粒子的运动过程来获得,而每个数值粒子表示一定数量的具有相同密度、体积、速度和位置的真实颗粒。由于使用数值粒子,从而极大地减少了计算需求,同时在大多数条件下不会降低计算结果的准确度。此外,通过对单个粒子赋予属性从而可以使MP-PIC方法很自然地模拟具有粒径分布的颗粒及多类型多粒径的颗粒。

图2 数值颗粒示意图
通过颗粒的概率分布函数f,可以很方便地对其积分而得到颗粒的体积分数分布:
方程(7):

颗粒相的其它整体属性如平均颗粒速度 和平均密度
和平均密度 也可以通过相同的方式求得。
也可以通过相同的方式求得。
在每个时间步,每个计算粒子的位置和速度更新基于牛顿运动方程计算得到:
方程(8):

方程(9):
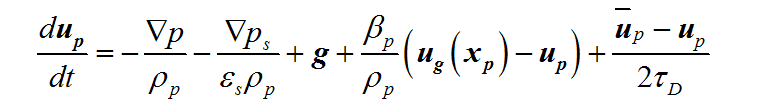
类似于双流体模型,MP-PIC中的碰撞力也可以分为粘性应力和摩擦应力。粘性应力表示稀相时的二元碰撞而摩擦应力表示高浓度下的长时间接触力。MP-PIC中只使用摩擦应力主对角元素的梯度,其作用是为了防止颗粒过度堆积而超出颗粒体积浓度所允许的物理极限值。
为了正确表征颗粒碰撞过程,可以在颗粒输运方程中加入一个BGK项来表示碰撞作用对颗粒波动速度的阻尼作用。MP-PIC通过在颗粒分布函数的演变方程中加入了阻尼模型和各向同性模型来表示颗粒的稀相碰撞作用,这两项通过对颗粒速度进行修正从而更加准确地描述颗粒间相互作用过程。颗粒连续方程右边两项分别表示碰撞趋于各向同性力[2](Return-to-isotropy force)和碰撞阻尼力[3](Damping force)对颗粒分布的影响。前者表示各向异性速度分布趋向与高斯各向同性分布的弛豫过程,后者则表示相对运动颗粒间的阻尼过程,即颗粒速度趋向于质量平均速度的弛豫过程。
方程(10):

由于在浓相气固流中,颗粒碰撞极为频繁,因此采用一个考虑颗粒恢复系数和速度非平衡分布对阻尼时间作用的改进模型。最终的模型是一个平衡模型,且关键在于阻尼时间的求解。
时间尺度模型
方程(11):
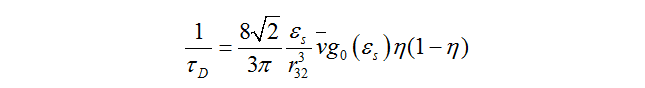
其中:

为平均碰撞频率。
因而碰撞对颗粒速度的作用,
方程(12):

其中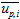 网格平均颗粒速度在颗粒点位置的插值。
网格平均颗粒速度在颗粒点位置的插值。
各向同性模型假设颗粒分布函数收敛到最终分布的时间正比于两个弛豫时间的倒数。
方程(13)

方程(14)

不同于阻尼模型将弛豫时间直接用于速度修正,各向同性模型对速度修正分两步进行。
对颗粒云中的每个粒子生成一个随机数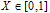
如果

方程(15):

否则,
方程(16):

或

由于只对有限数量粒子取样从而会导致网格内平均速度和速度变量(颗粒温度)不守恒。需要进行守恒修正:
方程(17):
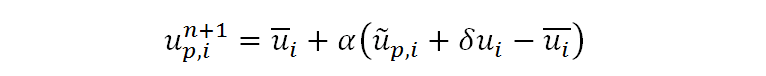
或
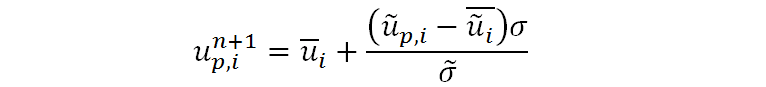
除了颗粒间的法向作用力,在一些非流化的区域,颗粒相互挤压并存在相对运动。此时,颗粒间还存在着切向摩擦力,基于网格的平均静和动摩擦可以用以下方程表示,
方程(18):
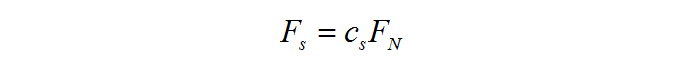
式中cs为摩擦系数,通常由实验来确定。
【参考文献】
[1] Snider, D.M., An Incompressible Three-Dimensional Multiphase Particle-in-Cell Model for Dense Particle Flows. Journal of Computational Physics, 2001. 170(2): p. 523-549.
[2] O'Rourke, P.J. and D.M. Snider, Inclusion of collisional return-to-isotropy in the MP-PIC method. Chemical Engineering Science, 2012. 80: p. 39-54.
[3] O’Rourke, P.J. and D.M. Snider, An improved collision damping time for MP-PIC calculations of dense particle flows with applications to polydisperse sedimenting beds and colliding particle jets. Chemical Engineering Science, 2010. 65(22): p. 6014-6028.




