Kelvin–Helmholtz不稳定性
1
剪切流的不稳定性
剪切流的不稳定性长久以来被人们关注。当速度场中存在梯度时(比如边界层内的速度场),流场中可能会存在不稳定性,这些不稳定性有利于扰动的发展。
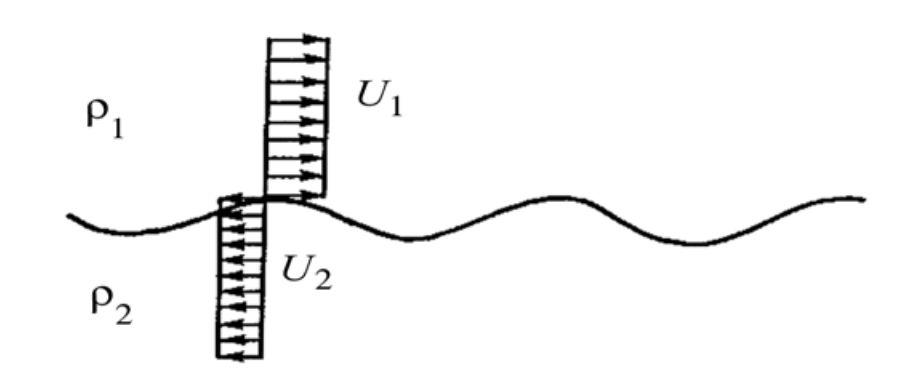
剪切流示意图
拓跋野提到的开尔文-亥姆霍兹不稳定性指的就是平行剪切流间的不稳定性。这种不稳定性在自然界中可以诱发许多现象。
 |
 |
 |
微风带起的水面波纹可以简化为两层流速不同的平行流体在交界面处出现的扰动。
关于二维平行流界面处开尔文-亥姆霍兹不稳定性存在的条件,这里就不详细推导了。基本思想就是基于无粘的假设,从非定常Bernoulli方程出发,以势函数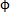 的形式引入波形扰动 (wave-like perturbation), 将扰动代入非定常Bernoulli方程,最后求解相速度c,确保其没有虚部,得到不稳定性存在的必要条件为:
的形式引入波形扰动 (wave-like perturbation), 将扰动代入非定常Bernoulli方程,最后求解相速度c,确保其没有虚部,得到不稳定性存在的必要条件为:
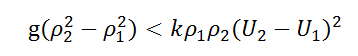
其中k为平面波的波数。
2
Kelvin-Helmholtz 实验
实验做法比较简单,但是操作起来得小心。在可密封的水槽内注入两种染色的不同液体:水和盐水。先在水槽内注入约一半的水,染色的盐水通过底部进水口缓慢注入。最后加满水槽后确保槽内无气泡,将其小心地置于水平位置。开始实验时将水槽倾斜,盐水朝下流动,与向上运动的水在交界面处产生剪切流,很快便能形成明显的涡结构。
视频来自腐国诺丁汉大学工程学院某实验室
采用OpenFOAM自带的interFoam模拟两层流体交界面处的KH不稳定性现象。熟悉OpenFOAM的读者可能知道,interFoam是基于Volume of fluid (VOF方法) 求解两相不可压流体的基础求解器。此方法中则定义了一个变量α来表示流体的相分数。
考虑某一个网格单元的气液两相系统,如果此网格单元内充满了流体,则α=1;如果此网格单元内充满了气体,则α=0。如果α的值介于0和1之间,则此网格单元内为气液混合。VOF的两相流界面需要对每个网格内的相场值进行后处理才可以得到。
CFD网格在Pointwise中建立,给所有domains分配边界条件后导出为OpenFOAM的网格,置于polyMesh文件夹内。需要注意的是,第三方网格绘制软件导出OpenFOAM网格时,除要运行checkMesh外,最好运行下renumberMesh这个utiltity。
code: renumberMesh -overwrite
renumberMesh的主要作用是对各个cellElement的ID重新排序,使离散偏微分方程组产生的系数矩阵带宽(bandwidth) 变小,使之更接近对角矩阵,这样可以减轻求解代数系统的压力。例如,下图中展示了运行renumberMesh后,某个网格文件中各个单元的ID分布的变化情况(详细请参阅http://caefn.com/openfoam/utilities-renumbermesh)。
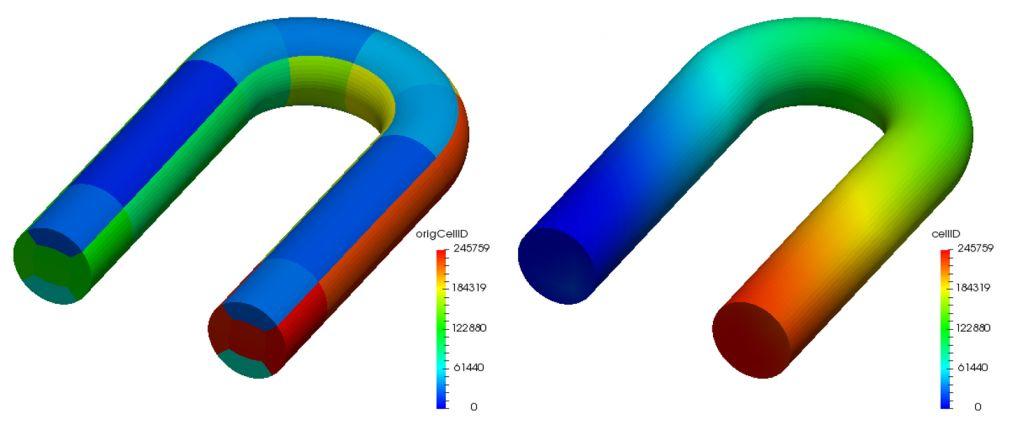
运行renumberMesh后某网格文件中各单元ID分布变化
笔者曾经试过不运行renumberMesh直接用pointwised生成的OpenFOAM网格 (网格量十几万) 进行计算,然鹅,矩阵求解器第一步就崩掉了😳,报出float point exception 的错误,运行renumberMesh后运算就没有问题了。
计算区域为0.05m×0.05m×1.00m竖直方管,顶部与底部均封闭。
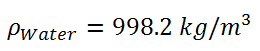
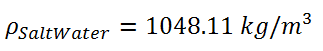
由于重力场的作用,两种密度不同的液体会产生相对运动,盐水会沉到底层,水会向上浮。未充分混合前,在交界面处两相的z方向速度相反。两种液体交界面处满足KH不稳定性条件,会出现不稳定的涡的结构。由于在界面处后面会出现涡结构,建议加密这里的网格。为了节约计算资源,这里的网格实际为二维网格,即前后两个面(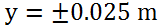 )的patch类型为empty。
)的patch类型为empty。
物性参数在constant/ transportProperties里,重力加速度在constant/ g文件里被定义。
这里interFoam采用层流模型,考虑二维平行流的剪切,湍流模型在这里可以关掉。初始场的盐水域可利用setFields 设置,即alpha.salt=1; 其余区域为水, alpha.salt=0.

模型设置
Tips:
setFieldsDict文件的查找与拷贝,在OpenFOAM 6.0中可以运行foamGet这个utility,选择要拷贝的源文件,运行后选中的字典文件就被自动拷贝至system文件目录下。
Code: foamGet setFieldsDict
setFieldsDict具体设置如下:

注意:boxToCell中box的两个顶点坐标最好不要选择网格和边界的顶点坐标,而是应该选择比那些顶点坐标值略大些的数值,确保设定的区域完全被box包住, 因为实际网格顶点坐标可能与预设的坐标值要差个1e-5或者1e-6,与网格软件设定tolerance有关。
当然也可以利用pyFoam中的pyFoamCreateBoundaryPatches.py和pyFoamWriteDictionary.py定义设置初始场和controlDict。
边界条件的设置: 对于速度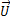 来说,四周壁面及顶部底部均选用noslip无滑移边界条件;压强p_rgh在所有壁面均选用fixedFluxPressure, gradient和value均为零。此处的p_rgh用以更新下一时间步的压强:
来说,四周壁面及顶部底部均选用noslip无滑移边界条件;压强p_rgh在所有壁面均选用fixedFluxPressure, gradient和value均为零。此处的p_rgh用以更新下一时间步的压强:

Alpha.water和alpha.salt在所有壁面上均选用zeroGradient边界条件。
计算时采用可变时间步长,限制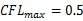 .
.
运行的alpha.salt相含率随时间的变化在paraview可以看到两种液体的界面处的涡结构。(视频截取时间段为3-4s)
两种液体的界面处的涡结构

两种液体的界面处的涡结构(局部放大)
不难发现,此网格用FV计算很难展现涡的细致结构。
OpenFOAM中还有一个基于interFoam的自适应网格加密(adaptive meshrefinement) 多相流求解器: interDyMFoam,它会在两相交界处根据某个场的数值范围来加密网格,从而达到细致锐化两相交界面的作用。然鹅,加密后的网格细致了,却会造成当地的CFL数骤增,当依据最大CFL的限制开启可变时间步长时,时间步长可能会缩小好几个量级,这就大大延长了模拟的时间。
当然,还可以采用更高阶的离散格式,比如近来流行的间断伽辽金方法(Discontinuous Galerkin Method) ,基本思想是将NS方程投影 (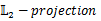 ) 至正交基函数张成的空间中,得到的投影值对所有控制体积积分令其为零,再求解一个由类质量矩阵,类刚度矩阵构成的代数系统。此方法可以看成是有限元法 (FEM) 和有限体积法 (FVM) 生出来的混血儿。
) 至正交基函数张成的空间中,得到的投影值对所有控制体积积分令其为零,再求解一个由类质量矩阵,类刚度矩阵构成的代数系统。此方法可以看成是有限元法 (FEM) 和有限体积法 (FVM) 生出来的混血儿。
下面视频里的模拟就用到了四阶格式的DG法与自适应网格加密,展现了KH不稳定性诱发的涡结构细节。
视频来自德国海德堡大学理论研究院




