激波与颗粒群相互作用的研究小谈
颗粒流
自然界中存在很多颗粒流现象,如沙丘演化、泥石流、滑坡、雪崩等,在工农业生产及能源环保等领域也有广泛应用。高速气体和固体颗粒群相互作用是颗粒流的一个重要分支,它广泛存在于天文、自然灾害、工业安全、医疗工业和国防等领域,例如超新星爆炸[3]、火山爆发[4]、粉尘爆炸[5]、无针注射[6]等。

图1 超新星爆炸示意图

图2 火山喷发

图3 粉尘爆炸
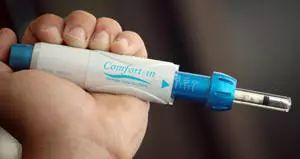
图4 无针注射
在高速颗粒流中颗粒体积分数是一个重要参数[7]。
当 时,颗粒之间彼此远离,颗粒间碰撞效应忽略不计[8];
时,颗粒之间彼此远离,颗粒间碰撞效应忽略不计[8];
当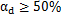 ,颗粒之间彼此靠近,颗粒间碰撞是它们运动的主要机制,流体对固体颗粒的作用可以忽略不计[9];
,颗粒之间彼此靠近,颗粒间碰撞是它们运动的主要机制,流体对固体颗粒的作用可以忽略不计[9];
当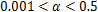 时,需同时考虑颗粒与颗粒之间以及颗粒与流体之间的相互作用[10],这使得问题的求解变得复杂。
时,需同时考虑颗粒与颗粒之间以及颗粒与流体之间的相互作用[10],这使得问题的求解变得复杂。
对于激波与颗粒群相互作用已经有一些学者开始从实验上[11–13]和数值上[14–16]进行了研究。本文主要介绍Jiang等人[17]和Deng等人[18]提出的基于分层多相流[19]的数值方法对激波与二维圆柱云相互作用前期的研究,以及激波与三维圆球云相互作用后期的研究。
图1显示了马赫数为1.67的入射激波与二维圆柱云相互作用的压强分布图,在无量纲时间t=2.4和3.5时,流场中的反射激波和透射激波清晰可见。分析流场中的内能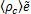 、动能
、动能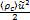 和湍动能
和湍动能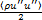 。
。
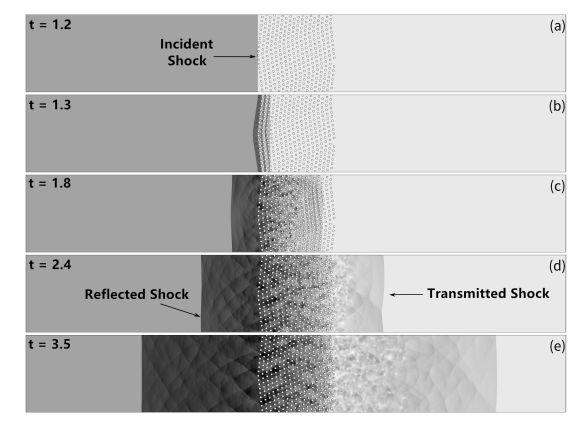
如图2所示,可以发现流场内能比动能和湍流能大一个数量级,流场湍动能主要分布在圆柱云区域以及圆柱云下游区域,同时在此区域流场的湍动能和流场动能在相同数量级。

通过使用简化的一维体积平均模型[10, 20],可以拟合直接数值模拟(DNS)结果,如图3所示。
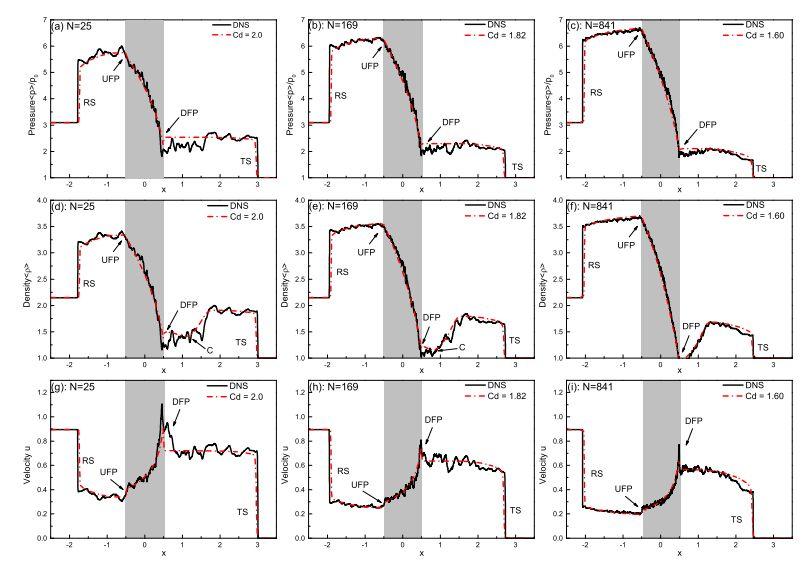
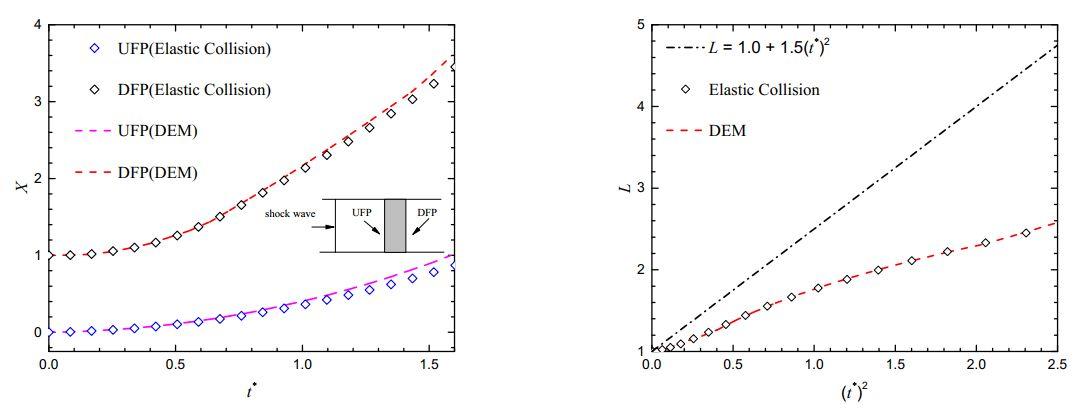
图3中浅灰色 区域代表圆柱云区域,这里显示了流场中25,169和841个圆柱的情况,图中RS表示反射激波,UFP代表圆柱云上边缘,DFP代表圆柱云下边缘,C表示接触间断,TS表示透射激波[17]。
参考文献
1. Campbell, C.S.: Rapid Granular Flows. Annual Review of Fluid Mechanics. 22, 57–90 (1990). doi:10.1146/annurev.fl.22.010190.000421
2. Jaeger, H.M., Nagel, S.R.: Physics of the granular state. Science. 255, 1523–1531 (1992)
3. 罗志全: 核心坍缩型超新星的相关物理过程及爆发机制的研究, (2006)
4. Chojnicki, K., Clarke, A.B., Phillips, J.C.: A shock‐tube investigation of the dynamics of gas‐particle mixtures: Implications for explosive volcanic eruptions. Geophysical Research Letters. 33, 292–306 (2006)
5. 张莉聪, 徐景德, 吴兵, 杨庚宇: 甲烷-煤尘爆炸波与障碍物相互作用的数值研究. 中国安全科学学报. 85-88+1 (2004)
6. Quinlan, N.J., Kendall, M. a. F., Bellhouse, B.J., Ainsworth, R.W.: Investigations of gas and particle dynamics in first generation needle-free drug delivery devices. Shock Waves. 10, 395–404 (2001). doi:10.1007/PL00004052
7. Zhang, F., Frost, D.L., Thibault, P.A., Murray, S.B.: Explosive dispersal of solid particles. Shock Waves. 10, 431–443 (2001). doi:10.1007/PL00004050
8. Rudinger, G.: Fundamentals of gas-particle flow. Elsevier Scientific Pub. Co. (1980)
9. Goetsch, R.J., Regele, J.D.: Discrete element method prediction of particle curtain properties. Chem. Eng. Sci. 137, 852–861 (2015). doi:10.1016/j.ces.2015.07.034
10. Regele, J.D., Rabinovitch, J., Colonius, T., Blanquart, G.: Unsteady effects in dense, high speed, particle laden flows. Int. J. Multiph. Flow. 61, 1–13 (2014). doi:10.1016/j.ijmultiphaseflow.2013.12.007
11. Wagner, J.L., Beresh, S.J., Kearney, S.P., Trott, W.M., Castaneda, J.N., Pruett, B.O., Baer, M.R.: A multiphase shock tube for shock wave interactions with dense particle fields. Exp. Fluids. 52, 1507–1517 (2012). doi:10.1007/s00348-012-1272-x
12. Wagner, J.L., Kearney, S.P., Beresh, S.J., DeMauro, E.P., Pruett, B.O.: Flash X-ray measurements on the shock-induced dispersal of a dense particle curtain. Exp. Fluids. 56, 213 (2015). doi:10.1007/s00348-015-2087-3
13. Theofanous, T.G., Mitkin, V., Chang, C.-H.: The dynamics of dense particle clouds subjected to shock waves. Part 1. Experiments and scaling laws. Journal of Fluid Mechanics. 792, 658–681 (2016). doi:10.1017/jfm.2016.97
14. Ling, Y., Wagner, J.L., Beresh, S.J., Kearney, S.P., Balachandar, S.: Interaction of a planar shock wave with a dense particle curtain: Modeling and experiments. Physics of Fluids. 24, 113301 (2012). doi:10.1063/1.4768815
15. Theofanous, T.G., Chang, C.-H.: The dynamics of dense particle clouds subjected to shock waves. Part 2. Modeling/numerical issues and the way forward. International Journal of Multiphase Flow. 89, 177–206 (2017). doi:10.1016/j.ijmultiphaseflow.2016.10.004
16. Theofanous, T.G., Mitkin, V., Chang, C.-H.: Shock dispersal of dilute particle clouds. Journal of Fluid Mechanics. 841, 732–745 (2018). doi:10.1017/jfm.2018.110
17. Jiang, L.-J., Deng, X.-L., Tao, L.: DNS Study of Initial-Stage Shock-Particle Curtain Interaction. Commun. Comput. Phys. 23, 1202–1222 (2018). doi:10.4208/cicp.OA-2016-0256
18. Deng, X., Jiang, L., Ding, Y.: Direct Numerical Simulation of Long-term Shock-particle Curtain Interaction. In: 2018 AIAA Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics (2018)
19. Chang, C.-H., Liou, M.-S.: A robust and accurate approach to computing compressible multiphase flow: Stratified flow model and AUSM(+)-up scheme. J. Comput. Phys. 227, 5360–5360 (2008). doi:10.1016/j.jcp.2008.01.041
20. Crowe, C., Schwarzkopf, J., Sommerfeld, M.: Multiphase Flows with Droplets and Particles. CRC PRESS-TAYLOR & FRANCIS GROUP, 6000 BROKEN SOUND PARKWAY NW, STE 300, BOCA RATON, FL 33487-2742 USA (2012)
21. Kuwabara, G., Kono, K.: Restitution coefficient in a collision between two spheres. Japanese journal of applied physics. 26, 1230 (1987)




