基于神经网络算法的OpenFOAM燃烧求解器
本文通过预先求解层流火焰面方程,建立以混合分数Z和反应进度变量Yc为查表变量层流火焰面表。以火焰面表为样本基于BP算法训练神经网络,实现对Z、Yc与显焓、组分质量分数之间非线性函数关系的逼近,以此为基础在OpenFOAM平台上开发基于神经网络算法的燃烧求解器annReactingFoam。对轴对称伴流甲烷/空气非预混层流火焰的模拟结果表明,使用annReactingFoam计算得到的温度及组分质量分数分布与求解详细化学反应得到的结果较为吻合。
1
研究背景

图1 典型的神经网络结构图
本文介绍了基于OpenFOAM平台[6]开发的神经网络燃烧求解模块。通过自主开发的程序调用CHEMKIN-III模块[7]完成层流火焰面建表,将火焰面表作为样本基于Keras框架[8]采用BP算法训练神经网络,实现对Z、Yc 与显焓、组分质量分数之间非线性函数关系的逼近,并开发了基于神经网络算法的OpenFOAM燃烧求解器annReactingFoam。
2
理论依据及程序实现
层流火焰面建表
火焰面模型适用的前提为燃烧的化学反应速率远快于湍流时间尺度,湍流火焰可视为一系列层流小火焰的集 合。通过求解一系列不同拉伸率下的层流对撞扩散火焰(图2),可得到表征层流小火焰结构的层流火焰面解。

混合分数Z 坐标下的层流火焰面方程为如下:
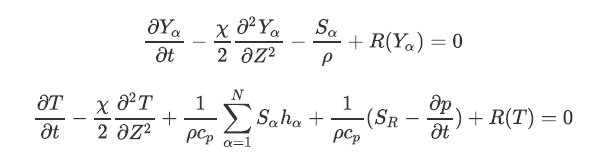
式中:Yα,Sα,hα 分别对应第α种组分的质量分数、反应速率和焓。在薄反应区和准一维的假设下,R(Yα),R(T)是高阶小量,可以忽略。选取混合分数Z 以及反应进度变量Yc 作为建表变量,建立包含显焓、组分质量分数、Yc 生成率ώYc的层流火焰面表,其中Yc 定义为CO2和H2O的质量分数之和[9]。此处与传统火焰面建表方法的不同在于选取显焓而非温度建表,其原因在于OpenFOAM中的热物理模型是基于显焓值计算温度及其他热物性的值。本文建立了甲烷/空气对撞火焰的层流火焰面表,选取的化学反应机理为GRI-3.0机理,得到的火焰面表中显焓和CO2质量分数分布在Z-Yc 坐标下的分布如图3所示。


图3 显焓、CO2质量分数在Z-Yc 坐标下的分布
神经网络的训练
利用Keras搭建网络主要有以下几步:
1 | 选择模型,Keras提供了序贯式模型和函数值模型两种; |
2 | 搭建网络层,包括输入层、输出层、隐藏层; |
3 | 编译,包括选择优化函数、损失函数; |
4 | 训练网络; |
5 | 利用验证集预测数据。 |

隐含层选择Tanh激活函数,输出层选择线性激活函数。设置完成后,不断迭代训练神经网络,等到MSE值不再减小时停止训练网络。

图4 基于火焰面数据表的神经网络结构图
为了验证得到的神经网络对火焰面表输入/输出变量间函数关系的还原精度,将训练集中的输入值重新代入训练好的神经网络,并将预测得到的输出值(ANN Prediction)与原有火焰面表中对应的目标值(Target)相比较。
图5展示了显焓及CH4、CO2和H2O组分质量分数预测值与目标值的对比,可以看出,神经网络能达到较高的还原精度。

annReactingFoam
本文基于OpenFOAM的标准燃烧求解器reactingFoam开发了基于神经网络算法求解的新型燃烧求解器annReactingFoam。该求解器在原有燃烧求解器的基础上,添加了变量Z 和上步的Yc 的输运方程以及自主开发的神经网络预测模块,其计算流程如图6所示。

图6 annReactingFoam工作流

式中Z 为场类的对象,包含场中所有节点的数据值,可采用forall函数遍历场中节点。
神经网络预测模块包括模型参数的读取、网络预测值的计算两部分。在Keras框架下,读取2.2中训练好的网络模型,将可以复现网络的权重、偏置分别写入求解器中的权重矩阵和偏置矩阵,并记录激活函数;网络预测值计算部分与BP算法中的正向传播过程相同,遍历场中所有节点即可完成场的计算。针对本文中采用的三层神经网络结构,程序依据以下公式计算实现网络预测过程,

其中,ɑ为网络的输入值,w,v,b,γ 分别为输入层、 隐藏层的神经元权重和偏置量,σ代表激活函数,S为隐含层的输出,L表示网络的最终输出值。需要注意的是,网络的输入和输出均为经过Z-Score标准化后的数据,因此需要利用表中各组分的均值、方差信息来还原实际值。通过求解Z和Yc的输运方程,得到查表标量Z 和Yc,结合神经网络预测模块,即可得到显焓、组分质量分数及ώYc。
3
算例验证

为验证annReactingFoam对层流非预混火焰的模拟精度,本文将得到的解与直接求解详细化学反应方法得到的解进行了对比。采用OpenFOAM自带的surfaces后处理工具提取截面的VTK格式数据,采用Python程序转换为numpy矩阵后基于matplotlib工具生成标量分布云图。图8中给出了求解详细化学反应得到的解(Detailed)与annReactingFoam得到的解(ANNs)其温度及CO2质量分数的分布云图的对比。可以看出,两者的分布趋势基本一致,对温度分布的预测在火焰下游存在一定误差,该误差是由火焰面模型对该二维火焰结构的还原精度局限造成的。


采用OpenFOAM自带的singleGraph后处理工具提取火焰中轴线上的数据信息,并基于matplotlib绘制中轴线上的温度及CO2质量分数分布对比曲线。图9中可以看出,两组解得到的中轴线上的温度及CO2质量分数分布基本一致,在火焰上游处非常接近,而在下游处开始出现一定的偏差。
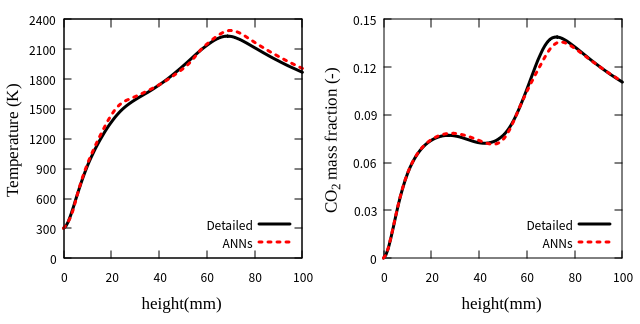
从以上对比可以看出,基于神经网络算法的annReactingFoam对层流非预混火焰的模拟可以达到接近于直接求解详细化学反应解的较高精度。
4
结论
1)annReactingFoam求解器可基于双参数火焰面模型实现对层流非预混火焰的模拟,层流轴对称伴流非预混甲烷/空气火焰的模拟结果与求解详细化学反应得到的解较为吻合。
2)通过本文的研究,验证了人工神经网络方法在层流非预混火焰燃烧模拟计算中的有效性、准确性,对后续的研究具有一定参考价值。
参考文献
[1] 陆阳. 燃烧计算中火焰面模型的研究[D]: 中国科学技术大学, 2009.
[2] Emami M D, Fard A E. Laminar flamelet modeling of a turbulent CH4/H2/N2 jet diffusion flame using artificial neural networks[J]. Applied Mathematical Modelling, 2012, 36(5): 2082-2093.
[3] Sen B A, Menon S. Turbulent premixed flame modeling using artificial neural networks based chemical kinetics[J]. Proceedings of the Combustion Institute, 2009, 32(1): 1605-1611.
[4] 周志华, 机器学习, 清华大学出版社, 2016.
[5] Nielsen M A. Neural networks and deep learning[M]. San Francisco, CA, USA:: Determination press, 2015.
[6] Jasak H, Jemcov A, Tukovic Z. OpenFOAM: A C++ library for complex physics simulations[C]//International workshop on coupled methods in numerical dynamics. IUC Dubrovnik Croatia, 2007, 1000: 1-20.
[7] Kee R J, Rupley F M, Meeks E, et al. CHEMKIN-III: A FORTRAN chemical kinetics package for the analysis of gas-phase chemical and plasma kinetics[R]. Sandia National Labs., Livermore, CA (United States), 1996.
[8] Chollet F. Keras: The python deep learning library[J]. Astrophysics Source Code Library, 2018.
[9] Pierce CD, Moin P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion[J]. Journal of Fluid Mechanics, 2004,504: 73-97.
[10] Claramunt K, Consul R, Carbonell D, et al. Analysis of the laminar flamelet concept for nonpremixed laminar flames[J]. Combustion and Flame, 2006, 145(4): 845-862.




