涡结构提取
Vortex is the tendon of fluid movement.
——Dietrich Küchemann


通过流线的封闭来显示涡的结构也是一种常见方法,比如:
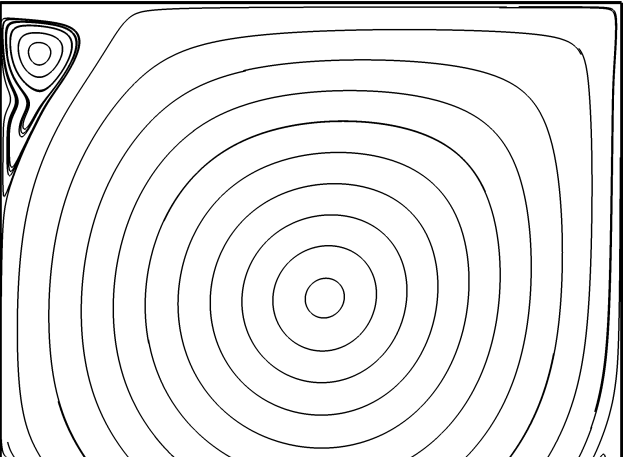
用涡量的模来显示涡结构是一种很常用的方法,类似下图:
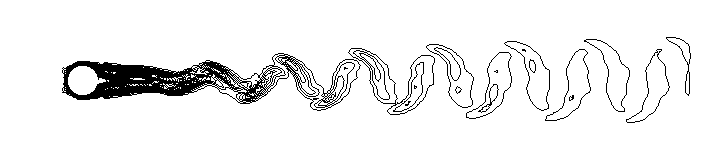 这种方法在自由剪切流中很有效,不过,对于壁面束缚流动则不太适用,原因是背景流动的剪切性导致的涡量模可以达到跟涡结构处的涡量的模差不多大小,这就使得涡结构难以从背景流动中分离出来了。并且,涡量的模的最大值通常发生在壁面上,而涡的核心显然不可能出现在壁面上。所以这种方法不适合用于提取边界层附近的涡结构。
这种方法在自由剪切流中很有效,不过,对于壁面束缚流动则不太适用,原因是背景流动的剪切性导致的涡量模可以达到跟涡结构处的涡量的模差不多大小,这就使得涡结构难以从背景流动中分离出来了。并且,涡量的模的最大值通常发生在壁面上,而涡的核心显然不可能出现在壁面上。所以这种方法不适合用于提取边界层附近的涡结构。
OpenFOAM 中提供了两种方法来提取涡结构:Q 和 Lambda2。
速度梯度张量的二阶不变量
速度梯度 的二阶不变量Q的定义为:
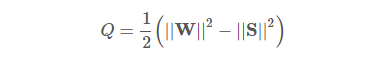
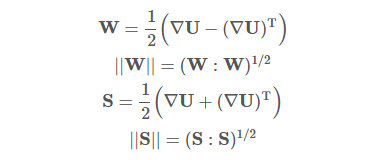
可以用Q>0 来作为涡结构存在的盘踞。
在OpenFOAM中,有一个程序用来计算Q,名字就叫Q。在流场计算完毕以后,可以运行Q,然后在 paraview 中显示Q值大于0的等值面来显示涡的结构。只是,OpenFOAM 中Q的计算用的是另一种方法:
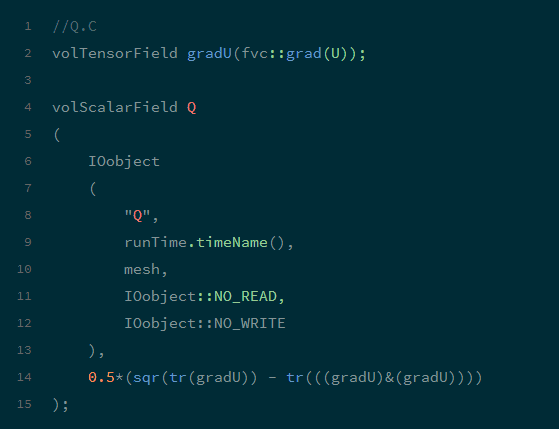
代码里注释说这是另一种计算 的方法,与上面公式的计算方法差别很小。
的第二大特征值
在 OpenFOAM 中有一个程序用来计算 λ2: Lambda2
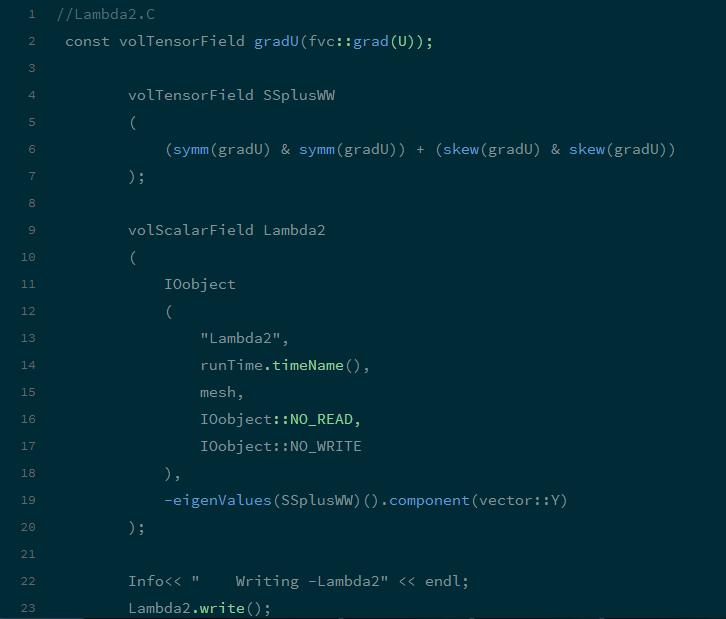
注意,OpenFOAM 返回的是-,所以,在计算了 Lambda2 后,需要通过 Lambda2 大于 0 的等值面来显示涡结构。本篇开头第一张图片,显示的是圆柱绕流的 Lambda2 = 500 等值面。
【参考】
来源 | http://xiaopingqiu.github.io
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-06-23
最近编辑:1年前
还没有评论
相关推荐
热门文章




