CFD中的预处理方法
新型冠状病毒肺炎疫情仍在持续,全国上下正在有序开展防控工作,疫情当前,减少外出活动、做好个人防护、远离人群是最好的预防手段。宅在家的这段时间也是充电的好时机,大家可以系统梳理、学习CFD,以下主要分享CFD中的预处理方法,欢迎留言交流~
为什么需要预处理?
一般的,如果一个矩阵的条件数非常大,那么它是病态的,或者刚性的。对于刚性或者病态系统,除了改变系统本身的条件数,没有其它特别奏效的数值方法。尽管本质相同,我们还是可以粗略的把刚性/病态问题分为两类。一类是微/积分方程组的刚性问题,另外一类则是针对一个特定的代数方程组。低速时的可压缩控制方程属于第一类,通常用的共轭梯度方法往往需要配合预处理才能有效的求解病态的代数方程组,这是第二类。
一 个 例 子

控制可压缩流动的Euler方程组(以下简称Euler方程组)可以简写为如下的形式

这里假设流动是一维定常的,τ 是伪时间(pseudo-time)。其中Q = (ρ, ρu, ρE)是守恒变量, F = (ρ,ρuu+p, ρuE)是对应的通量,E是总能。将该方程改写为拟线性的形式:

其中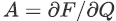 是Jacobi矩阵,三个特征值分别是v+c, v-c, v。其条件数:
是Jacobi矩阵,三个特征值分别是v+c, v-c, v。其条件数:
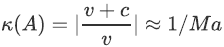
可见流动的速度越小 ,条件数越大,那么Euler方程组越发病态。
,条件数越大,那么Euler方程组越发病态。
观察一维定常Euler方程(1),人们只关心最后的定常解,对于求解中间过程是否对应真实物理,并不关心。当流动趋近于真实的定常解时,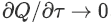 。
。


其中,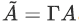 。
。
 ,那么我们要求解的方程(3)不再「病态」,是一个「好方程」了。必须说明,预处理方法破坏了原方程组的特征值,因此中间过程没有物理意义,不能直接用于求解非定常问题。不过,幸运的是,借助A. Jameson提出的双时间步方法[2],上述预处理方法稍加改进,即可应用于非定常问题的求解。
,那么我们要求解的方程(3)不再「病态」,是一个「好方程」了。必须说明,预处理方法破坏了原方程组的特征值,因此中间过程没有物理意义,不能直接用于求解非定常问题。不过,幸运的是,借助A. Jameson提出的双时间步方法[2],上述预处理方法稍加改进,即可应用于非定常问题的求解。这里仅以一维无粘Euler方程为例,实际的三维粘性可压缩NS方程在细节的处理上会繁琐很多,但预处理方法的原理是通用的。从数值求解的角度,一个可压缩求解器添加预处理模块并不困难,将方程(1)中的矩阵A替换为方程(3)中的 即可,即只需修改数值通量部分。
即可,即只需修改数值通量部分。
相 关 应 用

图1 二维Bump构型的数值模拟结果:等压线图,Ma=0.01,均使用ASUM格式。(a)无预处理;(b)预处理。

图2 预处理后的残值收敛历史[6]
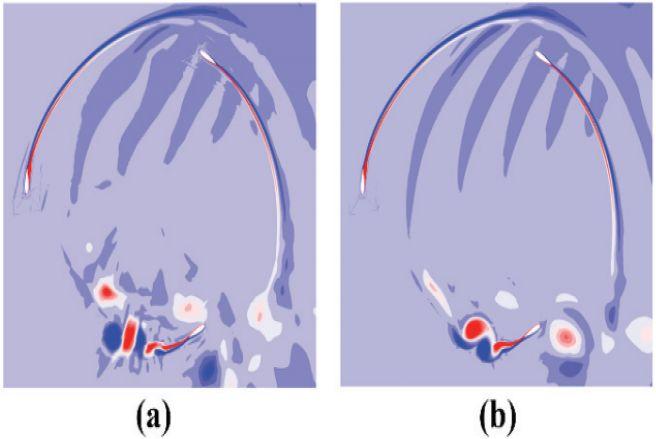
图3 涡量云图[7] (a)无预处理;(b)预处理。
延 伸
多物理场耦合问题[4]。多物理场,也必然是多尺度的,如MHD问题[3]。
燃烧问题。燃烧过程诸多化学反应的特征尺度,通常会跨越多个数量级。
一般来说,代数方程组的规模越大,条件数也随之急剧增加,比如Laplace/Poisson方程。Krylov子空间方法在现代CFD中非常受欢迎,但在求解大规模代数方程组时,也必须结合预处理方法。
...
预处理方法原理虽然简单,但面对特定问题,如何给出最优的预处理矩阵?这需要学者对该问题具有非常深刻的物理洞见。针对交叉学科具体问题的预处理方法依然是现代CFD研究的一个核心课题。
参考文献
[1] Turkel E. Preconditioning techniques in computational fluid dynamics[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 385-416.
[2] Jameson A, Schmidt W, Turkel E. Numerical solution of the Euler equations by finite volume methods using Runge Kutta time stepping schemes[C], 14th fluid and plasma dynamics conference. 1981: 1259.
[3] Ma Y, Hu K, Hu X, et al. Robust preconditioners for incompressible MHD models[J]. Journal of Computational Physics, 2016, 316: 721-746.
[4] Ferronato M, Franceschini A, Janna C, et al. A general preconditioning framework for coupled multiphysics problems with application to contact-and poro-mechanics[J]. Journal of Computational Physics, 2019, 398: 108887.
[5] Weiss J M, Smith W A. Preconditioning applied to variable and constant density flows[J]. AIAA journal, 1995, 33(11): 2050-2057.
[6] Han Z, He F, Song W, et al. A preconditioned multigrid method for efficient simulation of three-dimensional compressible and incompressible flows[J]. Chinese Journal of Aeronautics, 2007, 20(4): 289-296.
[7] Campobasso M S, Yan M, Bonfiglioli A, et al. Low-speed preconditioning for strongly coupled integration of Reynolds-averaged Navier–Stokes equations and two-equation turbulence models[J]. Aerospace Science and Technology, 2018, 77: 286-298.





