液体火箭发动机燃烧仿真的若干问题
液体火箭发动机燃烧仿真比较大的问题是缺乏直接的实验测量数据进行验证。目前直接的测量数据只有壁面温度,壁面热流密度,室压和比冲等少量数据。
01
微尺度流动模型
微尺度效应可以归纳为表面效应,非连续介质效应,低雷诺数效应和多尺度效应等。对于发动机微尺度范围0.01-1mm内的流动燃烧问题,不能再继续使用连续介质模型;且热力学平衡条件亦往往不再成立。
流动机制 | Kn数范围 |
无滑移流动机制 | Kn<0.001 |
滑移流动机制 | 0.001<Kn<0.1 |
过渡流动机制 | 0.1<Kn<10 |
自由分子流动机制 | Kn>10 |
对于滑移流来说,求解滑移边界条件下的NS方程,是目前滑移流区普遍采取的方法。滑移边界的提法,按阶数有一阶以及多阶之分。且有研究表明,二阶的滑移边界条件在增加模拟精度不太明显的时候,增大了模拟难度与计算量以及收敛时间。在多年的研究中,一阶滑移条件有三种主要的形式:Maxwell滑移条件、Gokcen滑移条件、Lockerby滑移条件[1] 。
当气体流动进入过渡领域,基于连续性假设的NS方程即不再适用,即便是在滑移边界条件下,往往亦不够准确。在近壁面处的气体流动需考虑速度滑移、温度跳跃等情况,仅凭传统的CFD方法已经无法满足要求。进入微观领域,多孔介质的边缘与内部往往广泛分布着微小的凸起与裂缝,从毫米级、微米级,甚至到纳米级不等,加之局部区域存在流动通道变窄或变宽等情况。在该流动领域内,目前采用如下方法进行计算:
1.DSMC;
2.DSMC与CFD耦合;
此外,有研究人员采用NS方程配合二阶速度滑移条件对部分过渡流区域的流动(Kn~0.8)进行了计算,并将其计算结果与DSMC以及实验数据进行了比较,得到了误差可以接受的结果[2] [3]。
02
传热模型

图1 燃烧室气流图
常用的辐射换热模拟主要有:热流法、区域法、蒙特卡罗法、离散传递法和离散坐标法。其中应用的较为广泛的是区域法。当分区的数目不太多时,该方法有很好的计算精度。使用该方法最重要的就是计算每两个区域之间的定向辐射交换面积。这其中要计算多个重积分,比较昂贵。
03
雾化机理与模型
对于液体推进剂的雾化机理,前人做过大量研究。首先较为简单的就是静态液滴形成的机理,其液滴大小受到表面张力和重力而共同决定。
其次是关于圆柱射流破碎的研究。19世纪末到20世纪末国外科学家进行了大量研究,以Ohesorge与Reitz等人的研究成果为代表,将圆柱射流的破碎按照Re数和Oh数的变化给出了分区图,定性估算了每类破碎情形产生的液滴直径与射流直径的关系[4] 。对于单孔喷嘴的初次雾化,一般可采用Blob模型。
公 众号:诺丁汉大学工程学院
以上介绍的都是射流或者液膜的一次破碎过程。在进入相对高速的气流中,如果液滴周围的气动压力大于液滴的表面张力,那么液滴就会发生二次破碎。
对于液滴在层流气流中的二次破碎,Hinze认为取决于气动力、表面张力与液体粘性力三种力的共同作用效果。此外,考虑环境气体粘性时,控制液滴破碎的主要因素是粘性剪切力和液滴表面张力。目前已有成熟的模型,如TAB模型、Reitz-Diwakar模型、KHRT模型、SSD模型等[5] 。
对于射流的雾化仿真,近年来普遍采用LES甚至是DNS方法进行研究。Menard等对初次雾化进行了3D DNS计算[6] 。Plateau-Rayleigh不稳定性使得流动的水柱最终断裂形成水滴。Ding等采用VOF和LES方法对空心锥形旋流喷雾的初次雾化进行了模拟[7]。Lebas等采用Eulerian-LagrangianSpray Atomization model (ELSA)与RANS模型对射流水柱的初次雾化与二次雾化进行了模拟[8] 。
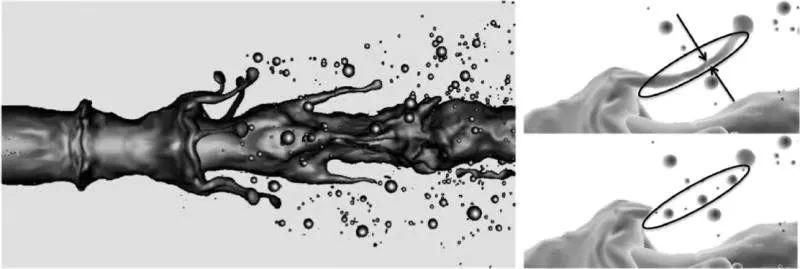
图2 射流雾化[16]
高压喷射过程中,喷嘴内部的流动状态往往是与空化过程密切相关的。目前主流的空化模型有如下三种:Singhal模型,Zwart-Gerber-Belamri模型以及Schnerr-Sauer模型。

上海积鼎信息科技有限公司为行业用户开发的一款模拟管道内空化流的求解器,采用的是可压缩的漂移流混合物模型,空化模型是Singhal模型以及Schnerr-Sauer模型。因为压力跨度较大,工质水的状态方程采用的是Peng-Robinson方程,其计算得到的临界质量流量与实验结果对比误差范围在7-9%。
04
湍流燃烧模型
现今,双组元液体火箭发动机已被广泛应用于航天飞机、卫星等多种空间飞行器中,其主要功能是为飞行器的轨道控制和姿态控制提供动力。双组元液体火箭发动机燃烧过程的数值模拟现阶段的难点主要集中在以下两方面:
首先,双组元液体火箭发动机内的燃烧过程复杂,涉及多相流、传热、燃烧等多种物理化学现象及其之间的耦合作用,需要选择合适的模型描述以上多种过程;
其次,推进剂燃烧温度高,为防止燃烧室内壁过热,通常采用液膜冷却的方式,如何准确模拟液膜的动态发展过程以及推进剂液滴与液膜间的相互作用成为研究的难点之一。
针对以上关键科学问题,国内外研究学者们开展了大量研究工作。国外的数值仿真工作开展较早,许多燃烧模型已被提出并被应用到成熟的程序中。
法国国家航空航天研究中心(ONERA)开发了模拟液体火箭发动机燃烧过程的PHEDRE软件[13] ,ONERA基于该软件研究分析Viking型液体火箭发动机燃烧的不稳定性问题。
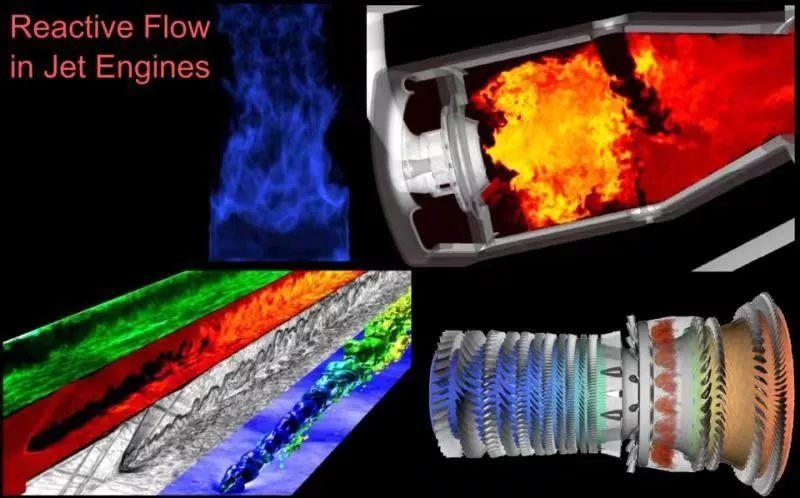
图3 湍流燃烧[16]
参考文献
[1] Lockerby D A. Geometric and Constitutive Dependence of Maxwell's Velocity Slip Boundary Condition [R] ADA Report, 2005.
[2] Jean Maurer, Patrick Tabeling, Pierre Joseph, and Herve Willaime,Second-order slip laws in microchannels for helium and nitrogen,Physics of Fluids 15, 2613 (2003)
[3] 谢翀, 樊菁,Navier Stokes方程二阶速度滑移边界条件的检验,力学学报,第39卷第1期,page 1-6,2007
[4] 王振国,液体火箭发动机燃烧过程建模与数值仿真,北京:国防工业出版社(2012)
[5] ANSYS Fluent Theory Guide, Release 16, ANSYS, Inc. 2015
[6] Menard T, Tanguy S, Berlemont A, Coupling level set/VOF/ghost fluid methods: Validation and application to 3D simulation of the primary break-up of a liquid jet. International Journal of Multiphase Flow 33 (2007) 510-524
[7] Ding J.W., Li G.X., Yu Y.S., and Li. H.M., Numerical Investigation on Primary Atomization Mechanism of Hollow Cone Swirling Sprays, International Journal of Rotating Machinery, Volume 2016, Article ID 1201497
[8] Lebas R, Menard T, Beau P.A., Berlemont A, Demoulin F.X., Numerical simulation of primary break-up and atomization: DNS and modelling study. International Journal of Multiphase Flow 35 (2009) 247-260
[9] O’Rourke P. J. A Particle Numerical Model for Wall Film Dynamics in Port-Fuel Injected Engines [J]. SAE Fuels and Lubricants Meeting Paper. 1996, 961001-1: 1-16.
[10] Knab O, Preclik D, Estublier D. Flow field prediction within liquid film cooled combustion chambers of storable bi-propellant rocket engines[C]. 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. 1998: 3370.
[11] Preclik D, Estublier D and Wennerberg D. An Eulerian-Lagrangian Approach to Spray Combustion Modeling for Liquid Bi-propellant Rocket Motors[R].AIAA 95-2779
[12] Knab O, Frohlich A, and Wennerberg D. Design Support for Advanced Storable Propellant Engines by ROCFLAM Analyse [R].AIAA 99-2459
[13] Habiballah M, Lourme D, Pit F. PHEDRE-Numerical model for combustion stability studies applied tothe Ariane Viking engine[J]. Journal of Propulsion and Power, 1991, 7(3): 322-329.
[14] Catoire L, Chaumeix N, Paillard C. Chemical Kinetic Model for Monomethylhydrazine/Nitrogen Tetroxide Gas Phase Combustion and Hypergolic Ignition[J]. Journal of propulsion and power, 2004, 20(1): 87-92.
[15] Ohminami K, Ogawa H, UESUGI K. Numerical Bipropellant Thruster Simulation with Hydrazine and NTO Reduced Kinetic Reaction Model[C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. 2009: 452.
[16] https://web.stanford.edu/group/fpc/cgi-bin/fpcwiki/Main/Gallery





