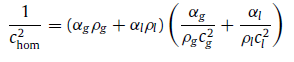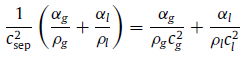气液两相流声速的直接数值模拟
飞行器速度接近音速时,飞行器前面的空气来不及恢复原状,一直处于压缩状态,不断叠加后阻力急剧增大,使飞行器产生强烈振荡、速度衰减,甚至会导致飞行器失控,这使得前人们一度以为音速是飞机速度不可逾越的障碍,被称之为音障。
突破音障时,由于飞行器本身对空气的压缩无法迅速传播,逐渐在其迎风面积累,形成激波面,在激波面上声学能量高度集中。激波面后方(post shock)压力升高,该压力超过常温条件下的饱和蒸汽压,引起空气中水蒸气雾化,也就是飞行器机翼附近出现的凝结雾。
在流体力学中,流体随压强的增大而体积缩小的性质,称为流体的压缩性。以上现象归根结底都是流体的可压缩性引起的。

在多相流中,即使是常态下的不可压缩流体,在一些条件下其可压缩性依然不可忽视。例如管道系统在极端条件下会产生阻塞流、水锤等流体压缩现象,对管道系统的质量输送、管壁的稳定性产生影响,也是实际工程安全中需要考虑的问题。
空气动力学中,常常会提及马赫数。马赫数为物体速度与当地音速的比值大小,本质上体现流体被压缩的状态。流体的可压缩性通常借助马赫数进行判断,那么流体中的声速的计算就显得格外重要。 汽液两相流表现出很多与单相流不同的性质。如汽液两相流体中的音速远低于其中任何一种单相流体,当截面气含率在50%时,其音速仅为几十米每秒。如此低的音速使两相流体很容易实现超音速流动。超音速流动在受到干扰或背压影响的情况下可能发生激波,激波的发生将使两相压力突增,增加两相的化学势差,促进相变的发生。
在一维单相流情境下,流体密度的变化与流动速度的变化可由下式描述: 
其中,M为马赫数。当M值较小时,流体可视作不可压缩状态;随着流速的增加,流体的密度逐渐减小,而当M=1时(即流速达到声速),质量通量ρu将达到最大值,此时的流速即称为临界流速(critical flowvelocity)。 实际上,而对于管道内存在气液两相流的条件下,情况与单相流又大为不同。以下给出了在两种不同流型的两相流中的当地声速的理论解:
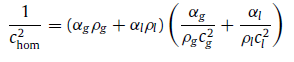
分层流中可以观察到明显的气液交界面,一般上层为密度较小的气相,下层为密度较大的液相: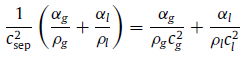
在Chang & Liou提出的分层流模型(stratified flowmodel)计算两相流问题的基础上,对离散两相流下的声速问题进行了直接数值模拟(最小网格尺度为5微米)。分层流模型中,通过体积分数在网格面上的重构,将网格面上的通量分为两侧分别是气体-气体,气体-液体和液体-液体这三种情况。
时间积分采用4步Runge-Kutta方法,空间离散则采用3阶Osher-Chakravarthy TVD格式。
对标的实验工况中,气泡直径为0.1mm。数值模拟中,过粗的网格在一定程度上会影响计算结果的准确度,而精细的网格又会增加计算量。为了提高计算精度并兼顾计算量,首先需要选定合适的网格尺寸。 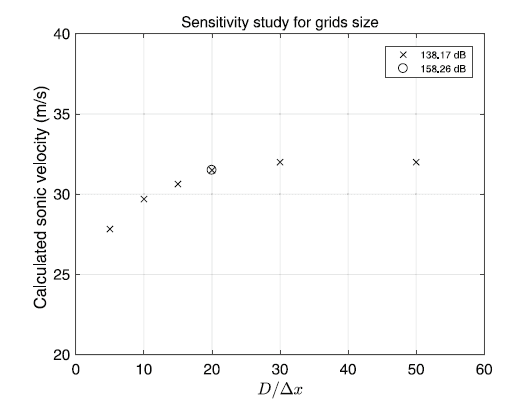
图1 网格无关性测试结果
可以看出,当气泡直径(D)比网格尺度(Δx)等于20时,计算得到的声速大小基本不变,计算达到收敛。另外也可以看出声速与扰动强度无关。
2 两相混合流的声速计算
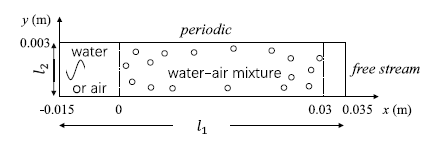
图2 两相混合流2D计算域设置简图
左侧入口为压力扰动边界,右侧为自由流动边界,上下侧均为周期边界,计算域中部的气相混掺区域设置直径大小均一致的气泡/水滴,该颗粒的直径约0.1mm。压力扰动将从左侧向右传播,经过两相混合区域,并从右侧传出。
对于一个典型的工况DNS计算,网格量约400万,时间步长约7E-10s(CFL=0.2),采用900多核并行计算了约4天。图3为受压力扰动(压力云图的legend测量区间[-10Pa,10Pa])的二维掺气泡两相压力云图。 
图3 受压力扰动的二维掺气泡两相压力云图
图4给出了在常温常压下,扰动频率f=10kHz,D=0.15mm情况下的声速计算的仿真、实验值及理论解之间的对比。理论解给出的是分散均匀流以及分层流的理想条件下的声速值,而仿真模拟及实验结果实际上是介于这两种理想条件之间的。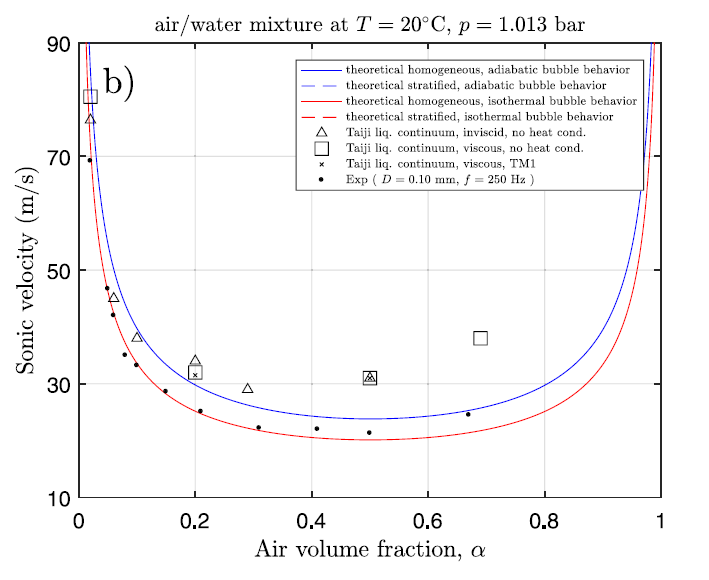
图4 离散的气液两相流声速随气含率的变化
由图4可以看出总体仿真得到的声速结果与实验结果较吻合,出现的部分差异认为是由于仿真与实验中的扰动频率不一致造成的。仿真中的扰动频率f=10kHz,而实验中的扰动频率f=250Hz。值得注意的是,当相分数取0.5时,当地音速达到最小值约30m/s。
采用分层流模型对空气-水两相流中的压力传播过程进行了直接数值模拟。通过与实验和理论解的对比,验证了本方法在计算两相流声速方面的准确性。同时,研究中发现当气含率α=0.5时,当地音速达到最小值。
两相流中的声速大小与两相流流型是密切相关的。据此,可通过测量两相流中的声速判断内部的两相流的流型。从这点上来讲,以上工作为两相流流型的判断提供了一种思路。