VirtualFlow | 射流反应器中湍流的LES预测验证
这里使用通用流体仿真软件VirtualFlow,LES方法模拟CIJR的内部流动。
工况及边界条件
CIJR的模型如下图所示,其包括一个圆柱形的反应室和圆管作为进出口。流体通过两个相对的直径 为1mm的圆管,以平均流速uj进入反应器,而后从底部直径为2mm的圆形出口流出。反应器圆柱体直径为D=4.8mm. 反应器总容积约为V=1.73×10-7m3, 小容积意味着流体的平均驻留时间很短。
为1mm的圆管,以平均流速uj进入反应器,而后从底部直径为2mm的圆形出口流出。反应器圆柱体直径为D=4.8mm. 反应器总容积约为V=1.73×10-7m3, 小容积意味着流体的平均驻留时间很短。

图1 CIJR模型
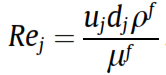
 (选择该流体是因为其折射率与反应容器壁的折射率更为匹配)。此处研究了5个不同流率下对应不同流速uj,驻留时间
(选择该流体是因为其折射率与反应容器壁的折射率更为匹配)。此处研究了5个不同流率下对应不同流速uj,驻留时间 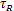 和雷诺数Rej见下表。
和雷诺数Rej见下表。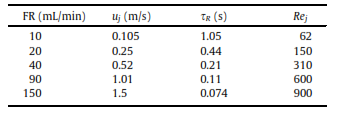
计算域网格见下图。
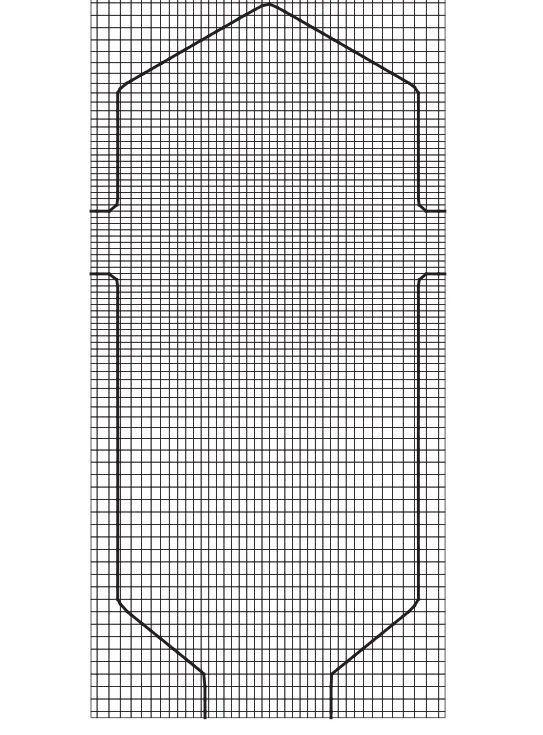
图2 网格划分
模 拟 结 果
1 瞬时流动
图3与图4展示了FR=90mL/min 时不同进口条件下反应器内部瞬时速度场分布。
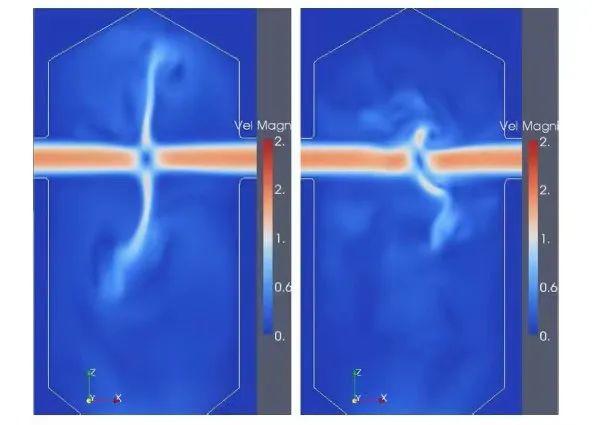
图3
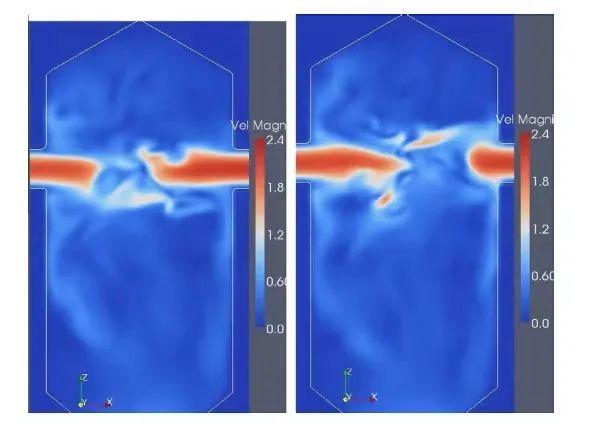
图4
左图的模拟对应恒定进口流率等于标定流率,可以看到容器内部速度出现了大尺度的脉动;右图的模拟对应更符合实际情况的震荡进口流率,可以看到反对称的速度进口条件带出了更多尺度的速度脉动,这些脉动在恒定进口流率的情况下即使加密网格也不能观测的到。
这些不同尺度的流动结构在图5的涡旋大小的分布图中更容易看出。涡量可以很好的反映出流动的结构、生成与耗散的尺度和它们与当地剪切流的相互作用。
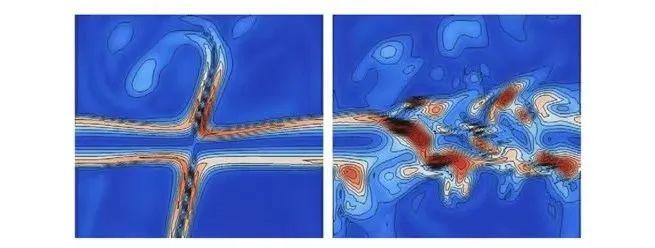
图5
对于流场中物理量与实验的对比,这里数据采集于射流撞击点附近的进入口轴线。轴线周围正是最重要的物理现象发生的位置。
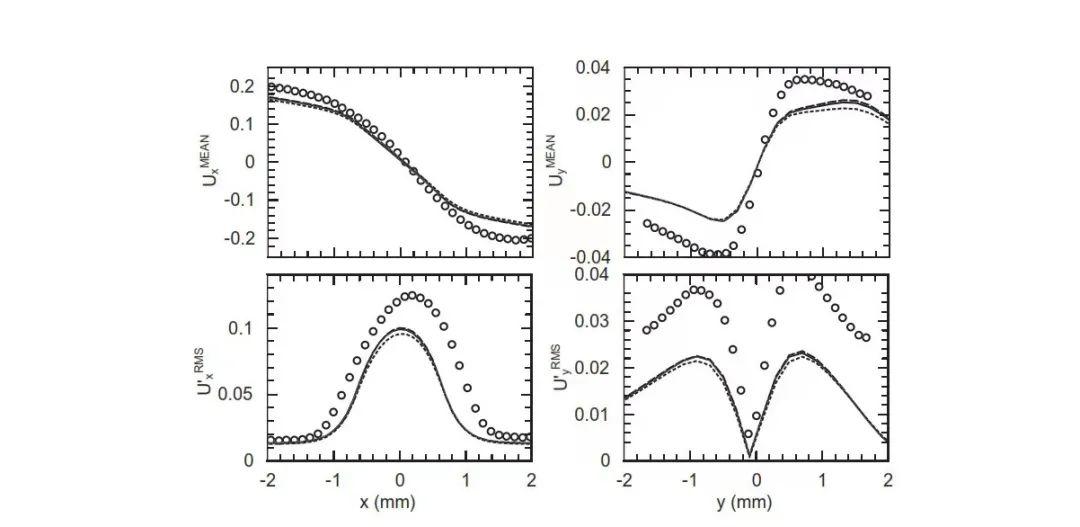
图6
LES分别采用“constantSGS”模型加HLPA格式 (图中实线) 、“constant Smagorinsky ” 模型加QUICK格式 (图中虚线) 和Germano的 “dynamicSGS model” 模型加HLPA格式 (图中点划线)。
这三种模型以及数值格式在图中并没有显著差异,因为在此低流率下容器内部流动比较均匀。在与实验数据 (图中圆点) 进行对比时,LES能够近似得到一阶量(如时均速度) 和二阶量 (如速度脉动的均方根)。
当进口速度流率增加时,更多流体的非定常特征出现,微弱的湍流特征也开始出现,尤其是中等流率 (FR=20-40 mL/min )下,内部流动开始自发地震荡,但是速度波动的幅度与位置在恒定进口流率下并不能被捕捉到。这些工况下,流动进入转捩区,包含能量的级串 (the energy-containing cascade) 并未完全发展,这导致模拟预测结果没有那么准确。
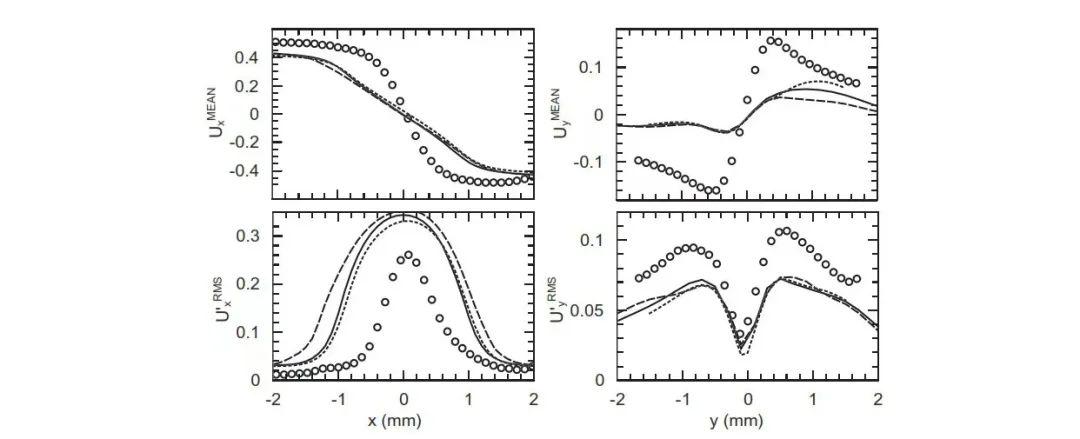
图7
图7模拟预测的结果与流率FR=20mL/min的实验数据进行对比。尽管计算所得速度脉动值在x方向上偏高,进而导致冲击平面上的大速度脉动和x=0处的y速度分量偏低,但总体的特征已经被描述到位。该流率下,在刻画沿x方向上的速度脉动方面,HLPA与QUICK格式下的计算结果差异更为明显, QUICK格式相对而言数值耗散更小些。
当流率大于40mL/min时,实验数据的不确定性开始越来越明显。这部分归结于容器的曲线外形和容器的小尺寸,刚好将观测平面置于容器中间变得十分困难。
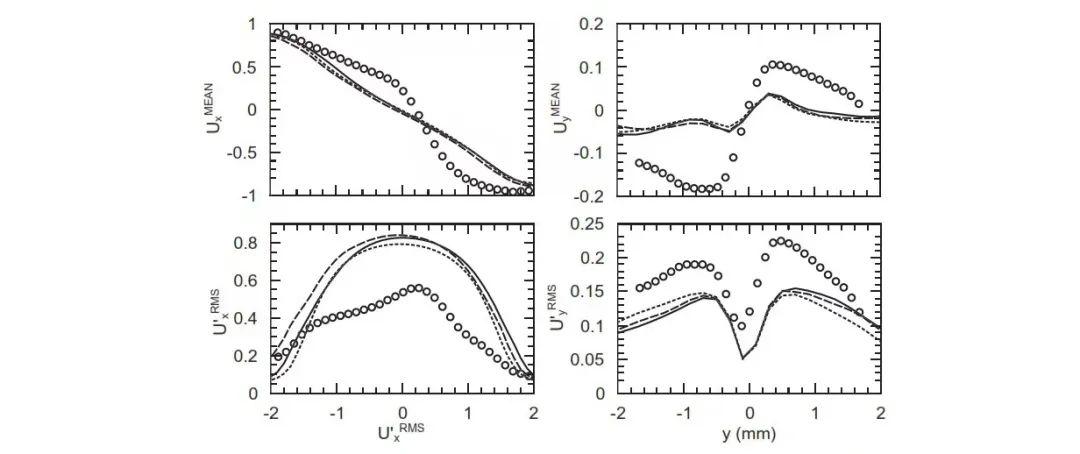
图8为流率FR=40mL/min下的计算结果。速度脉动的均方根RMS略微偏高,而时均速度与实验数据吻合得更好。这可能是由于边界条件的脉动近似突出了撞击流的不稳定性。流率为90mL/min的算例中,流体已接近充分发展的湍流,LES可以很好地模拟出速度x分量的光滑分布和x轴上的大速度脉动。同样的,y方向上的速度分量 (包括时均速度和脉动的均方根)也吻合得很好。
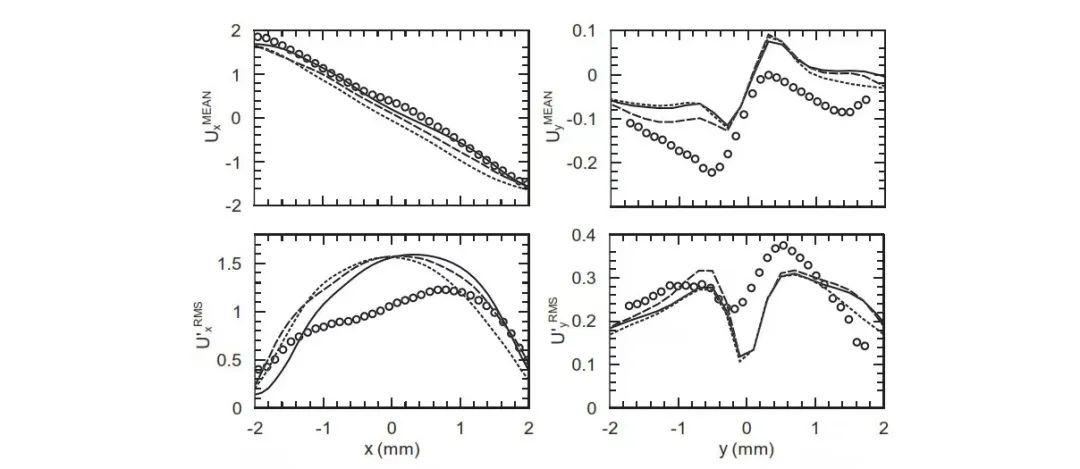
对于高流率而言,速度在y方向上的分布对射流对齐度,对称度和震荡十分敏感,因为除去射流撞击点,y方向上的分速度和x方向上的分速度相比总是很小。因而y方向上分速度不能每次被预测得准确,这正是由于射流撞击产生的速度脉动会被略微高估。x轴上的y方向上的速度脉动与撞击点x=0相比更为分散。然而这种效应并不会对总体的湍流流动和反应器内部的混合效率产生很大的影响。
总体而言,由于VirtualFlow软件生成的网格质量较高,数值格式的差异对模拟预测结果没有明显影响。相比而言,SGS模型的选取往往更为重要,但是此算例中SGS模型预测出的结果之间差异也很小,这说明对于此几何和工况,constant Smagorinsky 模型已经足够。另外,模拟的流场的湍流特性不仅与射流的撞击有关,还与非定常的进口流率相关。这说明,模拟与实验的差异很可能不是由于SGS模型的不足或者数值问题,而往往是因为采用的速度进口边界条件与实际不符,因此真实工况的模拟尤其重要。




