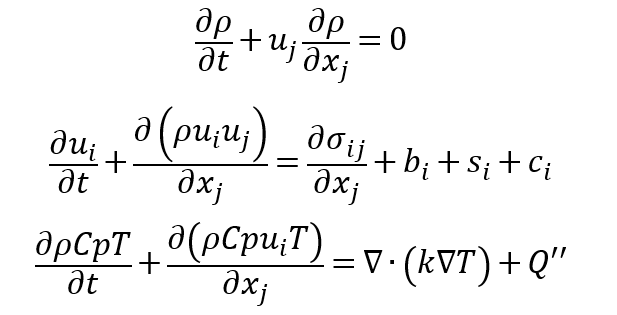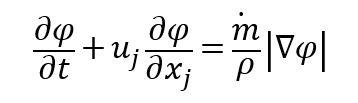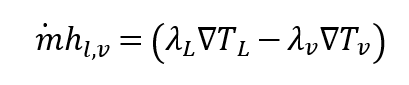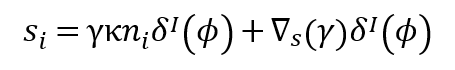VirtualFlow │ 界面跟踪技术的气泡成核与传热CFD数值仿真
沸腾在各种工业过程中具有巨大的重要性,尤其在冷却与核电领域。成核沸腾可能是众多快速散热手段中最有效的方法,这使得其在高密度电力电子设备的热管理中具有广阔的应用前景。
沸腾作为一种复杂的两相流动现象,存在多个动态演化的界面。同时,沸腾过程覆盖了广泛的长度尺度,甚至延伸到分子水平。尤为重要的是发生在加热器表面的传热机制,对加热器表面的传热机理的研究,长期以来仅限于积分测量或单点测量(即表面平均热流密度和温度,以及局部温度)。
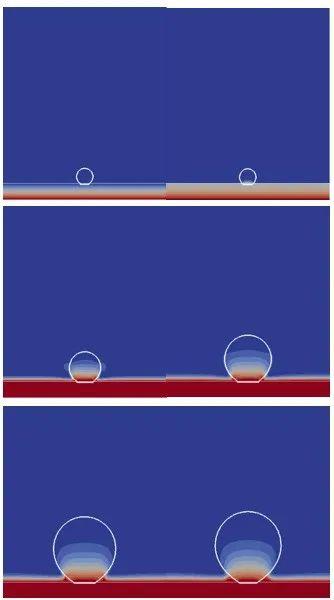
BETA-B的实验结果(图1)表明,在高热通量时,蒸汽反冲力比毛细力和重力更占优势。蓝色虚线环表示dam-breaking时的气泡(左上)、再润湿开始时(右上)和再润湿过程中的气泡形态(第二行)。这里基于二维轴对称模型对开放介质中在固壁表面发生单气泡生长、薄膜沸腾及气泡生长和脱离等过程进行数值模拟仿真。 单相流形式下的不可压缩流体动力学和传热方程为:
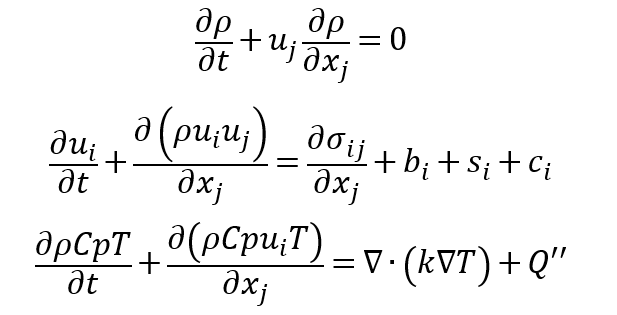
在Level-set方法中,相间界面用连续函数φ表示,φ表示到界面的距离,该距离一侧为正,另一侧为负:
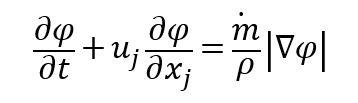
其中传质速率满足
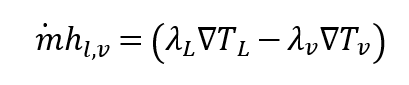
此外,φ作为跨界面的连续函数有助于确定界面的法向量,从而确定定义表面张力所需的表面曲率κ=-∇φ/|∇φ|,
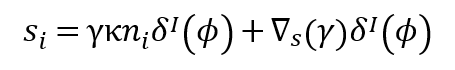
其中γ是流体的表面张力。引入上式的最后一项是为了模拟与温度或表面活性剂浓度引起的表面张力系数变化率有关的马兰戈尼效应。
这里在动量方程中增加了三线力,提供了对润湿表面的物理充分描述。在VirtualFlow中使用的三线力是基于对界面自由能的考虑,其只与两个参数流体有关:界面张力γ和平衡接触角θ:
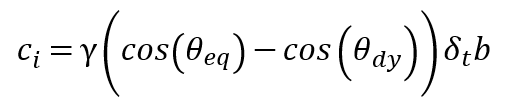
其中b是垂直于三线且平行于壁面的单位向量。
这里对无限大介质中蒸发气泡的传质速率进行了测试,在无限大介质中,传质速率不受限制,而直接由界面处的热流密度平衡计算得到。数值模拟在二维轴对称条件下进行,计算域尺寸为1.2×1.2mm,包含初始半径为0.1mm的四分之一气泡(二维轴对称模型)。数值模拟中,密度比为40,过热1K。网格分辨率:0.02mm和0.01mm笛卡尔单元。压力解收敛准则10^(-6),其他变量的收敛准则为10^(-4)。时间递进方案为三阶显式,具有基于CFL数的自适应时间步进,克朗数限制在0.1和0.2之间。特征速度为0.14米/秒。结果显示在图2的前两幅图像中。仿真结果与Mikic等人的解之间的一致性非常好,并且计算结果的跟随性随网格的细化而进一步增加。在0.01mm分辨率(蓝线)的传质率有下降是由于计算域尺寸有限的限制。此时气泡半径约为1mm,而计算域只有1.2mm。气泡周围的流体不再处于初始的过热温度状态,因此不能保持与Mikic等人的结果相似的增长率。 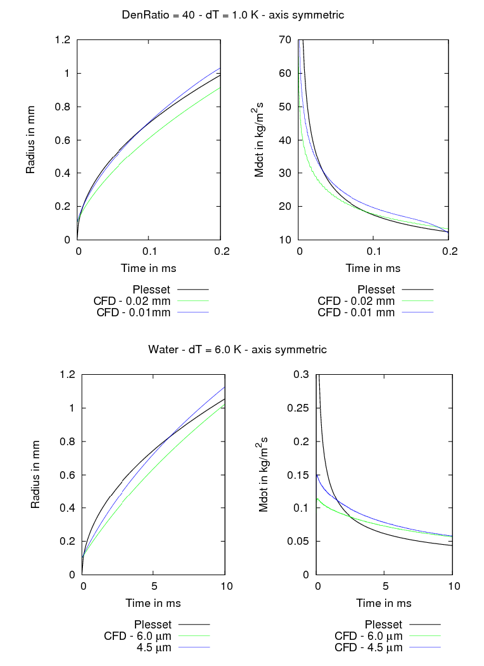
图2 模态沸腾验证:密度比为40的流体在1k过热(上)和水在6k过热(下)的计算结果
第二组模拟用水(密度比为900)进行。与第一组的情况有所不同,Welch等人的结果显示在温差为6K的情况下,分辨率分别为6.0µm和4.5µm。得到的Jakob数是17.94,比第一组大得多。这里限制CFL值的时间步长设置在0.5和0.8之间。图2中的下侧两幅图片展示了计算结果。模拟结果与Plesset解的一致程度不如模态沸腾,但气泡半径的一致程度较好。主要原因系初始阶段的传质率较难被精准捕捉。根据理论解,传质率依赖于时间成1/sqrt(t)关系,因此传质率在模拟初始阶段趋近于无穷大,所以无法被精确捕获。当然,如果使用更高分辨率的网格进行测试可以更好地预测传质速率,但需要大量的计算成本。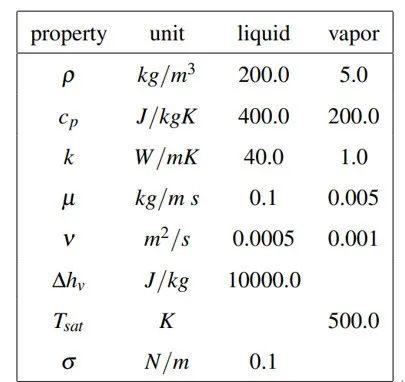
表1 膜态沸腾的流体特性
这里给出的验证算例中的流体性质如表1所示。计算域尺寸为λ×3λ,其中为最不稳定的泰勒波长。因此,计算域尺寸设置为0.078684m×0.226m,覆盖有64×192个单元格(图3)。上边界为压力出口,左右边界为周期边界,下边界为5K过热壁面,Jacob数为8.0。壁面附近的网格距离较小,用以分辨蒸汽薄膜。当气泡形成时,气泡薄膜的厚度会变窄,壁面附近的网格分辨率需要保证薄膜厚度至少大于一个网格的厚度。采用的最小网格尺寸为0.59mm。用基于最不稳定泰勒波长的薄膜厚度初始化计算域。液-汽界面设定为饱和温度。蒸汽区域初始化时在两相界面的饱和温度和壁面过热温度之间采用线性温度曲线过渡。对流项离散方案采用HLPA。压力的收敛准则为10^(-6),其他变量的收敛准则为10^(-4)。CFL数限制在0.2和0.3之间。工况的特征值与无量纲数为:l=2mm, u=0.14m/s, t=0.014s, Pe=0.56, Re=0.56, We=0.0784。
结果如图3所示。图3中的时间序列为:(自左上到右上,左下到右下分别为)0.42秒,1.3431秒,1.4207秒,1.4947秒,1.5734秒,1.6370秒。图3展示了一个准稳定气泡释放的完整周期。第二幅图片(上中)展示了处于气泡释放过程起点的情况,可以再次在第五(下中)和第六(下右)幅图片间某时刻重复出现。整个模拟过程显示出准稳态气泡释放模态下的三次气泡释放过程。三个周期的平均释放周期用时约为0.26s。
这里对在固壁表面沸腾的气核进行了数值仿真,气核中的传质速率是根据界面处热流密度平衡计算。数值模拟基于二维轴对称计算模型进行,计算区域尺寸为7mm×2.5mm,包含初始半径为0.25mm的四分之一气泡(二维轴对称模型)。对流项采用HLPA离散格式,对Level-set方程采用QUICK离散格式。液相与蒸汽的密度比约为1600,过热6.7K。采用单元尺寸为0.0267mm×0.0267mm的笛卡尔网格。隐式时间方案具有基于CFL数的自适应时间步进,CFL数限制在0.9和0.7之间。特征速度0.151米/秒,接触角38°。
计算域底部为固体固壁,密度8932.0kg/m^3,热容量为385J/kg-K,导热系数为401W/m-K,初始固壁底部过热6.7K,以模拟固体达到稳态温度时的共轭传热过程。由于壁温过高,液体与蒸汽之间的相变开始发生。图4第一行两幅图先显示,气泡在早期阶段的生长速度较慢。图4中第二行图像中气泡的半径变化显示,气泡的增长最初主要受界面传热的影响。图4第三行图像显示,随着浮力的影响变得显著,气泡的增长开始受到流体动力学的影响。图4第四行图像显示,由于周围液体的运动将气泡推得更高,气泡底部迅速收缩。图4最后一行图像显示,在气泡底部收缩后,气泡与固壁之间发生分离,当气泡离开时,其原本的位置被温度较低的液体占据。这意味着气泡的离开在下一个成核周期开始前改变了固壁表面流体中的温度分布情况。基于VirtualFlow中的浸没表面技术(IST)将传导传热和对流传热结合起来,这里给出了三种流动情景下的结果,并与解析解、实验结果及其他人的数值结果进行了对比验证,对比验证结果非常良好。通过研究处理涉及沸腾传热过程的具体情况,更全面地了解沸腾传热机制,同时开发出基于连续介质力学的CMFD宏观数值仿真模型,并搭载进入VirtualFlow计算平台,解决了针对沸腾传热传质过程的数值仿真难题。