同一个师父,同一个CFD
还记得当年在学校学习《数值传热学》的时候,老师拿出了帕坦卡经典的书籍《传热与流体流动的数值计算》并告诉大家:“感谢我的老师当年不远万里从明尼苏达大学带回来的这本教材还有帕坦卡的CFD思想,等到学完这门课程之后,你们就是帕坦卡的广义弟 子了。”
后来笔者也懵懵懂懂的开启了CFD之路,还知道了另外一个更加响亮的名字——斯伯丁,此人便是帕坦卡的导师,更是现代CFD的创始人。今天,我们就来聊聊这位师父的师父。
大神的三十而立
Brian Spalding
1923 年 1 月 9 日,布莱恩·斯伯丁(Brian Spalding)出生于伦敦郊区的小镇新莫尔登,这儿是一个环境优美的英国乡村。作为一个典型的学神,Spalding在求学路上也是一路开挂,18岁被牛津大学录取,并于1944年,获得皇后学院工程科学专业的学士学位。
本科毕业之后,Spalding在壳牌公司工作了一年。此时正值二战的末期,为了应对德国大名鼎鼎的V2导弹,英国航空部成立了全新的火箭推进机构。1945年,Spalding响应国家号召,投身祖国最需要的地方,加入了该机构并于战后被政府派往德国学(瓜)习(分)火箭技术。也正是在对火箭技术的研究中,Spalding开始接触燃烧和传热学。一年之后盟军达成了协议,不在德国本土开展火箭的研究工作。于是,Spalding等人回到英国,继续从事这项秘密的工作。
不久之后,英国政府重建了从事科研工作的公务员制度,或许是因为Spalding在学生时代的政治身份,导致Spalding从核心的火箭部门转移到了国家物理实验室 (NPL)的计量部门。如果不是这次的工作调动,这世上也许就少了一位CFD的大佬,而多了一个隐姓埋名的火箭科学家。
在国家物理实验室经历了短暂的停留,Spalding在1948年申请到了ICI奖学金,并进入剑桥大学攻读博士学位,因为之前在火箭推进部门的背景,Spalding还是将液体燃料的燃烧作为自己的研究方向。读博期间,Spalding经历了诸多风波:最初安排的导师退休之后,学校给他安排了一个其他方向的导师,所以Spalding整个博士期间只能依靠自我激励。
不过大神终究是大神,1952年,Spalding顺利拿到了自己的博士学位,而他的博士课题也成为了他研究CFD的起点,他在论文中结合Von Karman的流体力学概念、Kruzhilin的传热概念以及Eckert的传质概念形成了他“统一理论”的雏形。
Spalding的CFD时代
博士毕业后,Spalding在剑桥待了两年,继续自己的科研工作。1954年,应Owen Saunders教授的邀请,Spalding来到了帝国理工学院,成为应用热力学的副教授。四年后,Spalding被任命为传热学的首席教授,随后当之无愧的成为计算流体力学的负责人。
虽然35岁的Spalding在当时已经展示出了自己的才华,不过当时的人们可能无法想象,在接下来三十多年的时光里,Spalding会在帝国理工学院创建影响全球的CFD团队。Spalding在帝国理工学院工作一直待到1988年退休为止,在最顶峰的1970年代,Spalding的团队拥有超过30位的科研人员,其中很多人都在后来成为CFD行业的大佬。

即便在今天,当我们回首Spalding和他的团队取得的学术成就的时候,都不得不感慨Spalding的学术嗅觉何等的敏锐,他在60多年前为整个科研团队的研究方向定下了基调:将CFD应用于工业领域,实现CFD的工程化。从学术到工程,最大的变化或许就是“别太较真,好用就行”。
而为了实现真正的工程化,简化和假设则不可避免,Spalding大胆的认为工程上大部分的流动都可以处理成定常不可压缩流动。而Spalding和他的团队更进一步的为现代CFD搭建了三块最重要的基石,也就是我们今天耳熟能详的:离散格式、数值方法以及湍流模型。
无离散不成CFD
我们知道,描述流体运动的N-S方程是典型的微分方程,而微分方程是无法被计算机直接识别并求解的,必须先转换为代数方程,并通过求解代数方程来获取原微分方程的近似解。将微分方程转换为代数方程,并基于离散好的网格进行数值求解,这一革命性的思想使得N-S方程在工程上的数值求解成为了可能。

在研究初期,Spalding和他的团队专注于“抛物型”流动(即抛物型偏微分方程所描述的流动),它有一个主要的流动方向。因此,方程可以通过从上游到下游的“行进”来求解,使用有限差分法可以应对该类型的问题。然而,Spalding发现大多数工业流动并不是单纯的“抛物型”问题,由于流动存在回流,流场中包含 “椭圆型”流动区域,即任意一点的扰动都会影响全场。因此,在Spalding的指导下,他的两名学生 Micha Wolfshtein 和 Akshai Runchal 开始致力于为这种“椭圆型”流动开发一种新的离散格式。而Runchal也在公开发表的文章《Brian Spalding: CFD & Reality A Personal Recollection》中回忆过这段往事。

Wolfshtein 和 Runchal最初采用标准中心差分格式的有限差分法求解。然而,他们很快发现,当雷诺数达到一定值的时候,矩阵系数会由正转负,导致高雷诺数下使用该方法无法收敛。Spalding敏锐的意识到,在一个对流占主导的流动中,使用中心差分是不合适的,因为上游对于流动的影响要远远大于下游,因此建议使用迎风格式代替中心差分。Spalding还举了一个有趣的例子——北面吹来的风总是很冷。
Spalding还提出了控制体的概念,启发Wolfshtein 和 Runchal开始思考使用通量而不是状态变量来进行数值计算,这也形成了我们今天熟知的“有限体积法”。而两人使用迎风格式代替中心差分的结果表明,迎风格式的本质使得它可以在任何雷诺数下收敛。
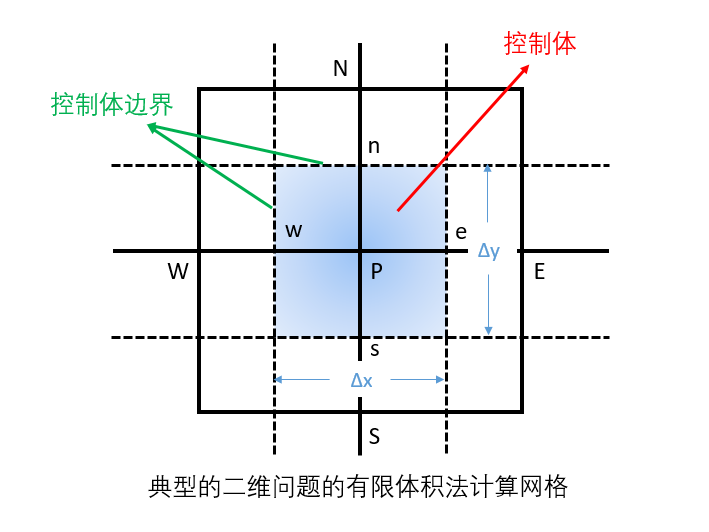
随后,Spalding进一步计算了一维对流和扩散问题的精确解,并认为中心差分对于小流量是合理的,但是随着流量的增加,上游的权重显著增加,需要改用迎风差分。因此,他提出了一种混合格式,即根据流场中对流与扩散的比例,在中心差分和迎风格式之间进行切换,该格式计算效率高,稳定性好,因此在CFD行业得到了非常广泛的应用。而Spalding和他的弟 子为离散格式所奠定的基础通过公开发表的论文和书籍传播到了全世界,并在CFD行业发扬光大。
不简单的SIMPLE方法
1969年,Spalding的团队将研究领域从二维流动扩展到三维。对于三维流动的边界层,其主流方向上具有“抛物型”行为,而其横流方向呈现二维“椭圆型”流动,因此需要该平面上的细微压力变化以确定横流速度。
在处理速度和压力分量时,人们发现对于棋盘式的分布(某网格节点两侧相邻节点的速度或压力相同),如果应用中心差分,则会发现它仍满足连续方程或动量方程,并在计算中会一直保持这种分布状态——但这显然是不真实的。虽然迎风格式不会出现这样的问题,但在许多情况下中心差分格式也不可或缺。为了一劳永逸的解决这个问题,Spalding提出了“交错网格”,即速度分量和压力存储在不同的网格系统上。
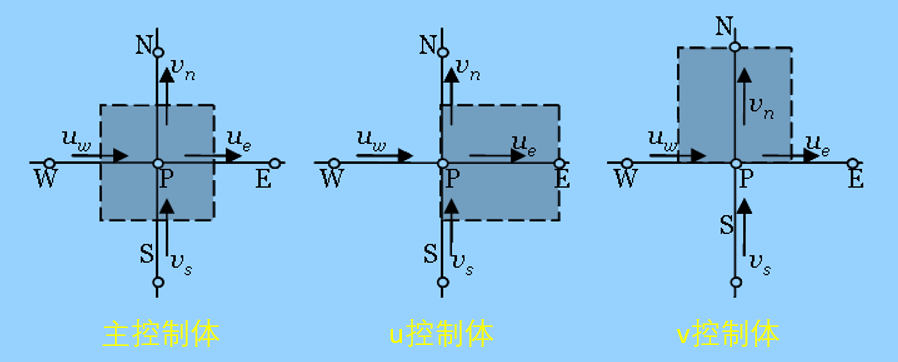
而为了求解横流平面中的 “椭圆型”流动,Spalding最初提出了同步变量调整的计算流程,即在控制体积上同时计算两个速度分量和压力以满足连续性方程和两个动量方程,然后通过逐点计算迭代得到整场的解。然而,这种方法需要的网格量很大,且收敛速度很慢,因此需要更合理的数值方法。这个时候,我们的广义师父Patankar该上线了。
1971年,已经博士毕业并回到印度的Patankar再次回到帝国理工学院,继续跟随自己的恩师Spalding从事CFD的研究。随后,在交错网格的基础上,两人共同提出了著名的SIMPLE算法。作为每一个CFDer都耳熟能详的的数值方法,SIMPLE算法最早由Patankar和Spalding在论文《A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows》中提出。SIMPLE方法的全名为压力耦合方程组的半隐式方法(Semi-Implicit Method for Pressure-Linked Equations),是目前工程上应用最为广泛的一种流场计算方法。

作为一种压力修正法,SIMPLE算法通过“先猜想后修正”的方法得到压力场,并求解离散化的动量方程。其基本思路如下:
基于给定的压力场,求解离散形式的动量方程,得出速度场。因为压力场是假定的或不精确的,这样,由此得到的速度场一般不满足连续方程,因此,必须对给定的压力场加以修正。修正的原则是:与修正后的压力场相对应的速度场能满足这一迭代层次上的连续方程。据此原则,把由动量方程和离散形式所规定的压力与速度的关系代入连续方程的离散形式,从而得到压力修正方程,由压力修正方程得出压力修正值。接着,根据修正后的压力场,求得新的速度场。然后检查速度场是否收敛。若不收敛,用修正后的压力值作为给定的压力场,开始下一层次的计算。如此反复,直到获得收敛的解。
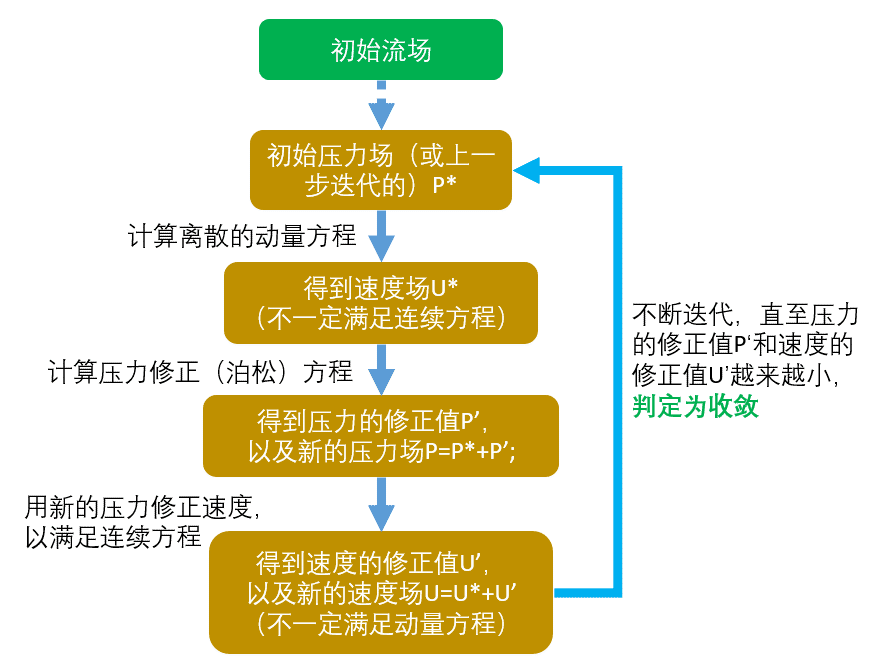
可以看到SIMPLE方法巧妙的解决了N-S方程中的一个大问题:速度分量同时出现在动量方程和连续方程中,导致各方程错综复杂的耦合在一起。而更复杂的压力项,仅出现在动量方程中,却没有可用于直接求解压力的方程。SIMPLE方法最重要的贡献便是实现了方程中速度和压力的解耦。而SIMPLE算法也成为了工程上应用最广泛的流场计算方法。
湍流计算的王牌
就在1964年,Patankar进入Spalding门下攻读博士的同年,年仅25岁的MIT博士Brian Launder回到帝国理工学院担任讲师,并加入Spalding的团队,开始了自己成为CFD大佬的成长之路。正如我们前面所说的,Spalding一直致力于CFD的工程化,其中很重要的一个研究方向就是为工业领域的流体仿真应用搭建合适的湍流模型,而Spalding将这一重要的研究方向交给Launder来领导。
Launder和他的博士生们从上个世纪60年代后期到70年代开展了大量的工作。1972年,Launder和他的博士生WP Jones在论文《The prediction of laminarization with a two-equation model of turbulence》中提出了k-epsilon模型,随后,他们又进行了一系列的测试,来校对湍流模型中的常数,最终在1974年Launder和Spalding共同署名的论文《The Numerical Computation of turbulent flows》中定义了我们今天所说的标准k-epsilon模型,该文章自问世以来已经超过两万次的引用。

在普朗特 “混合长度理论”的基础上,Launder融入了柯尔莫果洛夫的湍流理论,以一种更加湍流的思想,创造性的使用湍动能k和湍流耗散率epsilon来表示湍流粘性系数,而面对多出来的两个未知量,则通过补充两个微分方程来让RANS方程的求解封闭。关于k-epsilon模型的前世今生,前面的文章《始于实验,陷于仿真,忠于流体》已有非常完整的介绍,此处不再重复,感兴趣的朋友可以向前翻阅。
终生CFD
为了更好的实现CFD工业应用和高校研发之间的迭代,Spalding在1969年创办了一家公司。不过开始的时候,Spalding的公司主要承接的是政府和工业客户的定制化项目。直到1978年,Spalding和他的团队才着手创建世界上首个通用计算流体动力学软件并于1981年正式发布。
1988年, Spalding从帝国理工学院退休,一方面在自己的公司中继续从事CFD商业化的工作,另一方面,仍然没有停下自己CFD理论研究的脚步,每年至少会发表一篇高质量的论文。而作为英国皇家学会和皇家工程院的院士,Spalding在CFD方面的重大贡献也得到了全世界的认可,获誉无数。
时至今日,我们随便翻开一本计算流体力学的书或者打开一款CFD软件,里面的很多内容都直接或者间接的来源于Spalding和他的团队。Spalding将自己的一生都贡献给了CFD的研究和发展,直到2016年11月逝世,Spalding的一生和他的成就大概就是现代CFD的半部发展史。






