圣杯问题V:全纯微分(下)——完结篇
顾险峰(纽约州立大学石溪分校计算机系终身教授)


图10. 亏格为3的曲面上的叶状结构。
全纯二次微分的水平轨迹构成了曲面的一个叶状结构(Foliation),同样的,其铅直轨迹也构成了曲面的另一个叶状结构。所谓叶状结构就是将曲面分解为曲线的并集,每一条曲线被称为是一片叶子。每片叶子没有自相交,任意两片叶子没有交点。局部上看,相差一个微分同胚,叶子们彼此平行。每片叶子有可能是有限的圆,也有可能是无限的螺旋线。如果一个叶状结构的所有叶子都是有限圆,则这一叶状结构被称为是有限的。
大致而言,曲面 上两个叶状结构
上两个叶状结构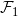 和
和 彼此等价,如果存在曲面的自微分同胚
彼此等价,如果存在曲面的自微分同胚 ,同胚映射将
,同胚映射将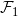 映到
映到 。那么曲面上任给一个叶状结构
。那么曲面上任给一个叶状结构 ,则存在一个全纯二次微分
,则存在一个全纯二次微分 ,
, 的水平轨迹和
的水平轨迹和 等价。有限叶状结构对应的全纯二次微分被称为是Strebel Differential。我们知道,所有的全纯二次微分构成线性空间,根据黎曼-罗赫定理,此空间实维数为6g-6,这里g是曲面的亏格。由此,如果我们掌握了全纯二次微分的计算方法,理论上我们就可以构成所有的叶状结构。圣杯问题的关键就在于寻求特殊的叶状结构。
等价。有限叶状结构对应的全纯二次微分被称为是Strebel Differential。我们知道,所有的全纯二次微分构成线性空间,根据黎曼-罗赫定理,此空间实维数为6g-6,这里g是曲面的亏格。由此,如果我们掌握了全纯二次微分的计算方法,理论上我们就可以构成所有的叶状结构。圣杯问题的关键就在于寻求特殊的叶状结构。
整体来看,曲面上给定一族不相交的简单闭曲线,这些曲线将曲面进行“裤子分解”,使得每个连通分支是带3个边界的拓扑球面,则存在一个Strebel Differential  ,过零点的水平轨线将曲面分解成拓扑环带,每个环带的基本群都是由一条给定的闭曲线生成。
,过零点的水平轨线将曲面分解成拓扑环带,每个环带的基本群都是由一条给定的闭曲线生成。 诱导的度量为每个拓扑环带配上了平直度量,后继的四边形网格化变得简单直接。同时
诱导的度量为每个拓扑环带配上了平直度量,后继的四边形网格化变得简单直接。同时 的零点结构非常标准,当表面四边形网格向内拓展成六面体网格时,体内的奇异曲线的条数最少,结构最为简单。这为体样条的生成带来了极大的便利。
的零点结构非常标准,当表面四边形网格向内拓展成六面体网格时,体内的奇异曲线的条数最少,结构最为简单。这为体样条的生成带来了极大的便利。
当晚,丘先生在麻省理工附近的五月花餐馆宴请大家,龙虾石斑,牛蛙刀蚬,异常丰盛,足见丘先生的欣慰之情。席间,丘先生郑重叮嘱老顾团队:“全纯二次微分对于共形结构的模空间至关重要;下一步,我们应该探索高阶全纯微分的计算方法,以及射影结构的模空间。”
一句话再度令老顾血脉贲张,为未来十年指明了努力方向。虽然目前没有人能够看出射影结构模空间的实际应用前景,但是老顾相信历史会再度重演。只要我们能够算出大自然内在几何结构的一部分,那么迟早人类的技术能够追赶上来,使得这一结构在实际领域中发挥根本的作用!
一年来的奔波劳顿,使得心灵又磨出一层老茧。感恩节降临,终于有时间和灵魂独处,内心也变得些许柔软。回顾十数年来的求索历程,宛若一名孤独的朝圣者,跋涉在优胜美地,虽然历尽艰辛,但是领略了大自然的雄奇壮丽。从数百年前黎曼开创的黎曼面理论,到阿尔福斯创立的拟共形几何理论,再到泰西米勒发展的泰西米勒空间理论,直至Strebel的全纯微分理论,一路走来,领悟了历史上许多大师的深邃哲思,既到达过人迹罕至的原始山林,也直面过峥嵘万仞的绝壁。为了将这些精美绝伦的抽象数学转化为平易近人的算法程序,只是追随前人数学家的足迹是远远不够的,绝大多数的时候需要辗转腾挪,独辟蹊径。生活的常态就是经年累月的殚精竭虑,冥思苦想。在抵御外在物质世界诱惑的同时,更为困难的是抵抗自身犹疑畏惧,轻言放弃的心魔。这种精神上的苦修,如人饮水,冷暖自知。当看到一个个以前只能用思想触及的几何结构,渐渐可以用计算机程序来把握,一个个数学定理渐渐融入计算机科学,那种精神上的满足,无法用语言来形容。
这条朝圣之路非常艰辛,这种苦修的学术之路和当代社会盛行的价值观念背道而驰。首先这需要纯粹数学和计算机科学两方面的知识结构,理论证明和工程实现两种不同的技巧,因此需要更长时间的学习和磨炼,而这是以青春为代价。其次,目前在学术标准日益被商业准则同化的氛围下,理论的深刻性和严格性让位于含混唯像的实用性。在过去,我们花了两年提出了高效的算法,却花了五六年来证明这一算法的严格性,这在当今工程领域被视为是保守迂腐的做派。特别是目前青年学者的生存压力空前巨大,在浮躁高压体制下花费五六年来完善一套理论无异于学术自 杀。很难想象会有年轻人为了美学价值而置身家性命于不顾,为了科学的纯洁崇高而主动殉道。对于青年学生而言,研习抽象深刻的几何理论无异于学习屠龙之术,青春耗尽而市场并无需求。相反的,有人只学习了表象的算法,虽然知其然却不知其所以然,却可以迅速创业,融资千万。更有很多学者学生,苦心孤诣,不懈求索,但却不被人理解。尤其是朋友家人用世俗的观念来衡量他们付出的心血,埋怨责骂,嘲笑讥讽。在强大的世俗压力下面,他们承受着难以想象的折磨和愤懑。这一切,每天都在老顾身边的朋友中发生。
在过去的一年中,依然有许多学者学生认同老顾的理念,主动和老顾合作,与老顾一同不改初衷,苦苦求索。更有很多长辈师长,对于老顾的研究工作大力支持,无私帮助。对于这些志同道合的师长和朋友,老顾诚挚地感激他们的学术支持,更由衷地敬佩他们的人格力量。对于那些依然在苦苦支撑的青年学者学生,老顾相信他们艰苦卓绝后终成大器。沧海横流,方显英雄本色!
[1] Xianfeng Gu and Shing-Tung Yau. Global Conformal Surface Parameterization. First
Eurographics Symposium on Geometry Processing (SGP03), Pages:127-137, Aachen, Germany, June 23-25, 2003.
[2] Na Lei, Xiaopeng Zheng, Jian Jiang, Yu-Yao Lin and Xianfeng Gu, Quadrilateral and Hexahedral Mesh Generation Based on Surface Foliation Theory, Computer Methods
in Applied Mechanics and Engineering, In Press, 2016.
[3] Kehua Su, Wei Chen, Na Lei, Junwei Zhang, Kun Qian and Xianfeng Gu, Volume Preserving Mesh Parameterization based on Optimal Mass Transportation, Journal of Computer-Aided Design (CAD), 2016.
[4] Xianfeng Gu, Feng Luo, Jian Sun and Tanqi Wu, A Discrete Uniformization Theorem
for Polyhedral Surfaces, Journal of Differential Geometry, Accepted 2016.
[5] Xianfeng Gu, Feng Luo, Jian Sun and Shing-Tung Yau, Variational Principles forMinkowski Type Problems, Discrete Optimal Transport, and Discrete Monge-Ampere
Equations, Vol. 20, No. 2, pp. 383-398, Asian Journal of Mathematics (AJM), April 2016.
[6]Lok Ming Lui, Xianfeng Gu, Shing-Tung Yau: Convergence of an iterative algorithm for Teichmuler maps via harmonic energy optimization. Math. Comput. 84(296), 2823-2842, (2015)
原文发于【老顾谈几何】,作者授权【WELSIM】转载




