[力学]从张量应变和工程应变开始谈起
[备注: 这篇讨论基于小变形假设]
在弹性力学教材中, 应变(strain)可以从两个角度介绍: 张量应变以及工程应变. 两者区别在于剪切应变的度量. 从概念上讲, 工程剪应变是两个微元线段夹角变化的度量, 而张量剪应变则是夹角变化的一半. 如果位移为 , 那么工程剪应变定义为
, 那么工程剪应变定义为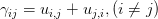 ; 与之相对于的张量剪应变则定义为
; 与之相对于的张量剪应变则定义为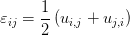
然而, 问题在于, 当我们把工程应变写成矩阵形式
的时候, 我们可以从数学上证明这个矩阵并不是一个张量. 相反, 张量应变(正如其名)则是一个张量.
那么, 对于一个有序数列, 需要满足什么条件才是一阶张量(也就是向量); 而对于一个方阵, 又需要满足什么条件才是二阶张量? 举个例子, 在3维空间里面, 点的位移 就是一个向量; 而一个椭球在
就是一个向量; 而一个椭球在 平面上的投影面积
平面上的投影面积 就并不是一个向量. 工程应变矩阵不是张量, 张量应变矩阵则是一个张量. 关键就在于一个一阶(或者二阶)有序数组在坐标变换下是否是旋转矩阵的一次(或者二次)齐次式. 譬如, 之前提到的投影面积在坐标变换的情况下, 面积是无法简单的通过变换法则计算的. 详细的可以看北京大学出版社"弹性力学教程".
就并不是一个向量. 工程应变矩阵不是张量, 张量应变矩阵则是一个张量. 关键就在于一个一阶(或者二阶)有序数组在坐标变换下是否是旋转矩阵的一次(或者二次)齐次式. 譬如, 之前提到的投影面积在坐标变换的情况下, 面积是无法简单的通过变换法则计算的. 详细的可以看北京大学出版社"弹性力学教程".
因此, 从数学的角度说, 工程应变有些奇怪. 然而, 我们还是经常使用工程应变, 下面说说其中一个原因.
我们从应变能密度 开始说. 应力可以从应变能对张量应变的偏导求得, 也就是
开始说. 应力可以从应变能对张量应变的偏导求得, 也就是 ,我们知道模量的定义来自于, 因此,
,我们知道模量的定义来自于, 因此,  . 而通过这个表达式, 我们可以发现
. 而通过这个表达式, 我们可以发现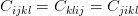 . 那么, 我们就可以得出
. 那么, 我们就可以得出
 , 根据对称性, 我们就可以得到
, 根据对称性, 我们就可以得到
. 因此, 在Voigt notation下, 很容易就写成
这个表达式看上去很漂亮, 但之所以所有的
 前的系数为1, 是因为我们做了这样的一个简化过程:
前的系数为1, 是因为我们做了这样的一个简化过程:  (其他下标类似). 然而, 当我们想要表达柔度矩阵的时候, 就会出现很有意思的事情. 注意柔度模量的定义
(其他下标类似). 然而, 当我们想要表达柔度矩阵的时候, 就会出现很有意思的事情. 注意柔度模量的定义
 , 在Voigt notation下, 我们有
, 在Voigt notation下, 我们有
因此, 我们要注意一点, Voigt notation下的柔度矩阵可以通过对Voigt notation求逆得到. 然而, 这个求逆所得的柔度矩阵的分量, 并不是柔度张量里面的分量, 而是有一些系数关系. 从本质上来说, 就是要认清Voigt notation是一种将四阶张量双点乘二阶张量的过程写成了一个矩阵点乘列向量的过程.
就简单说些, 不恰当的地方请指正.







