也是“猜”出来的狄拉克方程
为什么说“也”,因为前面已经存在一篇文章——《“猜”出来的薛定谔方程》,在该文最后提到,薛定谔方程是非相对论化的,适用于速度不太大的粒子,而由薛定谔方程改变后的狄拉克方程可以适用于高速运动的微观粒子。
同样,让我们先来看看狄拉克方程长什么样:

比起薛定谔方程,是不是感觉复杂了不少,其实这还不算,我需要告诉你的是:方程中的四个α不是常数,而是四个矩阵,每个α都是一个4×4的矩阵(行数×列数),因此,相应地,作为方程的解,波函数Ψ是一个4×1的矩阵,换而言之,狄拉克方程是一个方程组,有四个解。
面对这么复杂的一个方程,狄拉克是如何“猜”出来的呢?让我们依然从狭义相对论开始说起。
根据狭义相对论[1]:

当 -1<x<1 时,可以将以下函数f(x)展开成麦克劳林级数(即关于 x 的幂级数)[2]:
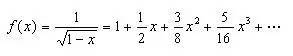
对比上下两式,将E的表达式写成麦克劳林级数形式:

从而可以得到能量展开式:

从以上这个式子,我们可以知道,在经典力学中,由于速度v非常之低,v和光速c相比可以忽略不计,因此上式中从第三项开始就略去不计,但在其能量表达式中,通常也不包含式中的首项(该项也称为静止能量项),因此,能量E记为(p为动量):

读者也许会问,那为什么在这种非相对论能量表达式中,不需要包含静止能量项呢?原因在于:静止能量这一项没有包含速度v,而在经典力学里,我们只讨论质点的能量如何依据速度而变化的问题;当一个物系中发生的能量变化ΔE大到足以使所引起的质量(严格来说是惯性质量)变化达到可以观察的程度时,才考虑在能量表达式中加入静止能量项,比如在核反应的情况下就是如此[3]。
对于高速运动的自由微观粒子,相对论能量的近似表达式一般记为:
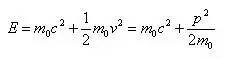
同时给出其相对论能量的精确表达式[4]:

在近似表达式中,为什么一般情况下仅仅保留能量展开式中前两项?当速度v等于十分之一光速c、甚至四分之一光速c时,读者可以自行计算一下第三项和第二项的比值。
假如该高速运动粒子又在一个势场V之中,则该粒子的能量关系式为:
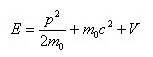
因此,p通过E表示如下:

阅读仔细的读者看到这个式子,估计脑海中会闪过一个念头:根据《“猜”出来的薛定谔方程》一文中的内容,将上式代入到波函数Ψ对x、t的导函数式子,如此就可以求得相对论化的一维和三维薛定谔方程了:
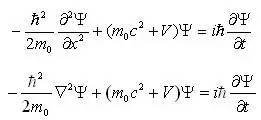
这样的式子正确么?从建立的过程看,形式上没错,但没有考虑方程两边的偏导阶数平衡。原因在于:狭义相对论中,时间t和空间坐标(x,y,z)的地位是等同的,t、x、y、z共同构成了四维时空坐标,而在上面两式中,波函数Ψ对(x,y,z)是二阶偏导,但对t是一阶偏导,这就导致了对同等时空坐标(x,y,z,t)偏导的不平衡;因此,求解相对论化的薛定谔方程,波函数Ψ对(x,y,z,t)的偏导必须同阶,都是一阶、或都是二阶;但是波函数Ψ对t进行二阶及以上偏导时,会导致波函数Ψ的概率统计失去意义[5],比如克莱因-戈登方程就是把波函数Ψ对t作二阶偏导,使得最后的计算结果出现了负概率。
正是基于以上的考虑,狄拉克选择用波函数Ψ对四维时空坐标(x,y,z,t)统一作一阶偏导,以此作为其工作的起点。在正式讲述狄拉克是怎么“猜”方程之前,还需要一些知识准备:量子力学中的能量算符和动量算符。
我们先来回顾一下《“猜”出来的薛定谔方程》一文中提到的波函数Ψ的解析式:

我们用波函数Ψ求出对 t、x 的一阶偏导:

整理以上两式,可得(此式中动量只有x方向):

由此引出能量算符和动量算符:
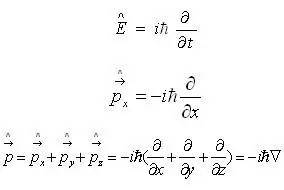
能量E与波函数Ψ相乘,等于能量算符作用于波函数Ψ;同样,动量p与波函数Ψ相乘,等于动量算符作用于波函数Ψ。不过这样的运算对应规则只适用于直角坐标系下,如要过渡到其他坐标系,可以先在直角坐标系中使用这些算符,然后再做坐标变换以过渡到其他坐标系[6]。
举个例子简要介绍一下能量算符和动量算符怎么用(动量只考虑x方向):

上式两边同乘以波函数Ψ,根据算符运算法则[7],将得到:

上面得到的最后一式正是非相对论化的自由粒子的一维薛定谔方程。
谈了这么久,终于要谈到狄拉克了,因为假使没有之前的知识积累,将看不懂狄拉克方程的建立过程。
在没有外加势场V的情形下,高速自由粒子的能量精确表达式为:

上式两边同乘以波函数Ψ,得到:

这种带有根号的二阶偏导方程,处理起来相当困难,这势必需要换一种思路。
狄拉克设想:如果让能量E和动量p的关系呈线性,那么使用能量算符和动量算符就可以使得波函数Ψ对四维时空(x,y,z,t)的一阶偏导达到统一,从而,能量动量关系与相对论的时空变换得以自洽,而这需要对能量动量关系进行因式分解[8]。
这样一种设想作为“猜测”方程的起始引导显得极其重要,因为很有可能会决定了以后的工作是失败还是成功;接下去的几个“猜测”步骤也十分关键。正是这个开始的设想以及之后的几个步骤,将狄拉克的数学物理天赋体现得淋漓尽致。
狄拉克先将能量表达式中的矢量进行标量化处理:

式子中,根号下面是四个分量平方之和,狄拉克假定(以后的事实表明,他这样的假定是正确的)能量E和四个分量之间存在着最简单的一次线性关系,于是,可以拼凑出一个去掉根号的待定系数方程[9]:

前后式子对比一下,而后平方,我们可以得到:

上式的右边展开以后,再和左边比较,可得:
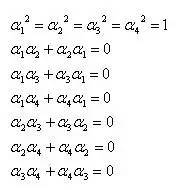
这个方程组在实数范围内、复数范围内都没有解!从后面六个方程形式来看,可以发现,任意两个α之间的乘积位置不具备互换性,而是具有方向性,因此狄拉克想到了用矩阵来解决问题。以后我们将上述的七个方程称为狄拉克矩阵。
狄拉克首先想到的就是当时已经存在的泡利矩阵(一组2×2的矩阵,关于泡利矩阵是怎么来的,这是另外一个话题),因为泡利矩阵的运算结果和狄拉克矩阵非常相似,我们先来看泡利矩阵的具体内容:

与狄拉克矩阵很相似是不是?有了这么好的基础,接下来的工作就容易多了—— 一组2×2的矩阵描述了三个泡利矩阵,而狄拉克矩阵有四个;再通过观察泡利矩阵中各元素的分布规律和取值特点,而后分析出狄拉克矩阵的特征值、矩阵对角线元素的正负对称性、矩阵阶数的奇偶性;于是,狄拉克猜测自己所要的矩阵应该为4×4矩阵[10]。基于泡利矩阵,经过组合与拼凑,狄拉克给出了一组解:

狄拉克矩阵的这组解被称为“泡利组”,需要说明的是,这不是狄拉克矩阵的唯一解,比如,物理学家费米也给出了一组解,一般把这组解称为“标准组”:

现在我们已经把狄拉克矩阵的解求出,这意味着相对论化的能量动量线性关系式也就确定了,式中的四个待定系数是四个4×4的矩阵,这四个矩阵构成一个矩阵组,并且这四个矩阵相互之间满足狄拉克矩阵的运算结果,用数学表示:

现在把上面的能量动量线性关系式两边同乘以波函数Ψ,再根据能量算符和动量算符,我们就可以得到自由粒子的狄拉克方程,注意方程中的偏导阶数,波函数Ψ对四维坐标(x,y,z,t)统一做了一阶偏导:
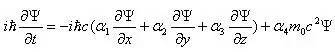
当然这个式子还可以作简化,我们设定:

那么之前的自由粒子的狄拉克方程可以简写成:
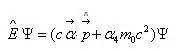
假若粒子还处于一个势场V之中,则此时的狄拉克方程为:

当然也可以写成具有直观物理意义的狄拉克方程,也就是文章一开始就写出的那个巨复杂的方程:

由于狄拉克方程中的系数是4×4矩阵,所以方程的解,波函数Ψ就是一个4×1矩阵,即,狄拉克方程的解是四个波函数Ψ:

这不像薛定谔方程那样只有一个解,也正是因为这4个波函数Ψ,狄拉克最后求解出电子具有负能态,从而预言存在电子的反粒子——反电子(也由此引发了“狄拉克之海”一说),之后被实验确认,从此让世人知道了反物质。
狄拉克方程还有一个最简写法:
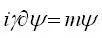
不得不承认,这个方程的确非常简洁,但是,也非常不易理解,如果要从一般的狄拉克方程推导至该式,还需要引进四维时空算符和一些量子场论的符号。
关于狄拉克方程,值得一提的还有,这个最简方程被刻在了狄拉克的墓碑上,而这块墓碑就置放于伦敦威斯敏斯特教堂内(俗称西敏寺),那里长眠着很多伟大的人物。

参考资料:
[1]《大学物理学-力学》,清华大学出版社,1999年
[2]《高等数学-下册》,高等教育出版社,1996年
[3]《狭义与广义相对论浅说》,爱因斯坦-著,杨润殷-译,北京大学出版社,2006年
[4] 同[1]
[5]《量子迷宫》,巴戈特-著,潘士先-译,科学出版社,2012年
[6]《量子力学》,苏汝铿-著,高等教育出版社,2002年
[7] 同[6]
[8]《一念非凡:科学巨擘是怎样炼成的》,曹则贤-著,外语教学与研究出版社,2016年
[9]《克莱因-戈登方程和狄拉克方程》(论文),黄鹏辉,2010年
[10] 同[6]
作者简介:
董广宇,新浪ID:@闻道_wendao,货币金融研究者,倡导建立一套诚实健康自由购买力稳定的货币系统,从业于商业银行,著有《被忽视的货币真相》一书,经营有“少数派财经报告”公 众号。




