光（二）

牛顿的粒子物理论是这么的成功， 难怪当初解释光行为时，他也按照粒子论方法处理。 无论如何， 观察到的光是走直线的，且光从镜面反射时如一个球碰在一个硬墙上一样。牛顿制造了第一台反射式望远镜， 解释了白光是由彩虹光合成的， 在光学中作了那么多工作， 可他总是基于光是由一种称为微粒的小粒子流组成的假说。 光线在穿过光疏质和光密质边界时， 正如光从空气到水或玻璃中变弯（ 这就是为何搅酒棍在酒杯或桶中看来是弯的），只要假设微粒在光密质中走得快一点就能解释光折射现象。 即使在牛顿时代， 仍有与之完全不同的解释。荷兰物理学家克里斯汀 惠更斯生于 1629年 ， 虽 比 牛 顿 大13岁 ， 也 算 是同时代的人他得出一个观点光并是粒子流，而是一种波。 就像水波在海面或湖面上传播一样， 光通过一种不可见的“ 透明的以太” 传播。 就像在湖塘里扔一颗石子引起的波传播 那样，光在以太中传播是从光源出发到各个方向的波理论在解释反射和折射时能同粒子说一样合理。 虽然说在光密质的物质中的光波速度加快， 在当时的十七世纪没有办法测量光速， 因此这方面的差别不足以区分这两种理论的优劣。可是，有一个关键的方面， 在这点上可得到可以观测到的不同预测。 当光通过一个尖锐的边界时，它形成一个明显的边界影子。这极像粒子流的行为， 因为它沿直线运动。 而波动要转弯或散射， 以某种方式绕进暗影里（ 想象一下， 水塘中的涟漪是能够绕过石头的） 。 三百年前，这种现象很明显对粒子论有利， 而波动理论虽未被忘记却也给抛弃了。然而到了十九 世纪 ， 两种 观点 的状况则完全反过来了。

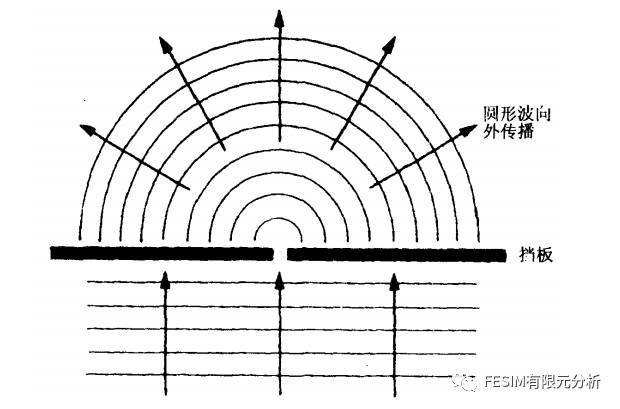
水波的衍射

在十八世纪， 很少人能认真地看待光的波动说。 在这极少数人中，当时数学的带头人，曾对几何，微积分和三角几何做出主要贡献的瑞士数学家雷纳德*欧拉不仅认真地对待光的波动说，而且还写文章支持这种学说。 说起欧拉，现代数学与物理全由算术项和方程描述， 数学描述所依赖的技巧大部分是由欧拉创立的。在此过程中，他创立了至今仍被使用的符号缩写，如表示的开方根（ 我们还会与表示圆周率； 一起遇到它） ； 被数学工作者使用的积分运算符号 。很 奇怪 的是，在《大英百科全书》 的欧拉条目中没有提到他的波动观点。

——《寻找薛定谔的猫》