清华笔记:计算共形几何讲义 (13)Koebe 迭代收敛性
顾险峰 纽约州立大学石溪分校
计算机与应用数学系 终身教授
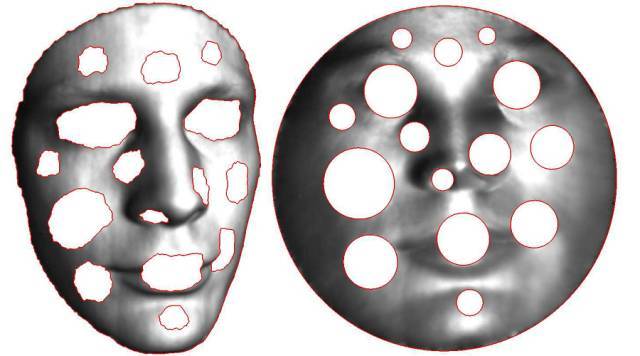
图1. 亏格为0、带有多个边界的曲面到平面圆域(Circle Domain)的共形映射。
这节课我们讲解亏格为零、带有多个边界曲面的共形模(conformal module)。如图1所示,带有多个洞的人脸曲面可以保角的映射到带有圆洞的平面圆盘(circle domain)上。这种映射彼此相差一个莫比乌斯变换。




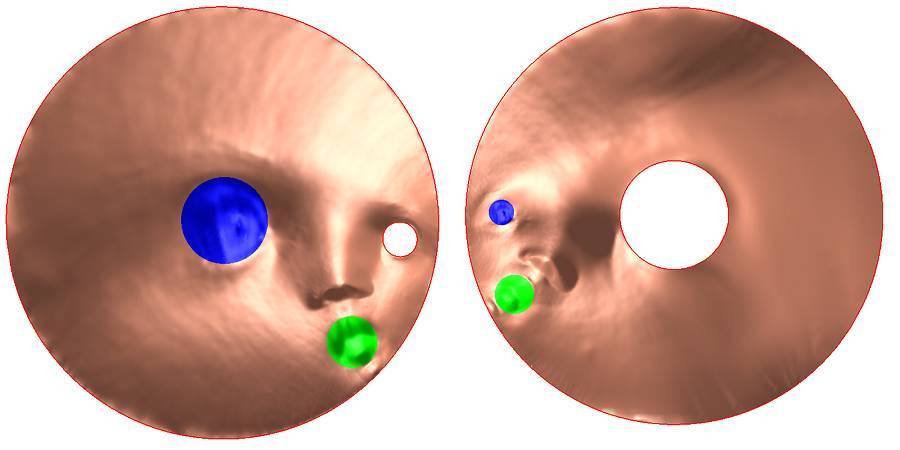
图2. Koebe迭代。
如图2所示,多联通区域到圆域(circle domain)的共形映射可以用Koebe迭代方法计算。假设多联通区域为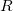 ,其边界为
,其边界为
 ,
,
这里 为外边界,其他
为外边界,其他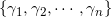 为内边界。在第
为内边界。在第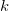 步骤,我们将所有内边界填充,只留下
步骤,我们将所有内边界填充,只留下 ,这里指标
,这里指标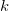 代表模
代表模 再加上1,得到
再加上1,得到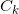 ,然后计算共形映射:
,然后计算共形映射: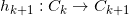 ,这里
,这里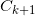 是标准环带,
是标准环带,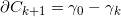 ,
, 为标准同心圆。在第
为标准同心圆。在第 步骤,我们将
步骤,我们将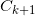 的内圆
的内圆 填充,将
填充,将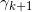 打开,然后计算
打开,然后计算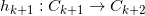 ,将
,将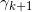 映成内圆。这时,原来的内圆
映成内圆。这时,原来的内圆 不再是标准圆形。如此反复,所有内边界形状越来越接近圆形;以至无穷,所有内边界都收敛成标准圆形。
不再是标准圆形。如此反复,所有内边界形状越来越接近圆形;以至无穷,所有内边界都收敛成标准圆形。
Koebe迭代算法优美和谐,目前为止难以被其它方法所取代。但是其收敛性的证明深奥而繁难,角标系统相对复杂。
给定圆周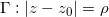 ,关于圆周反射定义为
,关于圆周反射定义为
 。
。
我没说两个平面区域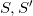 关于圆周
关于圆周 对称,如果
对称,如果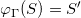 。如果
。如果 不是圆周,区域
不是圆周,区域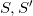 和曲线
和曲线 同时包含在一个平面区域
同时包含在一个平面区域 中,和定义在
中,和定义在 上的共形映射
上的共形映射 ,使得
,使得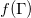 成为标准圆周,
成为标准圆周,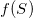 和
和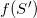 关于
关于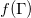 对称,这时我们依然说
对称,这时我们依然说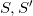 关于曲线
关于曲线 对称,并记成
对称,并记成
 。
。
假设全纯函数 定义在上半平面上,同时 F 在实数轴上取值为实数,那么函数可以被延拓成定义在整个复平面上,
定义在上半平面上,同时 F 在实数轴上取值为实数,那么函数可以被延拓成定义在整个复平面上,
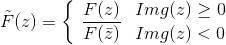 。
。
因为上半平面和单位圆盘共形等价,因此如果全纯函数 F 定义在单位圆内部,并且单位圆的取值在单位圆上,那么应用Schwartz 反射, F 可以被延拓到单位圆外部。

图3. 共形变换诱导的形变。
引理:假设A是一个拓扑环带,具有共形模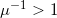 ,内、外边界分别为Jordan曲线
,内、外边界分别为Jordan曲线 ,那么
,那么
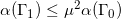
并且
 ,
,
这里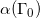 是曲线
是曲线 所围绕的面积。
所围绕的面积。
证明:令全纯函数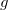 将标准环带
将标准环带 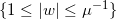 映到拓扑环带A,
映到拓扑环带A,

那么,
 ,
,
 ,
,
因此,我们得到
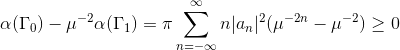 。
。
直径 被更大集 合
被更大集 合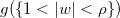 的直径所界定,这里
的直径所界定,这里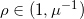 。这些集 合的直径被边界
。这些集 合的直径被边界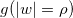 长度的一半所界定。于是我们有
长度的一半所界定。于是我们有

由Schwartz引理,我们得到

等价的
 ,
,
两边对 进行积分,即得第二个公式。证明完毕。
进行积分,即得第二个公式。证明完毕。

图4. Koebe's 迭代图解。
我们令 ,包含无穷远点,
,包含无穷远点,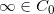 ,其在复平面上的补集为
,其在复平面上的补集为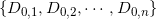 ,其边界为
,其边界为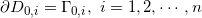 。
。
存在双全纯函数,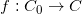 ,将多联通区域
,将多联通区域 映到圆域
映到圆域 。圆域
。圆域 的补集为标准圆盘
的补集为标准圆盘 。同时在无穷远点附件,全纯函数具有归一化的形式,
。同时在无穷远点附件,全纯函数具有归一化的形式,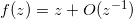 。
。
应用黎曼映照,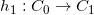 ,将区域
,将区域 映成单位圆
映成单位圆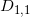 ,同时
,同时 ,
,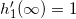 。这样
。这样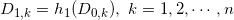 。如此反复,在第
。如此反复,在第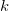 步, 构造黎曼映照
步, 构造黎曼映照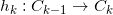 ,将
,将 映成单位圆
映成单位圆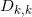 ;
; 在
在 点归一化,
点归一化,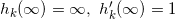 。我们规定记号如下:
。我们规定记号如下:

构造双全纯映射:
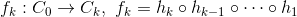 ,
,
和从圆域 到
到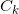 的双全纯映射,
的双全纯映射,
 ,
,
在无穷远点归一化,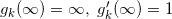 。
。
因为 是标准单位圆,
是标准单位圆,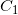 能够关于
能够关于 进行反射,其镜像记为
进行反射,其镜像记为 。黎曼映照
。黎曼映照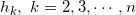 定义在
定义在 上,区域
上,区域

满足
 。
。
映射 在
在 上没有定义,但是它将边界
上没有定义,但是它将边界 映成标准圆,根据对称性原则,
映成标准圆,根据对称性原则, 可以被延拓,延拓后的
可以被延拓,延拓后的 将
将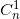 映成
映成 ,并且
,并且
 。
。
重复迭代过程,我们得到一个序列 ,满足对称关系:
,满足对称关系:
 。
。
同样, 是标准圆,
是标准圆, 是
是 关于
关于 的对称像,
的对称像,
 ,
,
这里,每个 映射都需要用反射原则(reflection principle)来解析延拓。我们有对称关系:
映射都需要用反射原则(reflection principle)来解析延拓。我们有对称关系:
 。
。
同样,对于任意的 ,
,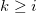 ,我们定义区域
,我们定义区域 ,使得对称关系成立:
,使得对称关系成立:
 。
。
经过第一轮迭代,所有的区域 都被定义。因为
都被定义。因为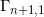 再度成为单位圆,我们定义
再度成为单位圆,我们定义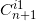 为
为 关于
关于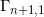 的反射图像。
的反射图像。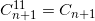 ,但是其他的
,但是其他的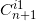 为新生成的区域。应用延拓后的黎曼映照,我们得到一系列的镜像区域:
为新生成的区域。应用延拓后的黎曼映照,我们得到一系列的镜像区域:
 ,
,
同样,我们可以定义镜像区域:
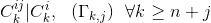 ,
,
经过 轮迭代,我们得到
轮迭代,我们得到 重镜像
重镜像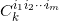 ,满足对称关系:
,满足对称关系:
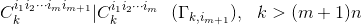 。
。

图5. 圆域上的多重镜像反射。
考察映射 ,我们有
,我们有
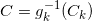
不依赖于角标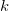 。同样,所有
。同样,所有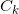 的多重镜像
的多重镜像
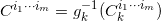 ,
,
及其边界
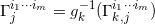 。
。
圆域 的n个边界
的n个边界 都是圆,彼此相离。这些边界曲线都是
都是圆,彼此相离。这些边界曲线都是 多重镜像,也都彼此相离。
多重镜像,也都彼此相离。
我们在w-平面上进行如下操作。我们将所有的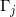 同心放大,直至有两个圆相切,这时的圆记为
同心放大,直至有两个圆相切,这时的圆记为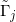 ,放大系数为
,放大系数为 。我们将
。我们将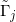 关于
关于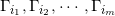 进行多重反射,其镜像记为
进行多重反射,其镜像记为
 。
。
令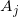 表示标准环带,其边界为
表示标准环带,其边界为
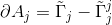 ,
,
其共形模为
 ,
,
它的任意镜像都具有相同的共形模
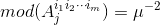 。
。
这些标准环带在共形映射下的像也具有相同的共形模 ,我们记为
,我们记为
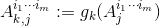 ,
,
其边界为
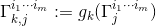 。
。
我们的目的是估计全纯函数  ,圆域的
,圆域的 重镜像反射是
重镜像反射是

每个圆盘的边界为
 ,
,
这里的指标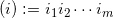 ,满足任意相邻的一对脚标不等,同时
,满足任意相邻的一对脚标不等,同时 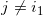 。我们选择一个足够大的圆周
。我们选择一个足够大的圆周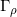 ,包括所有的初始补集圆盘
,包括所有的初始补集圆盘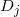 ,对于一切属于初始圆域的点
,对于一切属于初始圆域的点
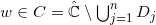 ,
,
根据柯西公式(Cauchy formula)
 ,
,
因为 , 当
, 当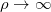 时
时
 ,
,
对于余下的积分,因为  在所有的圆
在所有的圆  之外,积分
之外,积分
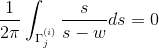 。
。
对于任意复数 ,积分
,积分
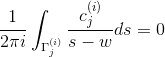 ,
,
我们得到
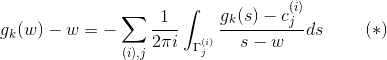
令距离常数
 ,
,
我们有 ,因为
,因为  ,
, 。更进一步,我们定义
。更进一步,我们定义
 ,
,
曲线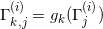 在半径为
在半径为 的圆中,我们将
的圆中,我们将 选成这个圆的圆心,那么对于一切
选成这个圆的圆心,那么对于一切 ,
,
 ,
,
积分路径的长度是 ,这里
,这里 ,由(*)式我们得到
,由(*)式我们得到
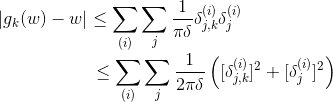
由引理,考虑以 为边界的拓扑环带,我们得到估计
为边界的拓扑环带,我们得到估计
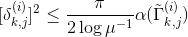
同时,
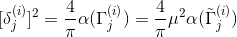 。
。
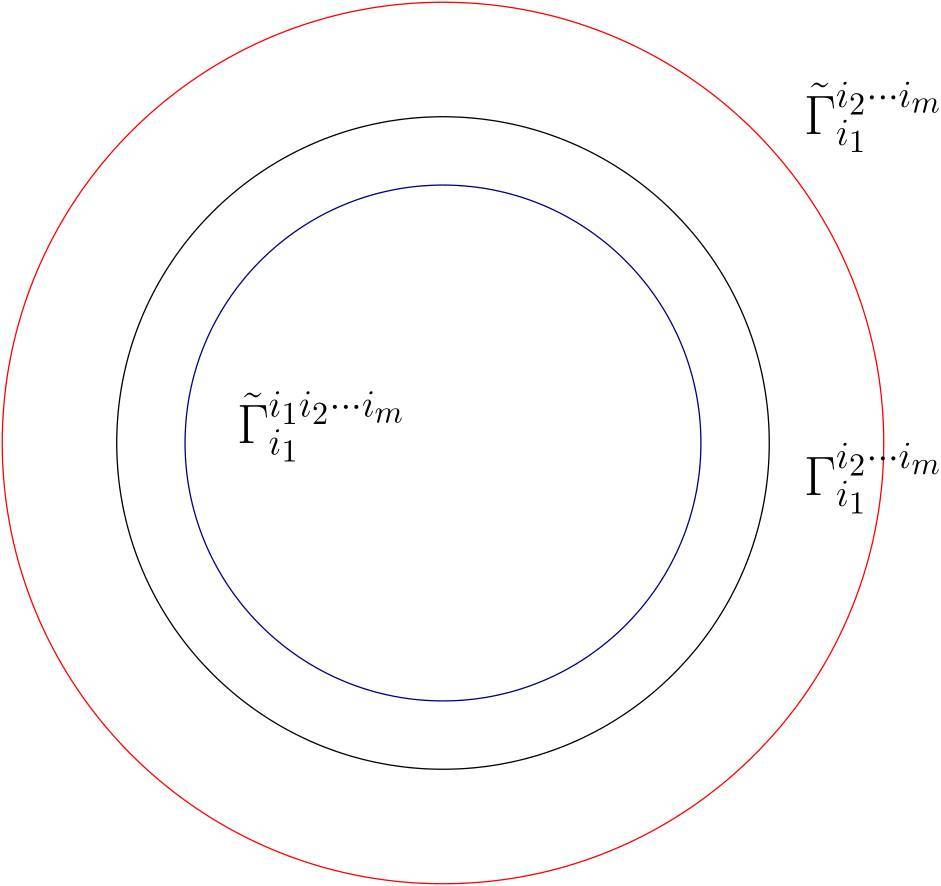
图6. 标号图解。
考察所有的圆 ,它们都在圆盘
,它们都在圆盘 的内部,因为
的内部,因为

因此所有这些圆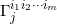 都在
都在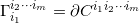 之内,因此也都在
之内,因此也都在 之内。我们得到不等式:
之内。我们得到不等式:
 ,
,
同样的
 ,
,
考察环带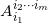 ,其边界为
,其边界为
 ,
,
共形模为
 。
。
同理,考察 的像,
的像,
 。
。
所有圆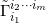 都包含在
都包含在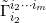 内,因此
内,因此

继续下去,我们得到
 ,
,
最后一项求和式的值等于所有圆盘 的面积和乘以
的面积和乘以 ,我们记之为
,我们记之为 。至此,我们得到
。至此,我们得到
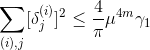 。
。
同样的,在z平面上,我们得到估计
 ,
,
这里 是所有曲线
是所有曲线 所围区域的面积之和。
所围区域的面积之和。
如果所有的标准圆盘 都包含在大圆
都包含在大圆 之内。全纯函数
之内。全纯函数  在区域
在区域 上是单值的(univalent),根据Koebe 1/4定理,圆域
上是单值的(univalent),根据Koebe 1/4定理,圆域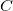 的像
的像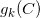 包含
包含 ,由此我们得到估计
,由此我们得到估计
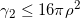 。
。
综上所诉,我们得到最终的估计,当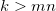 时:
时:
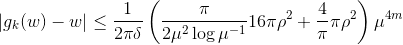
至此,我们证明了Koebe迭代算法的收敛性,给出了收敛阶。




