论文学习|第七篇(2)基于传感器融合的钛合金薄壁件铣削多工况识别(铣削实验以及结果讨论)
非常尊重并感谢科研人员做出的辛勤贡献!若有侵权,烦请联系处理!
若有翻译不当之处,恳请批评指正!
本篇研究论文针对加工过程中颤振和刀具磨损的同时识别比较困难的问题,提出了一种基于传感器融合的多工况识别方法。从声音、加速度、切削弯矩信号中提取多传感器特征,并且筛选特定频段内的传感器数据特征,提出了改进的主成分分析方法。适合于颤振检测、特征融合、信号处理研究领域者学习。
本篇将介绍第2篇:铣削实验以及结果讨论
正文共: 7510字0图
预计阅读时间: 19分钟
论文信息
论文题目:Multi-condition identification in milling Ti-6Al-4V thin-walled parts based on sensor fusion
期刊、年份:Mechanical Systems and Signal Processing,2022
作者:Runqiong Wang(a), Qinghua Song(a,b,*), Zhanqiang Liu(a,b), Haifeng Ma(a,b), Zhaojun Liu(c)
机构:(a) Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Ministry of Education, School of Mechanical Engineering, Shandong University, Jinan, PR China
(b) National Demonstration Center for Experimental Mechanical Engineering Education, Shandong University, Jinan, PR China
(c) School of Information Science and Engineering, Shandong University, Jinan, PR China
目录
1. 引言
2. 提出的多工况识别方法
3. 铣削实验
4. 结果
5. 讨论
6. 结论
摘要
Ⅲ 铣削实验
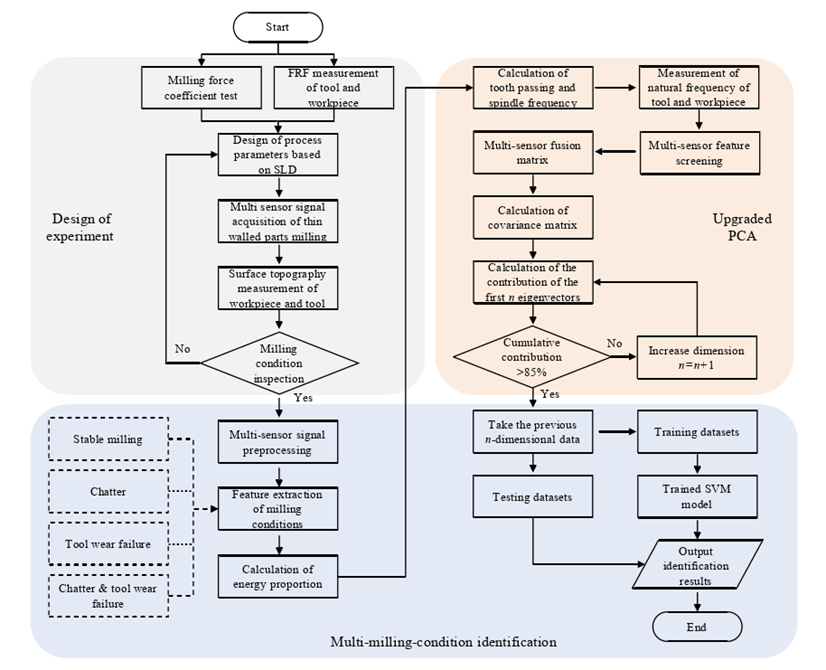
如图2所示,在三轴立式数控机床(VMC0540D)上进行铣削实验,同时采集加工过程中沿y方向的铣削弯矩、工件加速度和声音信号。铣削弯矩信号由带传感器的刀柄采集,通过无线传输模块传输到PC记录系统。加速度传感器(Dytran 3145A1,灵敏度10.20
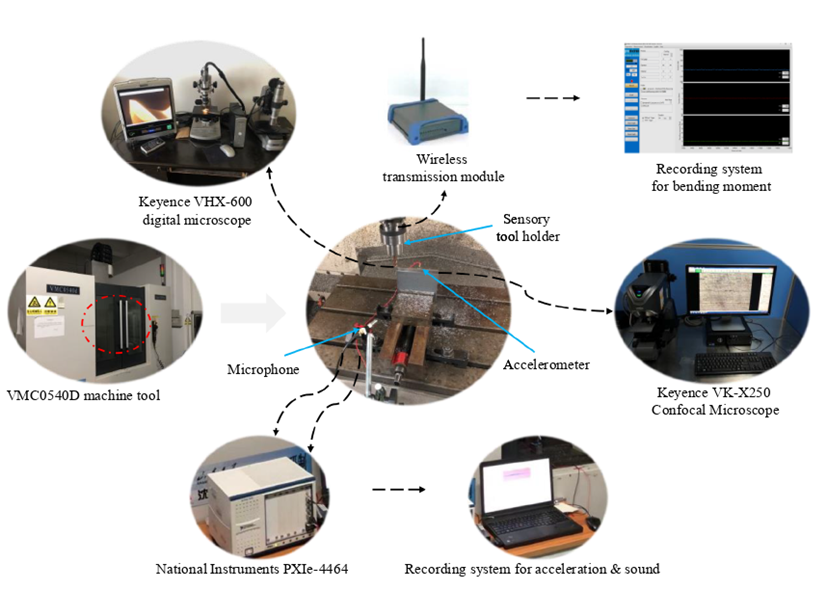
 图3 刀具和工件的频响函数
图3 刀具和工件的频响函数 


3.3 信号获取
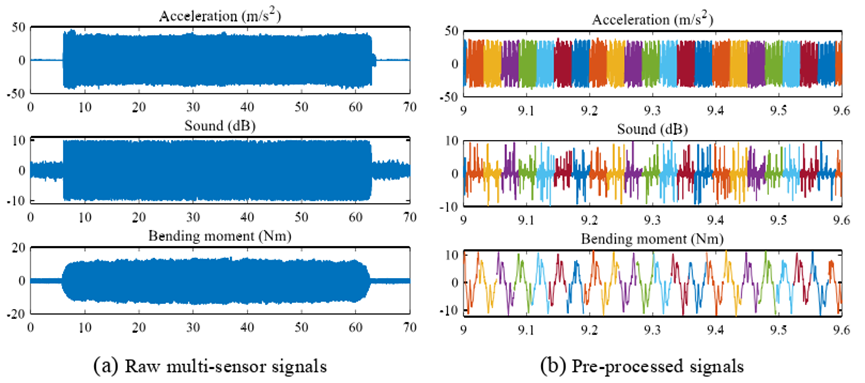
Ⅳ 结果




4.2 多工况识别
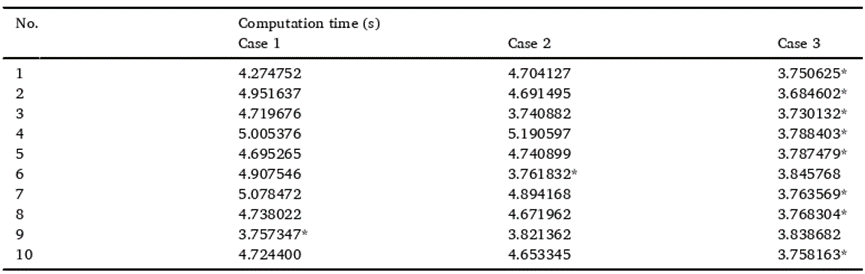
表3 训练分类器时的最优参数
表3可以看出,传统PCA方法处理的特征数据的最优交叉验证精度低于其他两种方法。这主要是因为传统的PCA方法在降维过程中不能过滤掉多传感器特征中的冗余信息,而是对数据集进行统一的变换,导致与识别结果相关的特征丢失。改进的PCA方法基于刀具和工件的固有频率、主轴旋转频率和过齿频率,根据降维前的先验知识筛选提取的特征,通过多传感器融合保持原始数据集结构。此外,从表3可以看出,方案 2和方案 3在训练数据集中的预测准确率是一致的,即特征矩阵是否包含能量占比并不影响分类准确率。这是因为两个参数的优化是在训练数据集中进行的,目的是在不知道测试集标签的情况下选择最优参数。然而,能量占比对识别结果的影响取决于测试数据集的分类精度,因此有必要进一步评估。

Ⅴ讨论


Ⅵ 结论
注明
1、本篇论文到此介绍完结。
2、若需引用本文的公式、专业术语等内容建议再细读原论文核实;若本文对您的论文idea有帮助,建议引用原论文~
参考文献
[1] Rw A , Qsa B , Zla B , et al. Multi-condition identification in milling Ti-6Al-4V thin-walled parts based on sensor fusion[J]. Mechanical Systems and Signal Processing, 164.




