用MATLAB对SAR ADC建模之新手指南
本文来源:模拟集成电路
SAR ADC简介
体重、血糖,体脂等等。这些模拟信号都得最终放在电脑,手机等数字领域进行处理,存储或者传输,那如何把模拟信号转换成数字信号呢?就需要一个转换器芯片,它就是芯片界的翘楚—ADC!

上图是不同类型ADC的转换速率-精度分布图。
用MATLAB建立简单的模型
简单模型如
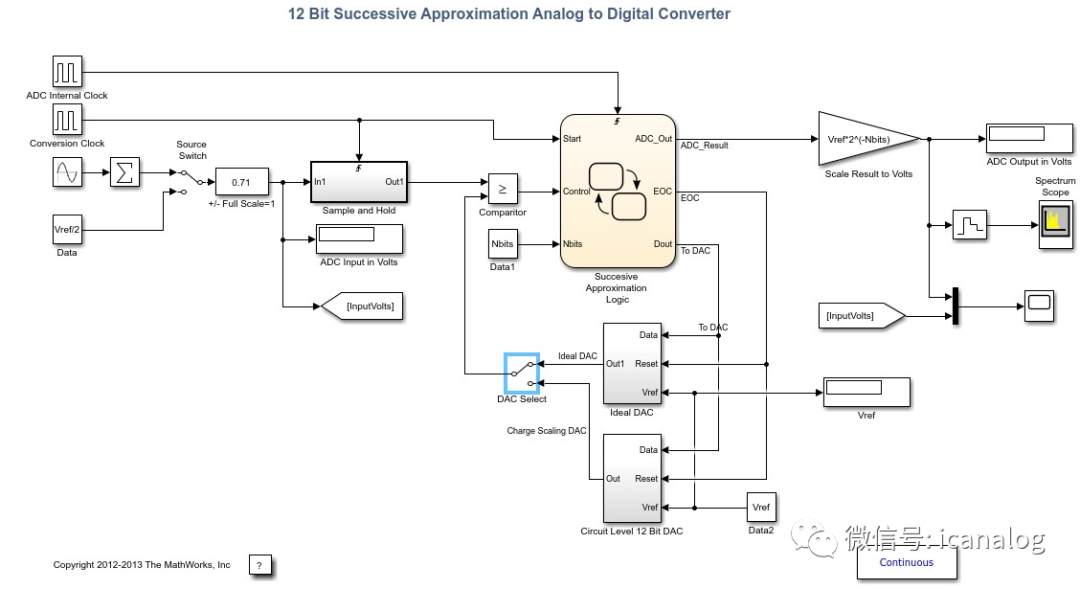
MATLAB基本操作
在MATLAB中主要用的模块是simulink,也可以使用代码编写,由于是入门本次使用更直观的模块仿真。
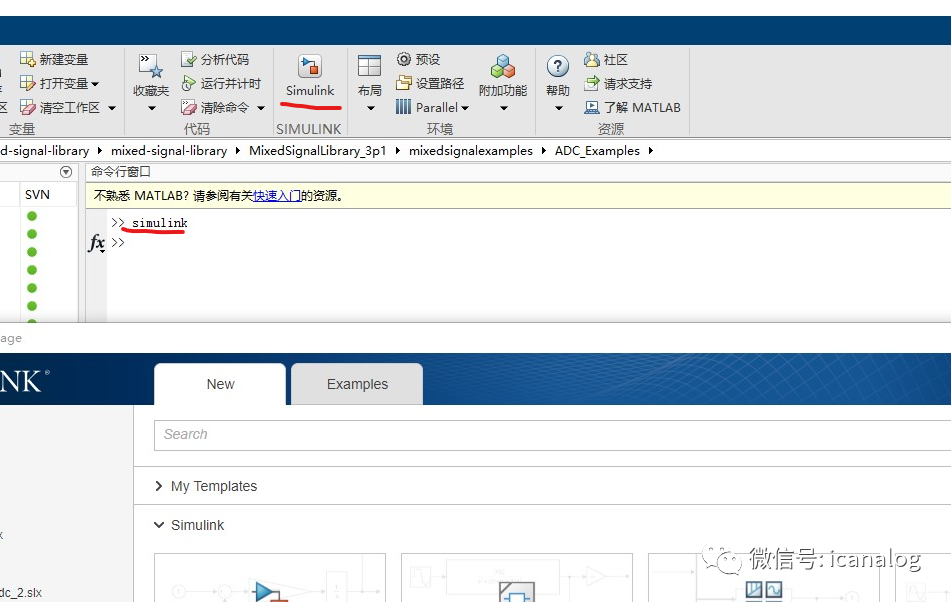
启动
simulink的启动非常的简单,既可以直接点击图像进行启动,也可以在函数输入地方输入simulink进行启动,如下图所示
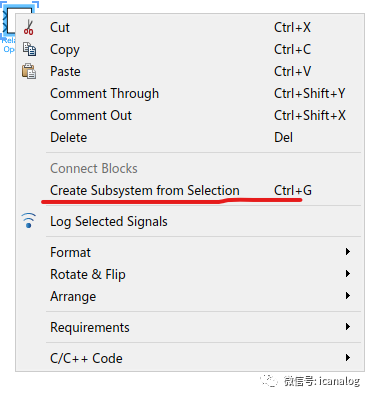
模块的封装
在做一个很大的电路的时候经常需要非常大的空间实现一个功能,这样看起来非常的复杂,需要将完成一个这样功能的所有电路封装成一个只有输入输出的模块。这样有利于进行逻辑的分析。完成这一功能只需要将需要封装的电路选中,然后右键create subsystem from selection 或者快捷键 ctrl +G
状态转移图
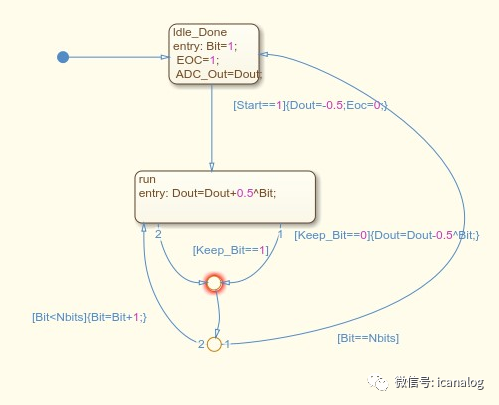
这是MATLAB中的state flow 在simulink中的new下方可看到 state chart就可以创建这个东西。
条件是有限状态系统中,条件必须定义在[]括号中。当一个时间发生时,只有当[]括号中的语句为真或非零时,带有条件标签的转移才有效。转移可以同时拥有事件和条件;条件要放在事件名之后。当转移标签既有事件又有条件时,只有当指定的事件发生并且条件为真时转移才有效。一个流程图中,以{}表示的动作仅仅是一个可执行的动作。
状态转移图可以对应数字电路中的时序转移图,所以这个state flow用于对数字逻辑的建模。
model exploer

在这个工具中用于查看和修改模块的一些参变量的值,也可以使用其他一些功能。
一些其他模块,上述已有图形不在重复
采样保持电路

ideal DAC
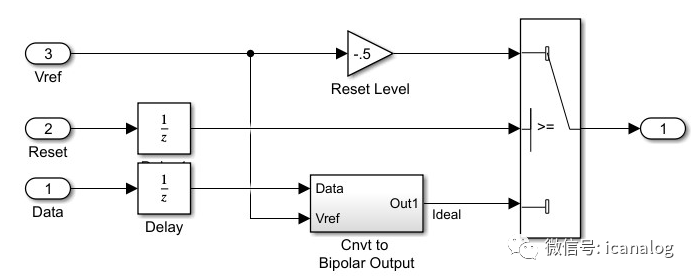
Circuit level 12bit DAC

仿真和显示

模型的基本工作原理
ADC的基本原理

图2-1 为一个典型ADC 的基本框图[26],包括抗混叠滤波器、采样保持电路、量化器和编码器四个部分。首先输入信号Vin 通过一个抗混叠滤波器,抗混叠滤波器是一个低通滤波器,其目的是用于避免高频信号在ADC的基带中造成混叠效应,通常抗混叠滤波器是利用ADC 本身的带宽有限特性来实现的。根据奈奎斯特(Nyquist)采样定理[26]:采样频率必须至少是原始信号带宽的2 倍,才能避免原始信号信息的丢失。因此,抗混叠滤波器的截止频率一般设置为采样频率的一半。输入信号经过抗混叠滤波之后进入一个采样保持电路,该电路采样模拟信号并将
其离散化,在保持阶段保持电压固定不变,以便后面量化器能正确量化。离散化的输入信号通过量化器进行量化,模数转换即是通过量化步骤来完成。对于一个精度为N 的ADC,参考电压被量化器分割成2N 个大小相同的子区间,量化步骤通过找到与输入电压相对应的子区间即完成了量化。编码器是将量化输出的数字位按照一定的规则进行编码,并最终得到与模拟输入电压对应的数字输出码,这样就完成了模拟信号到数字信号的转换过程。常用的编码方式有二进制码、非二进制码、2 的补码、温度计码和格雷码等。
SAR ADC 的基本原理

一般来说,差分电容ADC是由一组二进制权重的电容对组成的,从而提高位电容之间的匹配性,同时也能减小寄生电容效应带来的影响。对于采用电容式DAC结构的SAR A/D转换器,DAC本身也同时集成了采样保持的功能。比较器在时钟信号的控制下比较差分电容DAC的模拟输出,并将比较结果传递到SAR逻辑控制。SAR根据比较器输出依次得到数字码并将其锁存以便转换完成后进行统一输出,同时通过相应的逻辑产生控制信号,控制差分电容DAC完成逐次逼近的过程。
第一个比较周期,Vip大于Vin,所以D1=1,同时Vip和Vin分别向共摸电平平移1/4Vref;第二个周期,Vip仍旧大于Vin,所以D2=1,同时Vip和Vin分别向下向上平移1/8Vref;第三个周期,Vip小于Vin,所以D3=0,此时Vip向上平移1/16Vref,而Vin向下平移1/16Vref;这过程冲重复到整个转换完成。
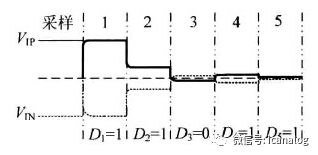
可以将模块的功能与MATLAB中的模型对应起来




