【知识】晶格的周期性与常用晶格
1
晶格的周期性
原胞和基矢晶格的共同特点是具有周期性,因此晶格周期性可以用原胞和基矢来描述。原胞是晶体中体积最小的周期性重复单元,当它平移布拉维格子所有可能的格矢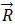 时,将精确地填满整个空间,没有遗漏,也没有重叠。
时,将精确地填满整个空间,没有遗漏,也没有重叠。
对某一晶格,尽管习惯上常取三个不共面的最短格矢为基矢,但原则上基矢的取法并不唯一,原胞亦有多种取法。但无论如何选取,原胞均有相同的体积,平均每个原胞只包含一个格点。在有限大的晶体中所含原胞数和格点数相等。人们常选用维格纳—塞茨原胞,简称WS原胞,以晶格中某一格点为中心,作与其近邻的格点连线的垂直平分面,以该点为中心所围成平面的最小体积属于该点的WS原胞。显然,属于某一格点的WS原胞由空间内最接近该点的区域所构成。图1给出了一个二维布拉维格子的WS原胞,它的构造中不涉及对基矢的任何特殊选择,所以它与相应的布拉维格子有完全相同的对称性,因此也将WS原胞称为对称化原胞。
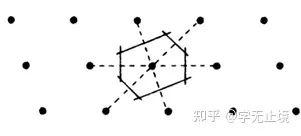
图1 二维布拉维格子的WS原胞
由于晶格的周期性,可以把基矢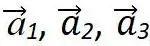 为三个棱边所组成的平行六面体作为晶格结构的重复单元,它们平行地堆积在一起,互相没有交叠,可以充满整个晶格。这样的结构重复单元称为单胞。由子格点处在平行六面体的顶角上,每一原胞共有八个顶角面每一顶角又为八个原胞所共有,故每个单胞只含有一个格点,它是体积最小的结构重复单元,其体积为:
为三个棱边所组成的平行六面体作为晶格结构的重复单元,它们平行地堆积在一起,互相没有交叠,可以充满整个晶格。这样的结构重复单元称为单胞。由子格点处在平行六面体的顶角上,每一原胞共有八个顶角面每一顶角又为八个原胞所共有,故每个单胞只含有一个格点,它是体积最小的结构重复单元,其体积为:
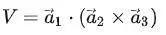
这恰好是平均每一格点所占的体积。除了周期性外,每种晶体还有自己特殊的对称性,为了同时反映晶格的对称性,往往选取体积较大的结构重复单元,称为晶胞。
2
简单立方晶格
原子球在一个平面内呈正方排列,如图2所示。这样的原子层叠加起来得到简单立方格子,用原点表示原子的位置,即得到其相应的晶格结构。

图2 简单立方格子
简单晶格中,某一个单胞只包含一个原子,所有的原子在几何位置和化学性质上是完全等价的。碱金属具有体心立方晶格结构;Au、Ag和Cu具有面心立方晶格结构,它们均为简单晶格,原胞中只包含一个原子。
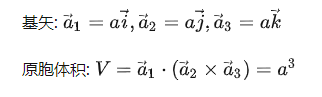
3
体心立方晶格
体心立方晶格结构如图3所示,体心立方原子球排列的方式可以表示为: AB AB AB……, 体心立方晶格中,A层中原子球的距离等于A-A层之间的距离,要做到这一点需A层原子球的间隙:△=0.31r0(r0 :原子球的半径)。具有体心立方晶格结构的金属: Li、Na、K、Rb、Cs、Fe等。

图3 体心立方格子
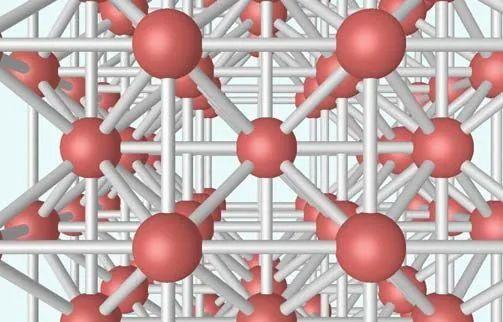
图4 体心立方格子晶胞
体心立方晶格的晶胞如图4所示,除顶角上有格点外,在立方体的中心处还有一格点,故称为体心立方。晶胞的边长为a ,称为晶格常数。将这种晶胞平行堆积起来就得到体心立方晶格,平均每个晶胞含有两个格点。每个晶胞的顶角都是相邻晶胞的心,所有格点都是等价的, 故体心立方晶格是一种布拉菲晶格,其单胞的基矢可以选为:
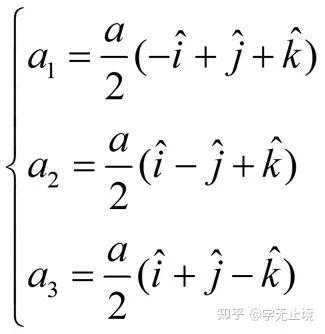
式中 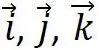 为直角坐标系的三个单位矢量。单胞的体积为
为直角坐标系的三个单位矢量。单胞的体积为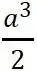 ,是晶胞体积的一半。
,是晶胞体积的一半。
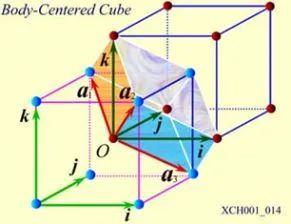
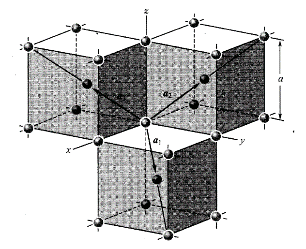
图5 带有直角坐标系的体心立方格子
4
六角密排晶格
原子在晶体中的平衡位置,排列应该采取尽可能的紧密方式,对应于结合能最低的位置。一个原子周围最近邻的原子数,可以被用来描写晶体中粒子排列的紧密程度,这个数称为配位数。晶体中最大配位数与可能配位数的数目不同。晶体由全同的一种粒子组成,将粒子看作小圆球,则这些全同的小圆球最紧密的堆积称为密堆积,密堆积所对应的配位数,就是晶体结构中最大的配位数。全同的小圆球平铺在平面上,任一个球都与6个球相切。每三个相切球的中心构成一个等边三角形,并且每个球的周围有6个空隙,这样构成的一层,计为A层,第二层也是同样的铺排,计为B层,第三层也是同样的铺排,计为C层。把B层的球放在A层相间的3个空隙里,第二层的每个球和第一层的三个球紧密相切,如图6所示。
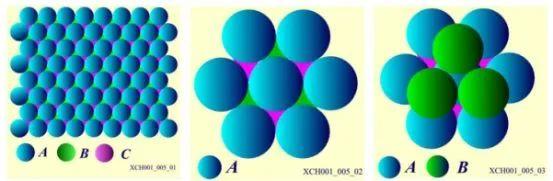
图6 密堆积排列
第三层C层有两种不同的堆法。C层原子排列之一:六角密排晶格。原子球排列方式为: AB AB AB……,如图7所示。在层的垂直方向是6对称性的轴,这个垂直方向的轴就是六角晶系中的c轴,Be、Mg、Zn、Cd具有六角密排晶格结构。
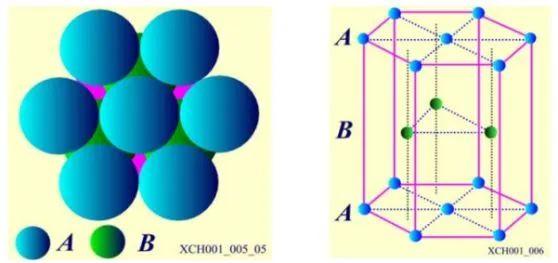
图7 六角密排晶格
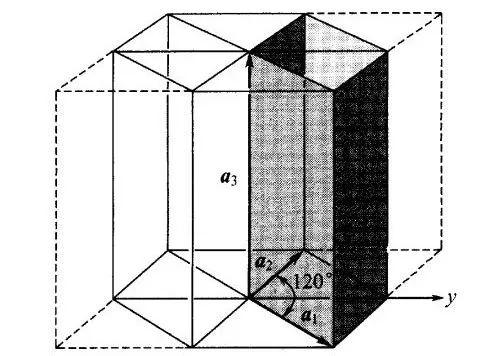
图8 六角晶系的原胞与六角对称棱柱的关系,其中 a1=a2≠a3 。
5
面心立方晶格
C层原子排列之二: 面心立方晶格,原子球排列方式为: ABC ABC ABC,如图9所示。层的垂直方向是对称性为3的轴,就是立方体的空间对角线。Cu、Ag、Au、AI具有面心立方晶格结构;
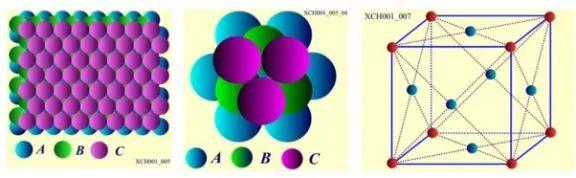
图9 面心立方晶格
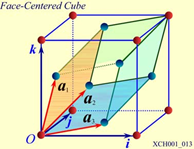
图10 面心立方晶格的晶胞
图10为面心立方晶格的晶胞。除顶角外,在立方体六个面的中心处还有一个格点,故称为面心立方。每个面为两个相邻的晶胞所共有,每个面心格点只有二分之一是属于一个晶胞,而处于顶角上的每个格点只有八分之一属于一个晶胞,所以每个面心立方晶胞只含有4个格点。把晶胞平行堆积起来不难看出,处于面心和顶角上的格点是等价的,每一格点周期的情况完全相同,面心立方晶格也是一种布拉菲晶格。其原胞的基矢可以选为:
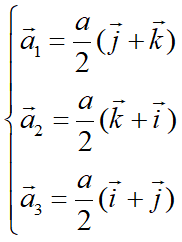
原胞的体积:
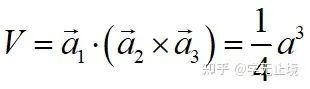
单胞基矢:
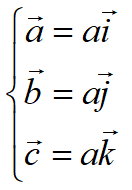
单胞的体积:
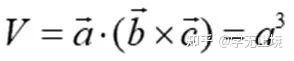
原胞的体积为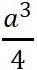 ,是单胞体积的四分之一 。因为原胞的选择不是唯一的,所以我们也可以选择对称性更高的原胞。例如。以每一格点为中心,作它与最近邻和次近邻格点联线的垂直平分面,这些面围成一个封闭的多面体,晶格将被这些多面体平行堆积所充满,每个多面体就是一个原胞,称为威格纳—赛兹原胞。图是二维布拉菲晶格的威格纳—赛兹原胞,每个维格纳赛兹原胞只含一个格点,每个格点都位于原胞的中心,它的对称性显然要比通常的平行六面体原胞高。面心立方晶格的威格纳赛兹原胞为十二面体,而体心立方晶格的威格纳赛兹原胞为截角八而体,即十四面体。
,是单胞体积的四分之一 。因为原胞的选择不是唯一的,所以我们也可以选择对称性更高的原胞。例如。以每一格点为中心,作它与最近邻和次近邻格点联线的垂直平分面,这些面围成一个封闭的多面体,晶格将被这些多面体平行堆积所充满,每个多面体就是一个原胞,称为威格纳—赛兹原胞。图是二维布拉菲晶格的威格纳—赛兹原胞,每个维格纳赛兹原胞只含一个格点,每个格点都位于原胞的中心,它的对称性显然要比通常的平行六面体原胞高。面心立方晶格的威格纳赛兹原胞为十二面体,而体心立方晶格的威格纳赛兹原胞为截角八而体,即十四面体。
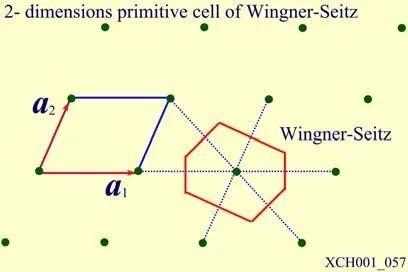
图11 维格纳赛兹原胞

图12 面心立方晶格的威格纳赛兹原胞
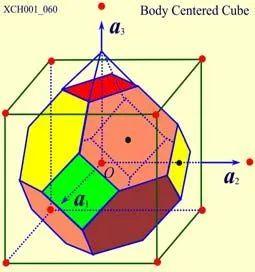
图13 体心立方晶格的威格纳赛兹原胞
综上所述,晶体结构的周期性是通过布拉菲晶格来体现的,只要把基元按同样规律安放在格点上就得到实际的晶体结构,每一个布拉菲格点和一个原胞相对应,原胞的平行堆积充满整个晶格,原胞中的任一点 与另一原胞的相应点
与另一原胞的相应点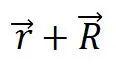 应有相同的物理性质,这就是晶格的平移对称性。显然,严格的平移对称性只能在无限大的晶体中才能实现,但实际晶体的尺寸通常比晶格周期大好几个数最级,故除了专门研究表面的性质外,可以近似地把晶体看成是无限大。
应有相同的物理性质,这就是晶格的平移对称性。显然,严格的平移对称性只能在无限大的晶体中才能实现,但实际晶体的尺寸通常比晶格周期大好几个数最级,故除了专门研究表面的性质外,可以近似地把晶体看成是无限大。
6
金刚石晶格结构
金刚石由碳原子构成,在一个面心立方原胞内还有四个原子,这四个原子分别位于四个空间对角线的四分之一处。一个碳原子和其它四个碳原子构成一个正四面体。如图14所示分别为金刚石和石墨晶格结构。重要的半导体材料如Ge、Si等,都有四个价电子,它们的晶体结构和金刚石的结构相同,如图15所示。
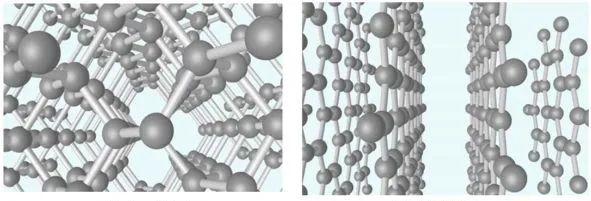
图14 金刚石(左)和石墨烯(右)结构
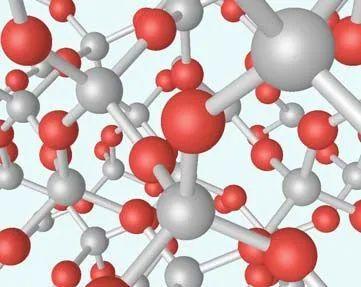
图15 硅晶体结构
7
几种化合物晶体的晶格
NaCI晶体的结构如图16所示。氯化钠由Na+ 和 Cl− 结合而成,是一种典型的离子晶体, Na+ 构成面心立方格子,Cl− 也构成面心立方格子。两个面心立方子晶格各自的原胞具有相同的基矢,只不过互相有位移差。
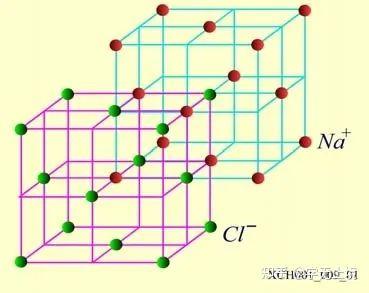
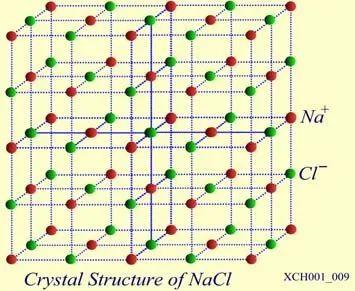
图16 NaCI晶体的结构
CsCl晶体的结构:CsCl是一种典型的离子晶体,其结晶学原胞如图17所示。CsCl结构是由两个简单立方的子晶格彼此沿立方体空间对角线位移二分之一的长度套构而成。
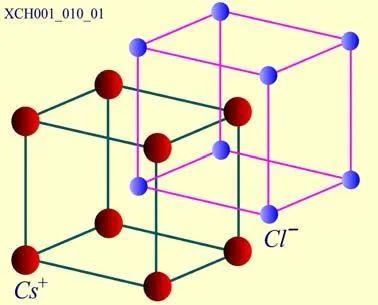
图17 CsCl晶体的结构
ZnS晶体的结构:立方系的硫化锌具有和金刚石类似的结构,其中硫和锌分别组成面心立方结构的子晶格,沿空间对角线位移四分之一的长度套构而成,这样的结构统称闪锌矿结构。如图18所示。许多重要的化合物半导体,如锑化铟(InSb)、砷化稼(GaAs)等都是闪锌矿结构,在集成光学上很重要的。

图18 ZnS晶体的结构
钙铁矿结构: 指钛酸钙 (CaTiO3) 的结构。许多重要的介电晶体,例如: 钛酸钡(BaTiO3)、锆酸铅(PbZrO3)、铌酸锂(LiNbO3)、钽酸锂(LiTaO3)等都属于此类型结构。
钛酸钡的晶胞如图19所示,在立方体的顶角上是钡(Ba),钛(Ti)位于体心,面心上是三组氧(O)。三组氧(OI,OII,OIII)周围的情况各不相同,整个晶格是由Ba、Ti和OI、OII、OIII各自组成的简单立方结构子晶格(共5个)套构而成的钙铁矿结构。
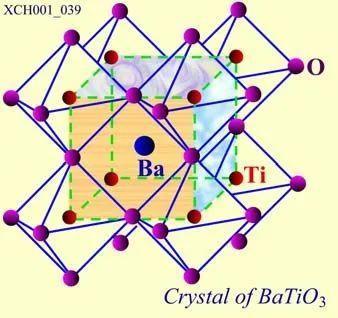
图19 钛酸钡的晶胞
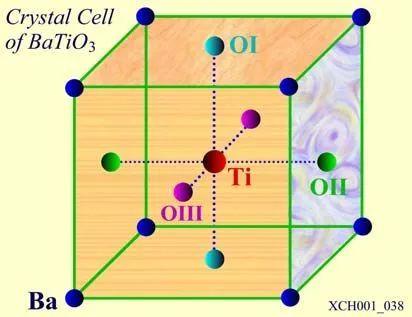
图20 Ti的氧八面体排列
如图20所示,如果把OI、OII、OIII连结起来,它们构成一个等边三角形,整个原胞共有8个这样的三角形面,围成一个八面体,整个结构可看作为氧八面体的排列,钡(Ba)在8个氧八面体的间隙里。钙铁矿型的化学式可写为ABO3,其中A一般代表一价或二价的金属,B代表四价或五价的金属,且常把BO3称为氧八面体基团。氧八面体是钙铁矿型晶体结构上的特点,它与这类晶体的一些重要物理性质有很大关系。实际上,许多具有亚铁磁性的晶体(通称铁氧体),也具有氧八面体结构,但不属钙铁矿型。氧八面体结构和金刚石或闪锌矿型中的正四面体结构是固体物理领域中非常受重视的两大典型结构。
//
名词解释:
·原胞: 一个晶格中最小重复单元(体积最小)。
·基矢: 原胞的边矢量,三维格子的重复单元是平行六面体,基矢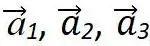 是重复单元的边长矢量。在一些情况下,单胞就是原胞,而在一些情况下,单胞不是原胞,例如面心立方晶格。
是重复单元的边长矢量。在一些情况下,单胞就是原胞,而在一些情况下,单胞不是原胞,例如面心立方晶格。
·单胞(结晶学元胞): 为了反映晶格的对称性,常取最小重复单元的几倍作为重复单元。单胞的边在晶轴方向,边长等于该方向上的一个周期,代表单胞三个边的矢量称为单胞的基矢。
往期推荐:

信息来源:知乎、电介质学术交流(JAD)
声明:本文所用图片、文字部分源于网络,目的为非商业性知识分享,版权仍属于原作者,如信息有误或涉及版权问题,请第一时间通知,我们将立即处理!




