材料参数的非线性拟合方法
在有限元计算中,我们经常需要处理一些离散数据的拟合问题,这里我们介绍一种通过Matlab进行任意非线性函数拟合的方法。
例如,在热弹塑性分析中,我们需要对一组通过试验测得的材料初始屈服应力随温度变化的离散数据进行拟合,相应的离散数据如下表所示。

表1 材料初始屈服应力随温度变化
在对材料参数进行拟合之前,我们首先根据表中给出的离散数据确定应该使用何种函数曲线进行拟合,即确定拟合的函数模型。
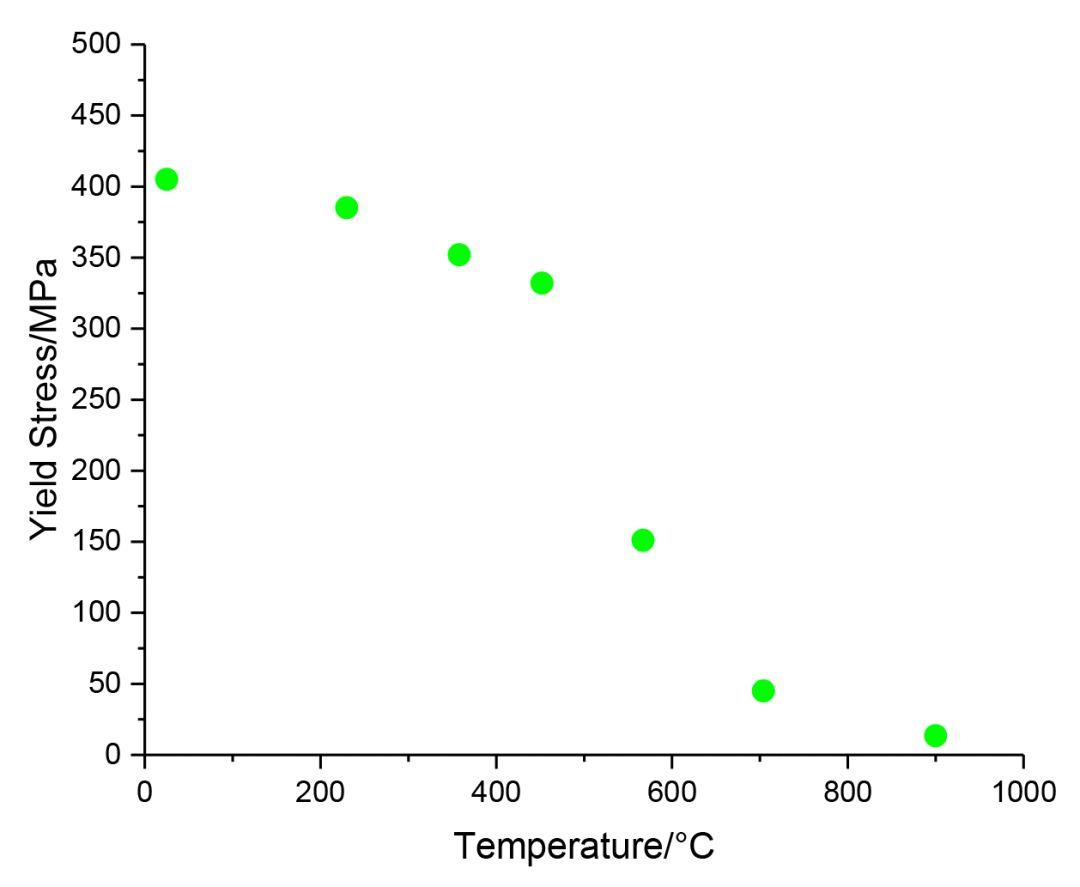
离散数据散点图
目前典型的函数模型有以下几种。
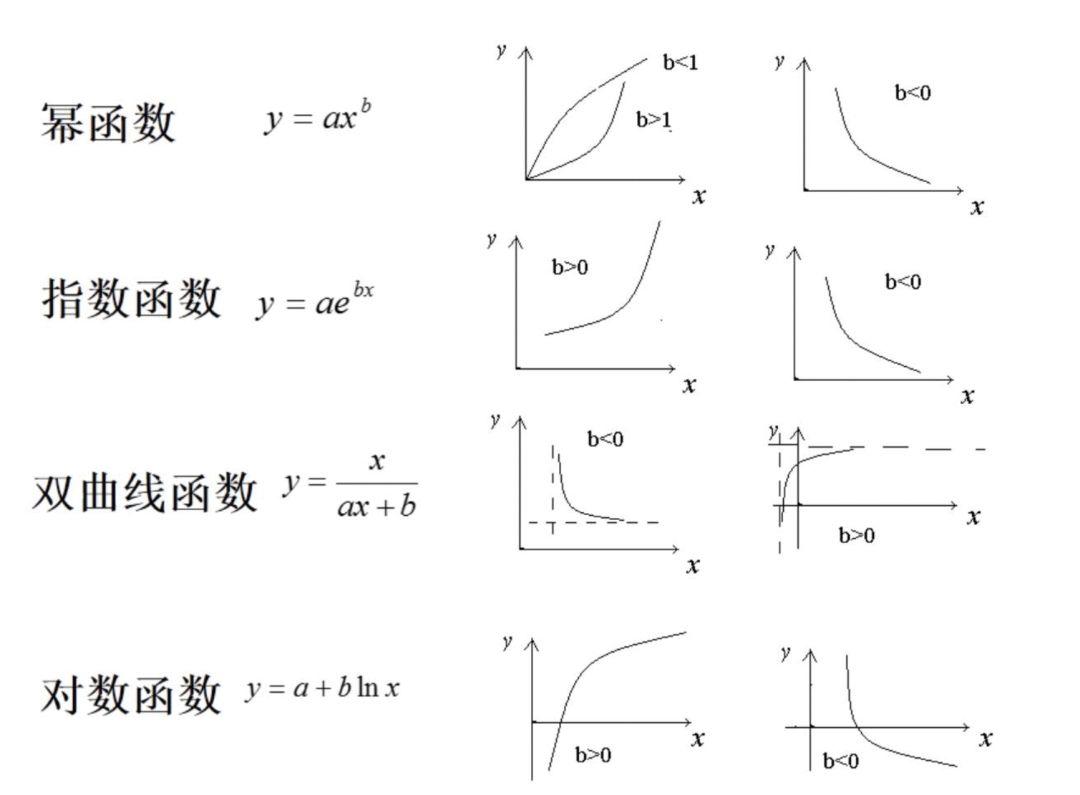
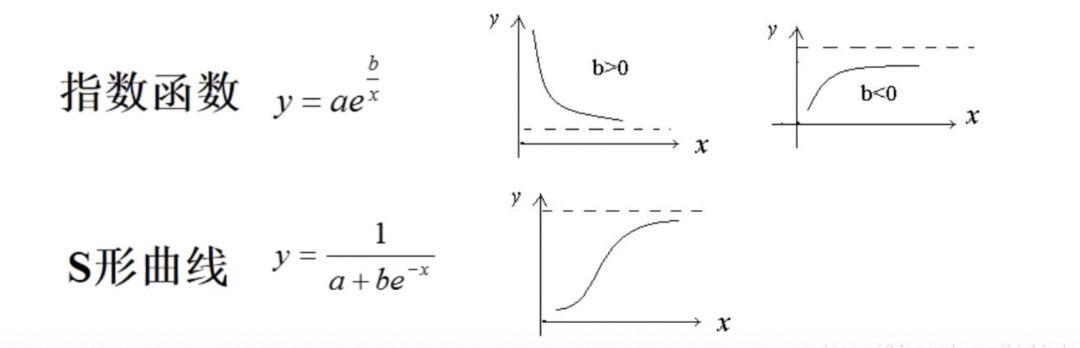
这里离散数据的分布规律与S形曲线大致相同,因此我们采用S形曲线的函数模型进行拟合,假定函数的表达式为:
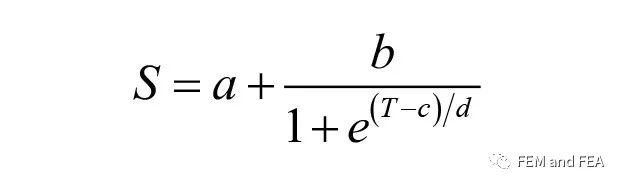
下面采用Matlab进行非线性函数拟合,首先输入原始离散数据点。
Data_T=[25 230 358 452 567 704 900]; %实测温度Data_S=[405 385.1 352 332 151 45 13.4]; %实测屈服应力
在Matlab中,非线性拟合采用函数nlinfit完成,调用语法为:
beta=nlinfit(X,Y,modelfun,beta0)其中X和Y为用于拟合的离散数据点,modelfun为自定义的非线性函数的句柄,beta0为函数预估的系数,beta为拟合得到的非线性函数的系数。
非线性函数的句柄采用函数inline定义,注意到由于本文定义的函数具有4个未知系数,因此beta0为一个数组,故在构造函数表达式时需要用到点除运算。采用函数nlinfit进行拟合时还需要给定非线性函数系数的预估值,不同的取值可能会对拟合效果产生影响,这里本文将系数a取值为离散数据中的最大屈服应力,系数b取值为离散数据中的屈服应力范围,系数c和系数d分别取值为500和50。
func=inline('beta(1)+beta(2)./(1+exp((T-beta(3))/beta(4)))','beta','T'); %定义非线性函数beta0=[max(Data_S) (max(Data_S)-min(Data_S)) 500 50]; %非线性函数系数预估值beta=nlinfit(Data_T,Data_S,func,beta0); %非线性函数拟合
beta即为返还的拟合得到的非线性函数的系数,由此即可得到不同温度对应的初始屈服应力。本文假定模型计算的温度范围为0到1200˚C,通过Matlab可以绘制由离散数据点构成的散点图以及拟合的函数曲线。
T=0:25:1200; %计算温度范围S=beta(1)+beta(2)./(1+exp((T-beta(3))/beta(4))); %拟合得到的初始屈服应力scatter(Data_T,Data_S) %绘制散点图hold onplot(T,S) %绘制非线性函数曲线
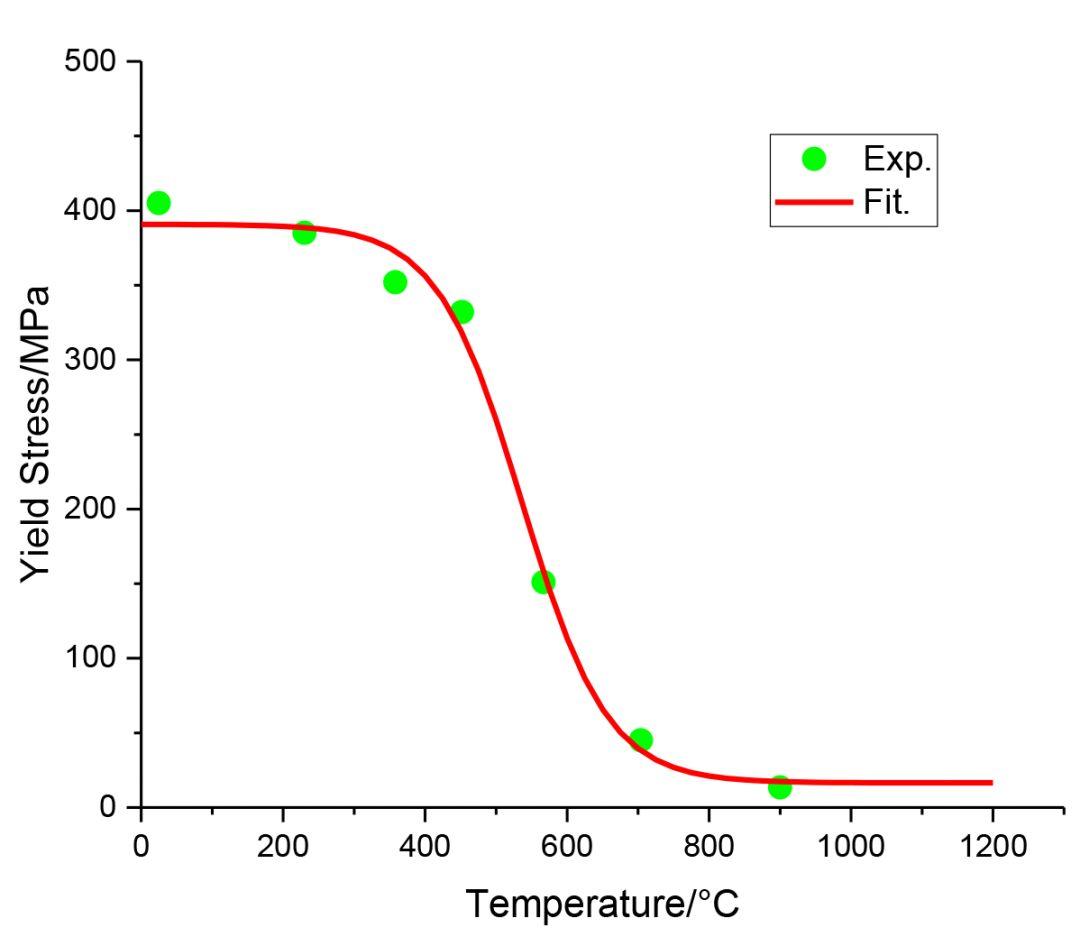
离散数据点及拟合得到的函数曲线
从图中可以看出本文给出的函数模型能较好地拟合离散点数据,函数nlinfit还可以返还拟合函数的均方差值(MSE),用于判断拟合效果,具体调用语法可以参考Matlab帮助文件。事实上,通过函数nlinfit可以实现任意函数的拟合,用来解决有限元计算中的材料参数拟合是非常方便的。




