基于外推法的应力强度因子的计算-1
计算应力强度因子(stress intensity factor, SIF)是断裂力学最为重要的任务之一。在断裂力学的研究过程中,学者们提出了各种用于计算应力强度因子的解析公式,这些公式对于帮助人们认识和应用断裂力学起到了巨大的作用。但由于实际工程结构中裂纹体几何的复杂性,在简单几何下推导得到的解析公式很难满足实际运用需求。随着有限元的发展,采用数值方法来求解应力强度因子成为了可能。
计算应力强度因子最为直观的早期方法是通过有限元法计算裂纹尖端的应力场分布,随后利用裂纹尖端前沿的单元应力或裂纹尖端后方的张开位移(crack open displacement, COD)来计算应力强度因子。若采用裂纹尖端前沿的单元应力来进行计算,则称为基于单元应力的外推法;若采用裂纹后方的张开位移来计算,则称为基于节点位移的外推法。这种数值计算方法的优点为计算简单直观,但需要在裂纹尖端划分足够细密的网格才能得到精确的裂纹尖端应力场和位移场的分布。通常在商业有限元软件中,为了减少单元数量会直接在裂纹尖端布置奇异单元(singular element)或折叠单元(collapsedelement),但建立这种单元所需要的前处理较为复杂,且不便于运用裂纹扩展中。本文为了简单起见,直接在裂纹尖端采用常规单元进行计算。
1. 基本断裂模式
断裂力学将裂纹体的断裂模式归类为三个基本的类型:张开型断裂(I型断裂)、滑移型断裂(II型断裂)和撕裂型断裂(III型断裂)。三种断裂模式如图1.1所示。I型断裂是裂纹体断裂最为主要和常见的断裂模式。I型裂纹和II型裂纹为面内裂纹,而III型裂纹为面外裂纹。实际工程结构的断裂模式并不总是单独以上述的某一种基本断裂模式出现,而可能是三种基本断裂模式的组合。
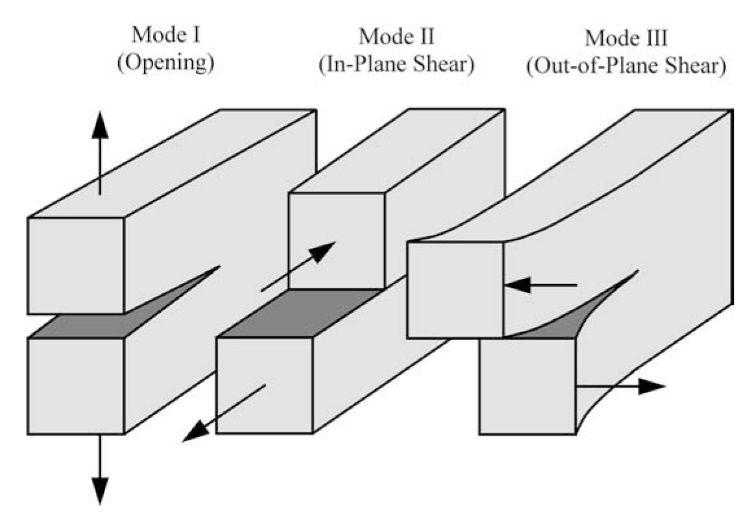
图1.1 三种基本断裂模式
2. 有限宽中心裂纹板应力强度因子计算
本文考虑一有限宽中心裂纹板,板的半宽W=100mm,半高H=200mm,板厚B=1mm,半裂纹长度为20mm。该板在远端承受有均匀的拉伸应力σ=30MPa,如图2.1所示。材料的弹性模量为E=200GPa,泊松比υ=0.25。下面分别采用基于单元应力和节点位移的外推法来计算裂纹尖端的应力强度因子,并与采用解析公式计算得到的解析解进行对比。
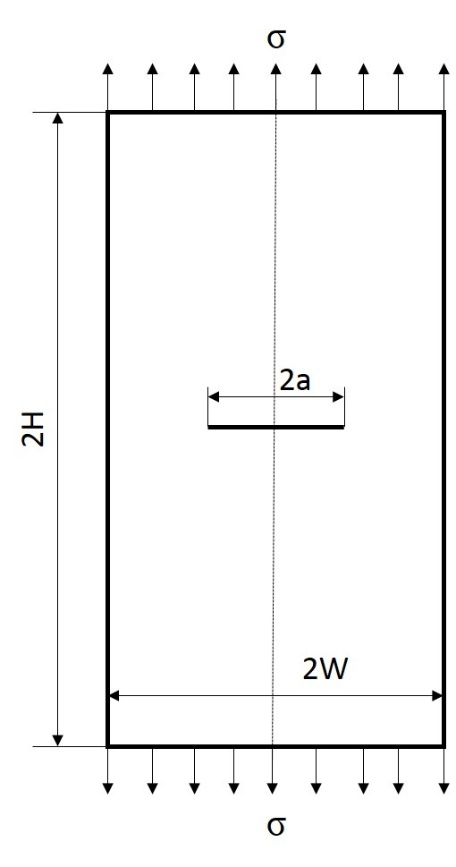
图2.1 有限宽中心裂纹板尺寸
2.1 有限元模型建立
由于该结构具有对称性,因此在建立有限元模型时仅建立了四分之一模型,并在对称面上施加有对称约束。整个模型采用1mm的网格尺寸进行划分,在半裂纹长度上划分有二十个单元。全模型共划分单元40000个,节点40604个。由于在计算应力强度因子时需要提取裂纹尖端前沿的单元应力和裂纹尖端后方的节点位移,对于裂纹面上的单元我们进行了单独编号,将该区域的单元编号与其他的区域单元进行区分,便于该区域单元数据的输出。由于该模型的板厚仅为1mm,因此在计算时采用平面应力单元。最终的有限元模型和边界条件如图2.2所示。
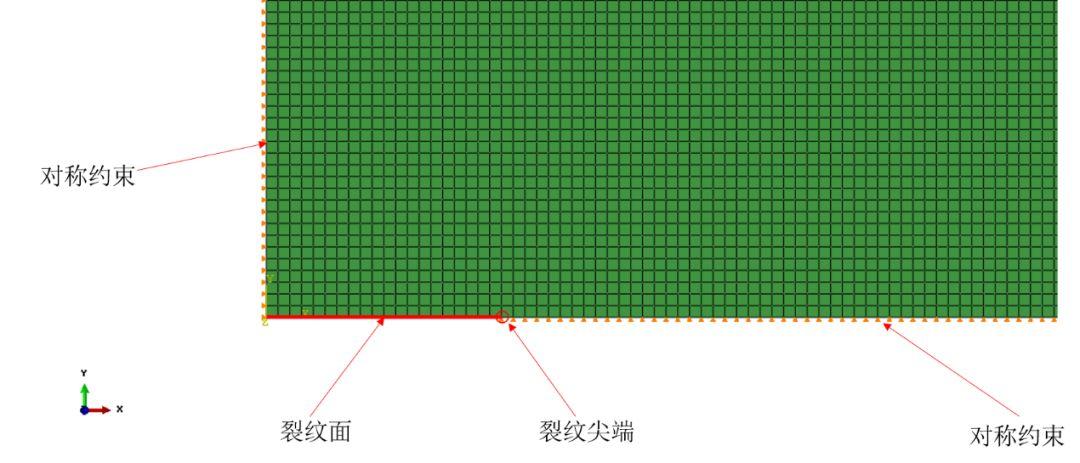
图2.1 有限元模型及边界条件
图2.2中红线区域即为裂纹面,模型对称面上施加有对称约束,在模型远端(图中未标出)承受有均匀的拉伸应力。
2.2 应力强度因子
对于线弹性材料,由于裂纹尖端存在奇异性,裂纹尖端处的应力理论上是无穷大的。因此,在有限元计算中,裂纹尖端的应力值将依赖于网格的尺寸,随着网格尺寸的减小,裂纹尖端的应力值也会升高。因此在研究裂纹问题时不能采用应力值作为研究参数。而应力强度因子的本质实质上就是裂纹尖端奇异性严重程度的反映。
图2.3表示沿X方向的裂纹尖端前沿的应力分量。
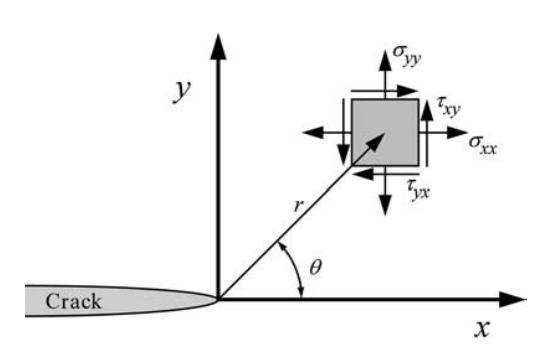
图2.3 裂纹尖端前沿应力分量
对于本文中的中心裂纹板,其断裂模式为张开型断裂(I型断裂),其对应的I型应力强度因子KI可表示为:
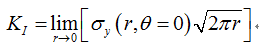
式中σy为垂直于裂纹面方向的应力分量,r为距离裂纹尖端的极半径,θ为相对于裂纹方向(X轴)的极角。
KI也可以采用裂纹尖端后方(裂纹面)上垂直于裂纹面的位移分量(裂纹张开位移,COD)来计算:
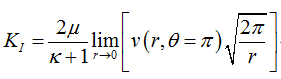
式中μ为剪切模量,κ为膨胀模量,对于平面应力问题,κ=(3-v)/(1+v),对于平面应变问题,κ=3-4v。
2.3 基于单元应力的外推法
从上面的I型应力强度因子的表达式可以看出,I型应力强度因子的取值与裂纹尖端的垂直于裂纹面的应力分量σy的取值有关,但我们知道,理论上裂纹尖端的应力值是趋近于无穷大的。因此通过有限元计算得到裂纹尖端的应力值并非其真实值。虽然裂纹尖端处(r=0)对应的应力值我们无法直接从有限元中得到,但裂纹尖端前沿的那些非奇异的应力值却是已知的。假设裂纹尖端前沿ri处的应力值σy可以计算得到,则其对应的I型应力强度因子可以表示为:
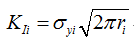
通过这些数据对,我们可以利用最小二乘法拟合出I应力强度因子KI与裂纹尖端前沿距离r之间的线性关系,最后外推得到裂纹尖端(r=0)处对应的应力强度因子。
通过商业有限元软件ABAQUS我们计算得到裂纹尖端前沿的垂直于裂纹面方向的应力分量σy(S22)的分布如图2.4所示。
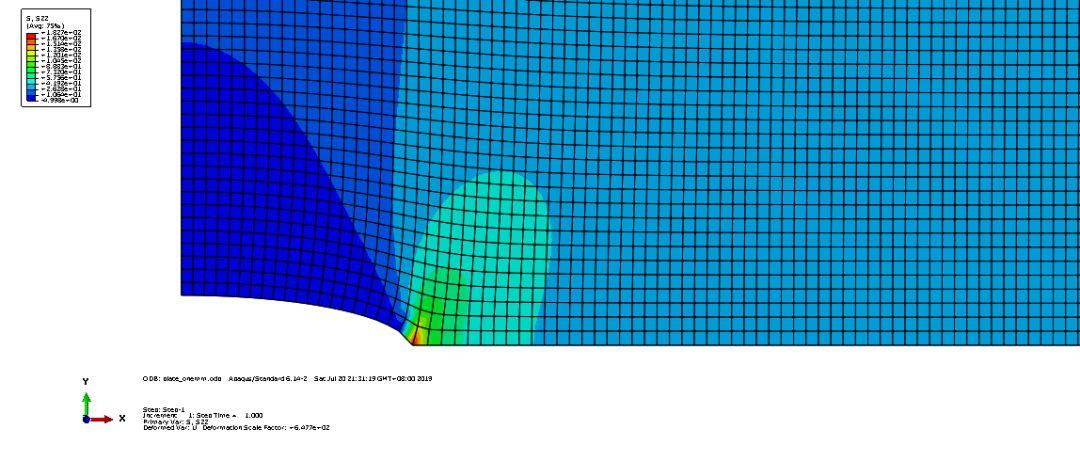
图2.4 裂纹尖端前沿的应力(S22)分布
由于在有限元计算中节点的应力值是通过积分点计算得到的应力值外推得到的。为了获得精确的应力分布,本文提取了裂纹尖端前沿20个单元上的积分点对应的应力值而非节点的应力值,得到裂纹尖端前沿的应力分量σy的分布如图2.5所示。

图2.5 裂纹尖端应力分布
从图2.5中可以看出,裂纹尖端由于存在奇异性因此应力值非常高,而随着距离裂纹尖端的距离越远,其应力值越来越趋近于远场施加的均匀应力。
通过前文所述的方法,获得应力强度因子KI和距离裂尖距离的数据对,并采用最小二乘法进行拟合,得到如图2.6所示曲线。

图2.6 应力强度因子外推
从图2.6可以看出,通过外推法得到的裂纹尖端的I型应力强度因子KI的取值为227.4MPa∙mm1/2,这与有限宽中心裂纹板的解析值243.6 MPa∙mm1/2非常接近。实际上,该曲线在接近裂纹尖端时已经不再满足线性假设,因此剔除裂纹靠近裂纹尖端的数据对后将获得更接近于解析解的应力强度因子取值。
2.4 基于节点位移的外推法
采用与前文相似的方法,也可以采用节点位移来进行外推。假设裂纹尖端后方距离为ri处的垂直于裂纹面方向的位移分量为vi,则对应的I型应力强度因子KIi可以表示为:

我们在ABAQUS中创建一条沿着裂纹面的路径,如图2.7所示。

图2.7 提取裂纹张开位移
将提取到的位移分量按上述方法处理得到对应的I型应力强度因子,并采用最小二乘法进行拟合得到图2.8所示曲线。
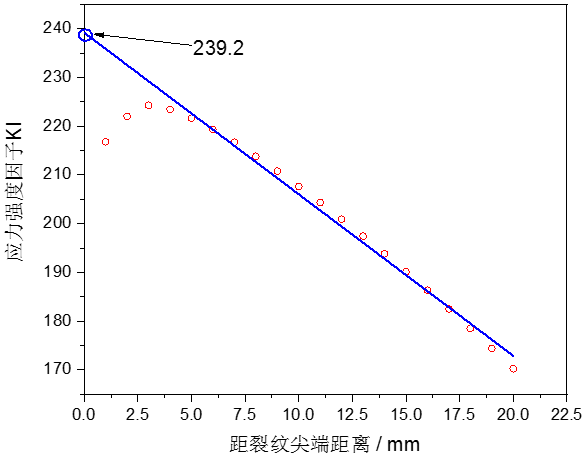
图2.8 应力强度因子外推
从图2.8可以看出通过外推法得到裂纹尖端的I型应力强度因子为239.2 MPa∙mm1/2,相比于基于单元应力的外推法,计算得到的结果要更接近于解析值。同时,在使用节点位移进行外推时裂纹尖端也不再满足线性关系,因此剔除裂纹尖端附近的数据对后将得到更好的拟合效果。
总的来说,采用外推法来计算应力强度因子较为简单直观,但也存在诸多缺点。如在裂纹尖端需要采用细密的网格来保证计算精度。虽然采用奇异单元或折叠单元可以减少网格数量,同时保证裂纹尖端的计算精度,但前处理过程较为复杂。同时,在靠近裂纹尖端的区域无法满足线性关系,在剔除裂尖附近的数据反而增加了计算精度,而本身应力强度因子就是裂纹尖端奇异性的反映,因此这两者之间存在一定矛盾。
本文相关算例和计算方法参考了《断裂力学中的数值计算方法及工程应用》一书。




