基于DFLUX的焊接双椭球热源模拟

1年前浏览1506

1. 双椭球热源模型

双椭球热源是焊接仿真中最为常用的热源模型，本文基于ABAQUS用户子程序DFLUX建立了双椭球热源模型，并对焊接过程中的温度场进行模拟。双椭球热源模型含有两个形状并不完全相同的椭球体，前后两个椭球体具有不同的热流密度分布，前半部分椭球体的热流密度分布可以表示为：

式（1）

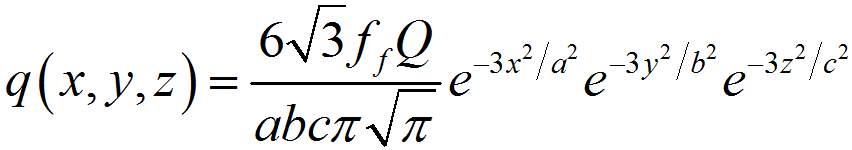
后半部分椭球体的热流密度分布可以表示为：

式（2）

式中a，b，c为椭球体的半长，对于前后两个椭球体，a，b，c相互独立，可以取不同的值，f_f和f_r为前后两个椭球的能量分配系数，必须满足：

式（3）

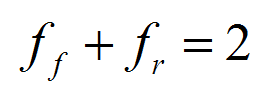
式（1）和式（2）中Q为总的焊接热流密度，可以表示为：

式（4）

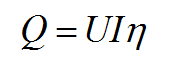
其中U为焊接电压，I为焊接电流，η为焊接效率。

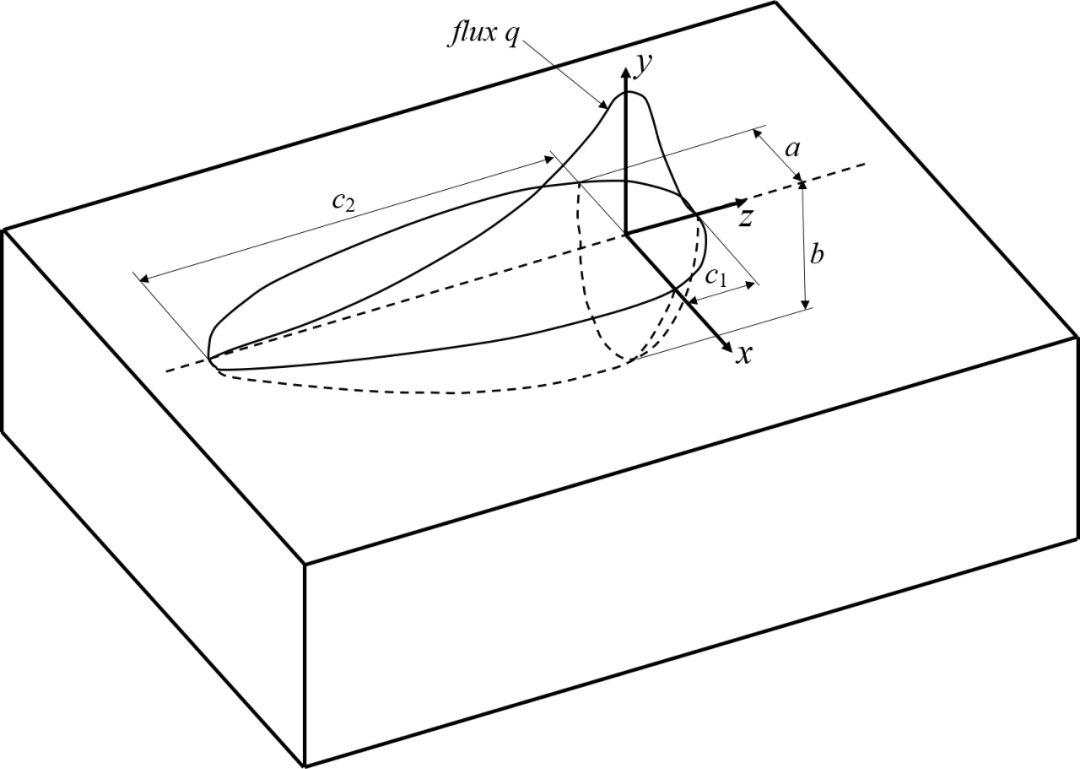
需注意上面关于热流密度分布的表达式采用的是以热源中心为坐标原点的局部坐标系，相应的坐标定义如图1所示。

图1 双椭球热源坐标系

2. 低碳钢厚板焊接温度场模拟

2.1 厚板有限元模型及材料属性

本文以低碳钢厚板的焊接过程为例，对焊接过程中的温度场进行模拟，模拟过程中仅考虑焊接热源产生的温度场，不考虑焊接产生的残余应力场以及生死单元的模拟。分析采用的厚板长度为40cm，宽度为20cm，厚度为10cm，考虑到模型具有对称性，因此仅建立1/2有限元模型，如图2所示。

图2 焊接厚板有限元模型

在焊接厚板的有限元模型中，厚板的全局坐标系设定在焊接的起始端，并假设焊接沿着Z向进行，图2中的网格加密区域为焊接热源作用的区域。焊接热源以及焊接过程中的相关参数如表1所示。

表1 焊接热源参数

由于焊接过程中产生的高温将会使得材料属性产生波动，因此将材料属性考虑为随温度变化，其导热系数和比热容如图3和图4所示。

图3 导热系数随温度变化

图4 比热容随温度变化

2.2 用户子程序的实现

从式（1）和式（2）可以看出，模拟焊接热源的关键在于如何构造一个满足双椭球形状的热流密度分布，在ABAQUS中对于任意分布的热流密度载荷可以通过用户子程序DFLUX来实现。当使用用户子程序DFLUX模拟焊接热源时，在每个单元积分点上用户子程序DFLUX都将被调用，而该积分点的坐标将会被传递到用户子程序DFLUX中，通过建立积分点坐标与热流密度之间的联系，即可实现对于任意焊接热源的模拟，具体实现思路如下：

（1）读取当前积分点的坐标COORDS(3);

（2）根据当前时间与焊接热源中心的初始位置计算当前焊接热源中心的坐标，本文中假设焊接沿着Z向进行，由于模型的全局坐标位于焊接的起始端，因此任意时刻的热源中心的坐标可表示为：

式（5）

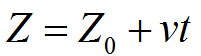
其中Z₀为焊接热源中心在起始时刻的坐标，v为焊接速度，t为焊接时间，对于沿着任意方向的焊接也可以采用同样的方式；

（3）通过当前积分点坐标与焊接热源中心的坐标可以得到积分点在以焊接热源中心为原点的局部坐标系中的局部坐标：

式（6）

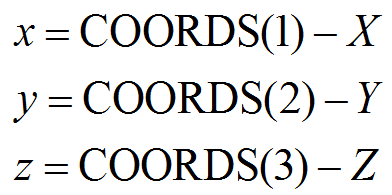
其中x，y，z为积分点在焊接热源局部坐标系中坐标，COORDS(1)，COORDS(2)，COORDS(3)为积分点的全局坐标，X，Y，Z为当前热源中心的全局坐标；

（4）通过几何关系判断当前积分点是否位于双椭圆热源内部，判断条件为：

式（7）

（5）若积分点没有位于两个椭球内，则当前积分点的热流密度FLUX（1）等于零，若位于任意一个椭球内，则根据式（1）或式（2）计算相应的热流密度。

完整的子程序如下：

     SUBROUTINE DFLUX(FLUX,SOL,KSTEP,KINC,TIME,NOEL,NPT,COORDS,     1 JLTYP,TEMP,PRESS,SNAME)C      INCLUDE 'ABA_PARAM.INC'C      DIMENSION FLUX(2), TIME(2), COORDS(3)      CHARACTER*80 SNAME
C     程序用于模拟焊接双椭球热源C     程序采用国际单位制      C     **********焊接参数定义*************      REAL,PARAMETER::WELD_VOLTAGE=32.9                !焊接电压      REAL,PARAMETER::WELD_CURRENT=1170                !焊接电流      REAL,PARAMETER::WELD_EFFICIENCY=0.95             !焊接效率      REAL,PARAMETER::WELD_SPEED=0.005                 !焊接速度      C     **********焊接椭球参数定义**********      REAL,PARAMETER::AXES_A=2e-2                      !椭球半轴a      REAL,PARAMETER::AXES_B=2e-2                      !椭球半轴b      REAL,PARAMETER::AXES_C1=1.5e-2                   !前椭球半轴c1      REAL,PARAMETER::AXES_C2=3e-2                     !后椭球半轴c2      C     *********热量分配比定义*************C     ff与fr之和必须等于2      REAL,PARAMETER::HEAT_FRACTION_F=0.6              !前椭球的热量分配      REAL,PARAMETER::HEAT_FRACTION_R=1.4              !后椭球的热量分配      C     *********焊接热源中心初始坐标定义*****      REAL,PARAMETER::WELD_CENTER_X_INITIAL=0          !焊接热源中心初始坐标x      REAL,PARAMETER::WELD_CENYER_Y_INITIAL=0          !焊接热源中心初始坐标y      REAL,PARAMETER::WELD_CENTER_Z_INITIAL=5e-2       !焊接热源中心初始坐标z            REAL,PARAMETER::PI=3.1415926      C     ********局部坐标变量定义*************      REAL::LOCAL_X        !局部坐标x，对应于全局坐标x和椭圆半轴a      REAL::LOCAL_Y        !局部坐标y，对应于全局坐标y和椭圆半轴b(焊接深度方向)      REAL::LOCAL_Z        !局部坐标z，对应于全局坐标z和椭圆半轴c(焊接前进方向)      C     ********定义热源中心坐标*************C     热源中心将沿着焊接方向移动，通过热源中心的全局坐标可确定局部坐标      REAL::WELD_CENTER_X     !热源中心全局坐标x      REAL::WELD_CENTER_Y     !热源中心全局坐标y      REAL::WELD_CENTER_Z     !热源中心全局坐标z      C     定义总热量输出      REAL::QC     定义标志符,判断积分点是否位于热源内            INTEGER::IS_IN           C     测试变量      REAL::R1,R2      C     *******开始计算各个积分点处的热流密度**********C     计算单位时间总的焊接热量输入      Q=WELD_VOLTAGE*WELD_CURRENT*WELD_EFFICIENCYC     计算当前热源中心初始坐标(焊接沿z向进行)      WELD_CENTER_X=WELD_CENTER_X_INITIAL      WELD_CENTER_Y=WELD_CENTER_Y_INITIAL      WELD_CENTER_Z=WELD_CENTER_Z_INITIAL+WELD_SPEED*TIME(1)C     计算当前积分点在焊接热源中的局部坐标      LOCAL_X=COORDS(1)-WELD_CENTER_X      LOCAL_Y=COORDS(2)-WELD_CENTER_Y      LOCAL_Z=COORDS(3)-WELD_CENTER_Z      C     判断积分点是否位于前椭球内           IF((LOCAL_X**2/AXES_A**2+LOCAL_Y**2/AXES_B**2+     &  LOCAL_Z**2/AXES_C1**2).LE.1)THEN                    IF(LOCAL_Z.GE.0)THEN              IS_IN=1           !积分点位于前椭球内                           ELSE              IS_IN=0          END IF      ELSE          IS_IN=0      END IFC     判断积分点是否位于后椭球内      IF((LOCAL_X**2/AXES_A**2+LOCAL_Y**2/AXES_B**2+     &  LOCAL_Z**2/AXES_C2**2).LE.1)THEN            IF(LOCAL_Z.LE.0)THEN              IS_IN=2          !积分点位于后椭球内          ELSE              IS_IN=0          END IF      ELSE          IS_IN=0      END IF      C     计算积分点处的热流密度      IF(IS_IN.EQ.0)THEN              !积分点没有位于双椭球热源内          FLUX(1)=0      ELSE IF(IS_IN.EQ.1)THEN         !积分点位于前椭球热源内          FLUX(1)=6*1.732*HEAT_FRACTION_F*Q/(AXES_A*AXES_B*     &    AXES_C1*PI*SQRT(PI))*EXP(-3*(LOCAL_X)**2/(AXES_A)**2)*     &    EXP(-3*(LOCAL_Y)**2/(AXES_B)**2)*     &    EXP(-3*(LOCAL_Z)**2/(AXES_C1)**2)      ELSE IF(IS_IN.EQ.2)THEN         !积分点位于后椭球热源内          FLUX(1)=6*1.732*HEAT_FRACTION_R*Q/(AXES_A*AXES_B*     &    AXES_C2*PI*SQRT(PI))*EXP(-3*(LOCAL_X)**2/(AXES_A)**2)*     &    EXP(-3*(LOCAL_Y)**2/(AXES_B)**2)*     &    EXP(-3*(LOCAL_Z)**2/(AXES_C2)**2)       ELSE          FLUX(1)=0      END IF          
      RETURN      END

3. 计算结果

计算得到的双椭球热源在焊接过程中形成的温度场如图5所示，假设材料的熔点为1400ºC，图5中的灰色区域可近似代表熔池的形状。

图5 焊接温度场

在焊接过程的不同时刻，沿焊接方向的温度分布如图6所示。

图6 不同时刻沿焊接方向的温度分布变化

从图6可以看出，在焊接的初始时刻，沿焊接方向的温度分布与双椭球热源的热流密度分布基本一致，随着焊接过程的进行，热源中心的温度急剧上升，并且热源中心开始沿着焊接方向移动。

对于本文建立的厚板焊接的有限元模型，Goldak¹给出了试验获得的熔池和热影响区的尺寸，对于熔池，试验获得的长度为1.4cm，对于热影响区，试验获得的尺寸为2.1cm。Goldak假设温度高于723ºC的区域为热影响区，温度高于1480ºC的区域为熔池区域。对于本文的模型，当焊接过程中熔池形状趋于稳定后计算得到的熔池和热影响区的形貌如图7所示，可以看出模拟给出的熔池尺寸约为1.2cm，热影响区尺寸约为1.8cm，计算结果与试验结果是非常接近的。在本文的模型中并没有考虑到焊接平板表面的对流和辐射效应，因此与Goldak给出的仿真结果有一定差异，但仍然取得了较好的模拟效果。

图7 熔池和热影响区形貌

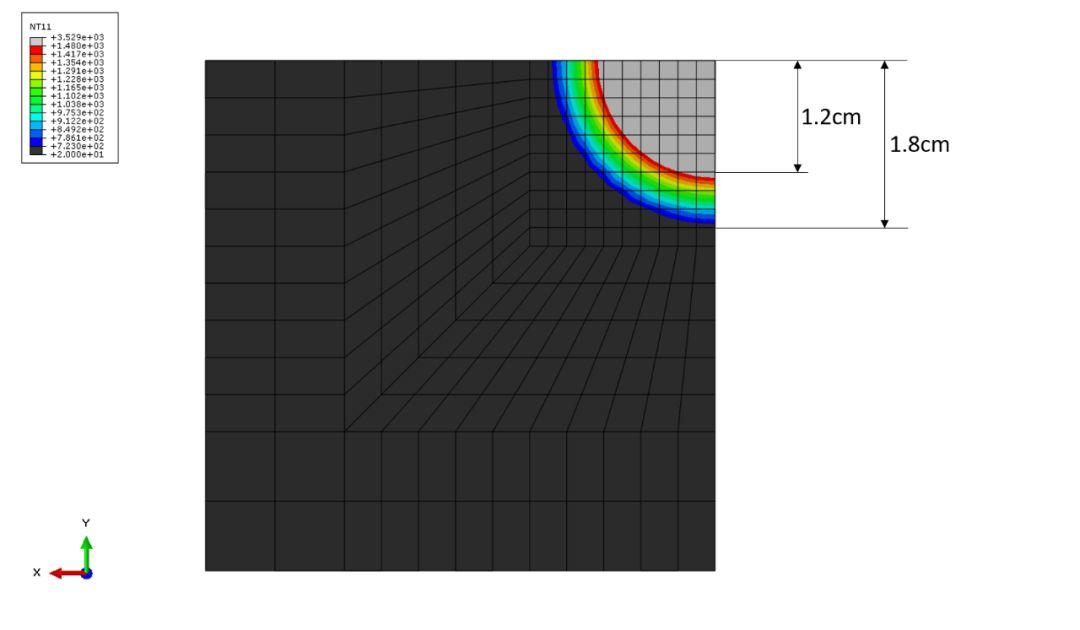
此外，本文对于焊接过程的模拟没有考虑焊缝材料的融化，而通过ABAQUS的脚本编写或者用户子程序USDFLD可以实现对于单元生死的模拟，则可能会取得更好的模拟效果。

参考文献

[1] Goldak, J., Chakravarti, A., &Bibby, M. A new finite elementmodel for welding heat sources. Metallurgical transactions B, Vol. 15(2),pp.299-305,1984.

来源：FEM and FEA

ACT 焊接材料试验

著作权归作者所有，欢迎分享，未经许可，不得转载

首次发布时间：2023-05-30