基于权函数法的表面裂纹扩展寿命计算

1. 简介

表面裂纹通常萌生并扩展于工程结构的缺口，孔洞及焊接接头处。这些工程构件绝大部分的有用寿命都将消耗在表面裂纹的扩展过程中。因此，精确计算表面裂纹的扩展寿命对于预测这些构件的剩余寿命具有重要的意义。目前，基于断裂力学的评估方法一般采用应力强度因子来评估表面裂纹，而应力强度因子的计算可采用有限元法(FEM, Finite Element Method)来完成。Newman和Raju通过有限元法获得了有限厚度的平板中半椭圆表面裂纹的应力强度因子解¹，可采用如下所示的经验公式来描述，但该公式仅适用于承受远端拉伸应力或弯曲应力的平板。

其中a为表面裂纹深度，c为半裂纹长度，φ为椭圆的参数角，B为平板宽度，T为平板厚度，相关的几何参数如图1-1所示。F和H为边界修正系数,Q为第二类完整椭圆积分，可近似表示为：

由于上述公式只适用于平板承受远端拉伸或弯曲应力的情况，因此具有很大的局限性。对于更为复杂的应力分布，常用的方法为有限元法或权函数法(WFM, Weight Function Method)。尽管有限元法可以处理任意应力分布下的应力强度因子计算，但建立带表面裂纹的复杂构件的有限元模型并完成应力强度因子的评估，仍然是一件非常繁琐的工作。

本文将首先介绍基于权函数法的应力强度因子的计算方法，并与通过有限元法得到的高次应力分布下表面裂纹的应力强度因子值进行对比，验证权函数法的计算精度，随后基于Paris公式，完成表面裂纹扩展寿命的预测，并与断裂分析软件Franc3D的计算结果进行对比。

2. 基于权函数法的应力强度因子计算

2.1 权函数法

对于线弹性材料，应力，应变以及位移均具有叠加性。同样的，只要构件的加载方式没有发生改变，应力强度因子也具有叠加性，即：

需要指出的是，这并不意味着不同断裂模式下的应力强度因子具有叠加性，即：

但能量释放率G仍然具有叠加性：

在许多情况下，利用叠加原理可以实现通过简单应力分布下的应力强度因子解来实现对复杂应力分布下应力强度因子的求解。例如，考虑一个具有角裂纹的平板，该平板同时承受轴向载荷P_m和三点弯曲载荷P_b的作用，由于这两种加载模式均对应I型断裂模式，因此I型应力强度因子K_I具有叠加性：

其中f_m和f_b分别为轴向加载和弯曲加载下的几何修正系数。

下面考虑一个承受有远端拉伸面力P(x)作用的无裂纹体，如图2-1所示，该远端拉伸应力将会在无裂纹体内部的A-B平面上产生正应力分布p(x)，为了使裂纹满足I型断裂模式，假设A-B平面上无剪切应力作用。现在假设在A-B平面上形成了一条裂纹，并且裂纹体仍然作用有远端面力P(x)，如图2-2(a)所示，如果我们移除远端应力的作用，并在裂纹面上施加拉伸面力p(x)(图2-2(c)),则由叠加原理可知K_I保持不变。这是由于在图2-2(c)所示情况中，裂纹面上作用的压应力将使得裂纹完全闭合，因此其应力强度因子K_I^(c)=0。

图2-1 无裂纹体承受远端任意面力P(x)作用，在A-B平面上形成正应力分布p(x)

图2-2 叠加原理的应用

从上式中可以看出，远端承受面力P(x)作用的裂纹体与裂纹面上承受有面力p(x)的裂纹体具有相同的应力强度因子。

权函数法 正是基于叠加原理得到的。当我们去推导一个裂纹体的应力强度因子时，该应力强度因子对应的是该结构特定的一组边界条件，不同的载荷条件将产生不同的应力强度因子值。然而，即使是一组特定的边界条件，其已经具有足够的信息帮助我们求解任意其他边界条件下的应力强度因子值。

下面，考虑一个处于平面应力或平面应变状态的裂纹体，在该裂纹体上分别施加两种任意的载荷条件，为了简化起见，假设载荷关于裂纹面完全对称，则裂纹体完全处于I型断裂模式。若我们已知载荷条件(1)下的应力强度因子值K_I⁽¹⁾，并希望求得载荷条件(2)下的应力强度因子值K_I⁽²⁾，Rice的推导表明两种应力强度因子值满足以下关系²：

其中Γ和A分别为裂纹体的周长和面积，u_i为x和y方向的位移。由于载荷条件(1)和(2)是任意的，因此K_I⁽²⁾并不依赖于K_I⁽¹⁾和u_i⁽¹⁾。因此函数

其中x_i代表坐标x和y，必须完全不依赖于载荷条件(1)。Bueckner先于Rice两年得到了相同的结果，并将h称为权函数³。

权函数h只取决于裂纹体的几何，因此只要裂纹体的几何是固定的，就能够得到任意边界条件下的应力强度因子。并且，通过前面的叠加原理已经表明任意载荷条件下的应力强度因子计算均可通过在裂纹面上施加合适的面力进行等效。因此，二维裂纹体的I型应力强度因子K_I可表示为：

其中p(x)为裂纹面上承受的面力（等于无裂纹体上沿虚拟裂纹面的正应力），Γ_c为裂纹长度。从上式中可以看出，权函数h(x)的实质为在裂纹面上x作用有一个单位集中力时的应力强度因子值，而上式中的积分可以看作是将沿裂纹面上所有离散集中力的应力强度因子值进行累加。

对于一个含有表面裂纹的有限厚度平板，假设在平板厚度方向上作用有一维的任意应力分布，则基于权函数法的表面裂纹最深点A和表面点C处的应力强度因子值可表示为：

其中σ(x)为沿厚度方向的应力分布，m^A(x;a,c)和m^C(x;a,c)分别为最深点A和表面点C的权函数。

对于最深点A，其统一形式的权函数可表示为：

常数M₁，M₂和M₃可表示为：

其中Q为第二类完整椭圆积分。Y₀和Y₁为裂纹深度a，裂纹半长c以及板厚T的影响系数。

当裂纹形状比满足0.0≤a/c≤1.0，Y₀和Y₁可分别表示为⁴：

当裂纹形状比满足1.0≤a/c≤2.0，Y₀和Y₁可分别表示为⁵：

对于最深点C，其统一形式的权函数可表示为：

常数N₁，N₂和N₃可表示为：

其中Q为第二类完整椭圆积分。F₀和F₁为裂纹深度a，裂纹半长c以及板厚T的影响系数。

当裂纹形状比满足0.0≤a/c≤1.0，F₀和F₁可分别表示为⁴：

当裂纹形状比满足1.0≤a/c≤2.0，F₀和F₁可分别表示为⁵：

通过上述公式即可利用权函数法计算表面裂纹的应力强度因子。由于在计算过程中涉及到积分运算，对于复杂的应力分布，一般可采用数值方法进行求解，具体的数值积分方法可参见《基于权函数法的应力强度因子计算》。

2.2 应力强度因子验证

为了验证基于权函数法的表面裂纹应力强度因子的计算精度，分别在裂纹面上施加如下所示的四种应力分布：

其中σ₀为名义应力，a为裂纹长度。四种应力分布如图2-3所示。

图2-3 施加在裂纹面上的应力分布

Shiratori和Wang、Lamber等人分别采用有限元法计算得到了表面裂纹形状比a/c取0.05,0.1,0.2,0.4,0.6,1.0,1.5和2.0，a/T取0.2,0.8,0.6,0.8时表面裂纹最深点和表面点处的应力强度因子值，在本文中可供参考。需要注意的是，在这些有限元模型中平板的宽度足够大，平板宽度对应力强度因子的影响非常小，即有限宽度修正系数f_b趋近于1。

采用下面的公式对应力强度因子进行归一化处理：

F为边界修正系数，Q为第二类完整椭圆积分。

最终可得到不同应力分布下权函数法和有限元法计算得到的应力强度因子对比如图2-4至2-7所示。

图2-4常应力分布下(a)最深点,(b)表面点处权函数法和有限元法计算得到的边界修正系数对比

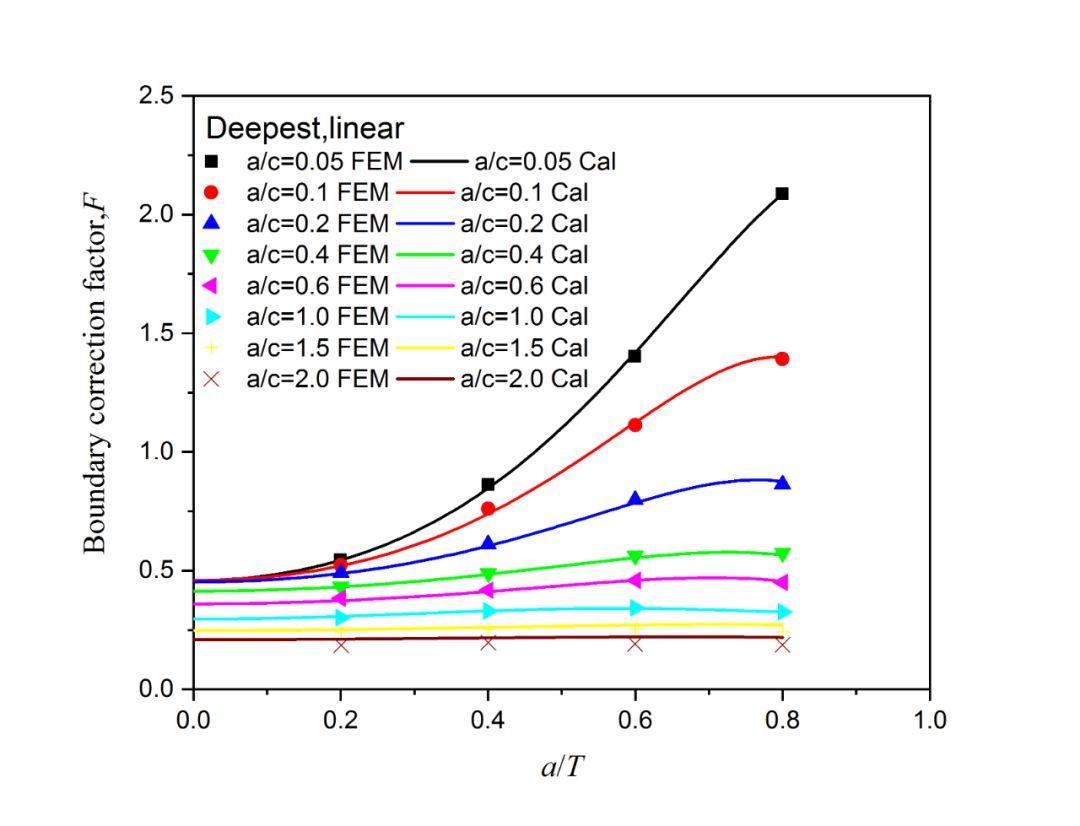
图2-5线性应力分布下(a)最深点,(b)表面点处权函数法和有限元法计算得到的边界修正系数对比

图2-6 二次应力分布下(a)最深点,(b)表面点处权函数法和有限元法计算得到的边界修正系数对比

图2-7 三次应力分布下(a)最深点,(b)表面点处权函数法和有限元法计算得到的边界修正系数对比

从图中可以看出，在0.0≤a/c≤1.0和0.2≤a/T≤0.8的范围内，通过权函数法计算得到的应力强度因子与有限元法的计算结果吻合良好，因此，从工程应用的角度来看，权函数法计算的应力强度因子可以用于进一步的疲劳裂纹扩展分析。

3. 疲劳裂纹扩展寿命预测

恒幅载荷下基于权函数法的表面裂纹扩展寿命预测，可按下述流程完成⁶：

1.通过有限元法对无裂纹体进行静力分析，获得沿虚拟裂纹面上的应力分布σ(x)。

2.定义初始裂纹深度a₀以及半长c₀。

3.根据恒幅载荷谱的载荷幅值Δσ_nom以及应力比R，基于权函数法分别计算当前裂纹深度和长度下对应的最深点A和表面点C处的应力强度因子幅值ΔK^A和ΔK^C。

4.通过Paris公式计算最深点A和表面点C处的裂纹扩展速率：

其中C和m为材料常数。

5.对于给定载荷循环周次ΔN，在该循环周次内裂纹深度和长度方向的扩展增量可分别表示为：

因此新的裂纹深度a_i+1和裂纹半长c_i+1为：

6.随后更新循环周次：

7.重复步骤(3)-(6)直到满足终止条件。

基于上述计算原理，作者通过MATLAB开发了断裂分析软件FCGPP(Fatigue Crack Growth Prediction Program of Welded Joints)用于焊接接头疲劳裂纹扩展寿命的预测，其主界面如图3-1所示。

图3-1 FCGPP主界面

FCGPP支持导入任意的应力分布及焊接过程产生的残余应力分布，通过使用裂纹闭合模型能够考虑应力比对裂纹扩展速率的影响，最终实现对恒幅载荷下焊接接头疲劳裂纹扩展寿命的预测。

3.1 平板表面裂纹扩展寿命预测

为了验证基于权函数法的表面裂纹扩展寿命预测的精度，本文考虑一个最为简单的计算实例，一块有限厚度的平板在远端承受应力幅值Δσ=200MPa，应力比R=0的恒幅载荷的作用。平板初始表面裂纹的深度a₀为1mm，长度2c₀为2mm。平板宽度为100mm，厚度为16mm。计算中取Paris公式的材料常数C为4.5×10^-13MPa∙mm^1/2，m=2.75。循环周次增量ΔN取为200。

对比FCGPP以及断裂分析软件Franc3D计算得到的疲劳裂纹扩展寿命，结果如图3-2所示。

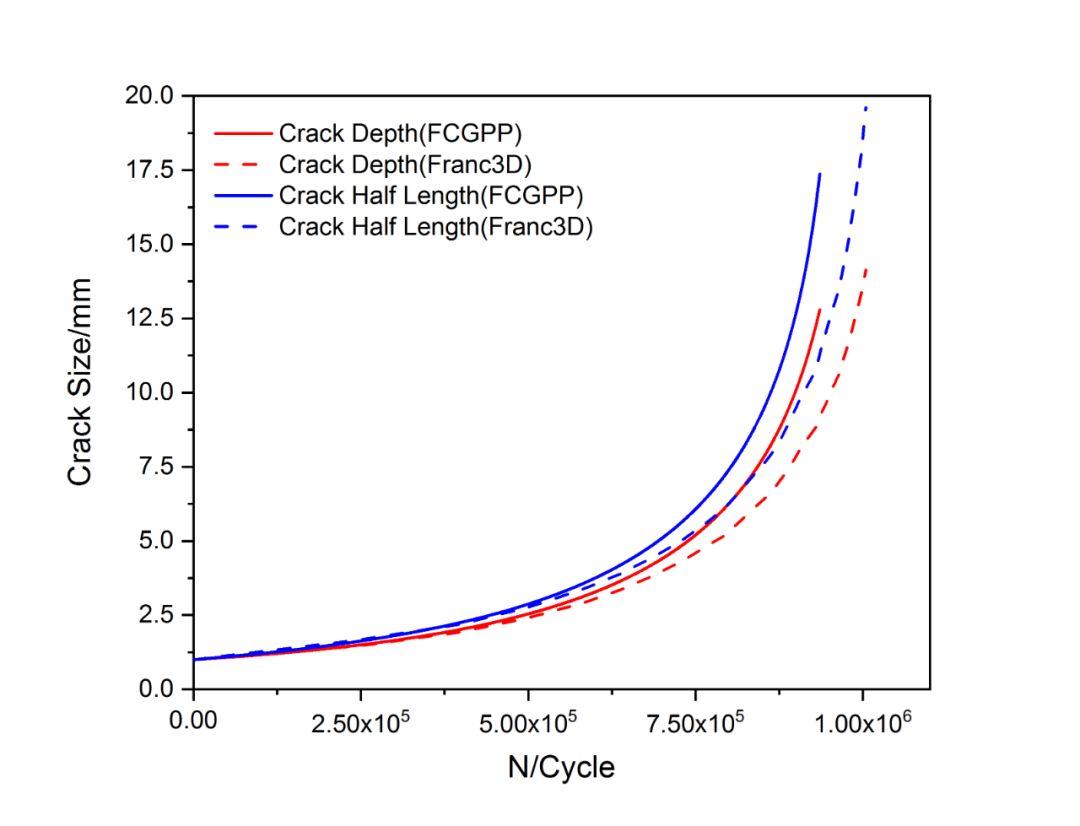
图3-2 疲劳裂纹扩展寿命对比

从图3-2中可以看出，FCGPP与断裂分析软件Franc3D计算得到的疲劳裂纹扩展寿命非常接近，误差仅为5.7%，因此可以认为基于权函数法的表面裂纹扩展寿命预测具有较高的计算精度，完全满足工程应用的要求。

对比FCGPP和断裂分析软件Fracn3D计算的裂纹扩展过程中裂纹最深点A和表面点C的应力强度因子幅值ΔK的变化，结果如图3-3所示。

图3-3 (a)最深点A,(b)表面点C应力强度因子范围对比

从图3-3中可以看出，FCGPP计算的最深点A处的应力强度因子幅值与Franc3D的计算结果非常吻合，但表面点C处的计算结果却相差巨大，这是非常奇怪的现象，因为图3-2中的结果表明FCGPP与Franc3D计算的裂纹扩展寿命非常接近，那么在表面点C处的应力强度因子幅值应该不会有太大的区别。

为了探究出现这一现象的原因，我们提取Franc3D计算得到的裂纹扩展某一时刻裂纹前缘应力强度因子分布并与FCGPP的计算结果进行对比，如图3-4所示。

图3-4 裂纹前缘应力强度因子幅值分布对比

由于权函数法只计算了表面裂纹最深点A和表面点C处的应力强度因子，因此在图3-4中只有三个点。从图3-4中可以发现，Franc3D的计算结果表明在表面裂纹的表面点出现了应力强度因子跌落的现象，导致与FCGPP的计算结果出现了很大的差异。那么这种差异是否是由于网格收敛性或者疲劳裂纹扩展过程中的数值噪声引起的呢？Franc3D Benchmark中同样给出了一个平板中表面裂纹应力强度因子的计算实例，并将计算结果与Raju-Newman公式的计算结果进行了对比。该算例在裂纹前缘采用非常细密的网格进行划分，同样捕捉到了裂纹表面点应力强度因子下降的现象，这证明这种现象是客观存在的，并非由于计算误差引起。

那么，这是否表明权函数法在表面点的计算结果是错误的呢？事实上，在裂纹面与表面自由面交叉点上并不存在r^-1/2的奇异性，r^-1/2的奇异性只存在于完全嵌入材料的裂纹前缘处。对于泊松比v=0.3的工程材料，靠近裂纹表面点处的奇异性为r^-0.4523，因此不再满足r^-1/2的奇异性。由于前文中采用权函数法的表面裂纹应力强度因子的计算公式是通过参考应力强度因子解拟合得到的，而这些参考应力强度因子解同样是采用有限元法计算得到的。在计算这些应力强度因子解时由于采用了虚拟裂纹扩展法，表面点处的应力强度因子实际上是裂纹表面单元的平均值，因此与Franc3D的计算结果有较大差异。

既然FCGPP与Franc3D在计算表面点处的应力强度因子时得出了相差较大的结果，为何两者给出了非常接近的疲劳裂纹扩展寿命。本文认为主要有两个原因，一是为了避免疲劳裂纹在扩展过程中产生不必要的数值噪声，Franc3D采用曲线拟合来获得平滑的裂纹前缘，如图3-5所示。

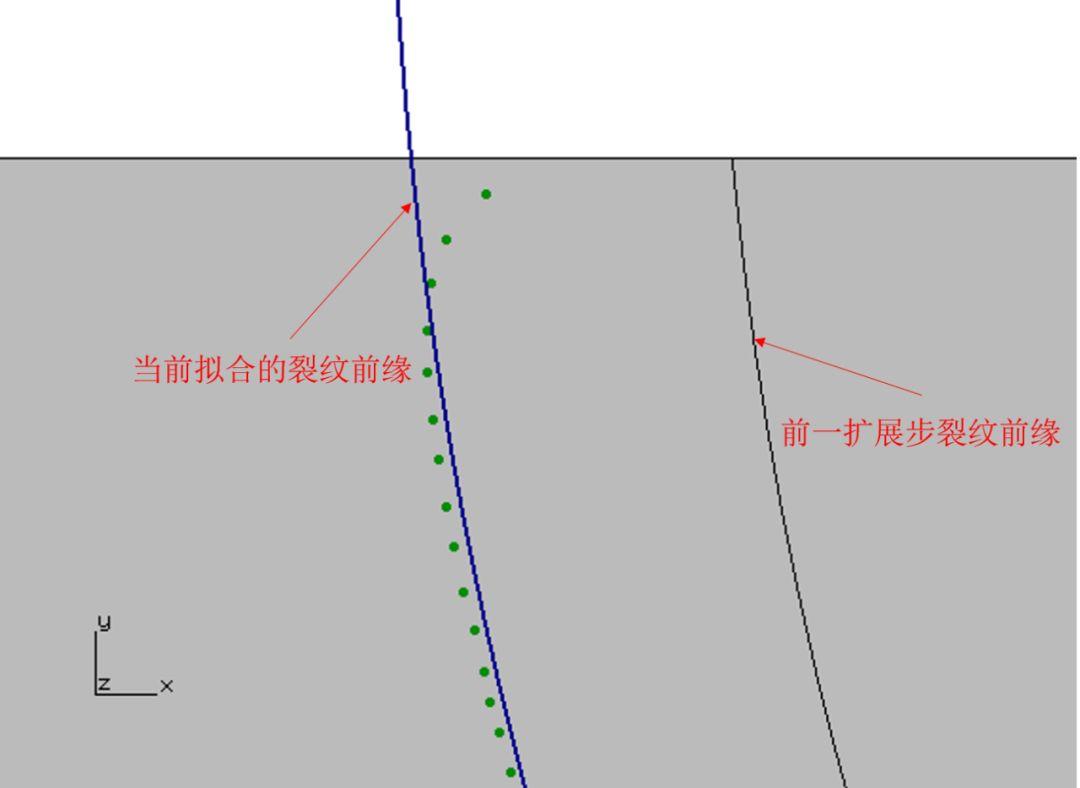
图3-5 Franc3D拟合裂纹前缘轮廓

从图3-5中可以看出，当采用低阶多项式对裂纹前缘进行拟合时，尽管表面点处的应力强度因子下跌会导致疲劳裂纹的扩展增量相对减小，但对最终拟合得到的裂纹前缘影响非常小。这一点从FCGPP与Franc3D计算得到的裂纹形状比a/c的变化也可以体现出来，如图3-6所示。

图3-6 裂纹形状比变化对比

从图3-6中可以看出，FCGPP与Franc3D计算出的表面裂纹形状比变化非常接近，这说明在裂纹扩展的过程中，尽管FCGPP和Franc3D计算得到的裂纹表面点C处的应力强度因子存在较大差异，但在表面点C处的扩展增量几乎是相同的。

此外，Franc3D在计算疲劳裂纹扩展寿命时计算的是通过各个离散裂纹前缘点获得的裂纹扩展寿命的平均值，因此表面点处的裂纹扩展寿命对最终平均化后的扩展寿命影响很小。这两点原因导致FCGPP与Franc3D计算得到的裂纹扩展寿命非常接近。

FCGPP和Franc3D预测的表面裂纹前缘轮廓变化如图3-7所示。

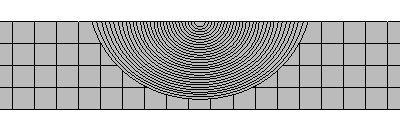
图3-7 表面裂纹前缘轮廓对比

从图3-7中可以看出，由于FCGPP采用简化的两自由度模型进行裂纹扩展预测，因此整个扩展过程中裂纹均为半椭圆形状。Franc3D采用多自由度模型进行预测，得出了更为精确的裂纹前缘轮廓。但这并不影响FCGPP给出了较为精确的表面裂纹扩展寿命。

参考文献

[1] Newman, J. C., Raju, I. S. An empiricalstress-intensity factor equation for the surface crack [J]. Engineering Fracture Mechanics, Vol.15(1), 185-192.

[2] Rice, J. R. Some remarks on elastic crack-tip stress fields [J]. International Journal of Solids and Structures, Vol. 8, 1972, 751-758.

[3] Bueckner, H. F., A novel principle for the computation of stress intensity factors[J]. Zeitschriftf ür Angewandte Mathematik und Mec hanik, Vol. 50, 1970,529-545.

[4] Wang, X., Lambert, S. B., Stress intensity factors for low aspect ratio semi-elliptical surface cracks in finite-thickness plates subjected to non-uniform stresses [J]. Engineering Fractures Mechanics,Vol. 51(4), 1995, 517-532.

[5] Wang, X., Lambert, S. B., Stress intensity factors and weight functions for high aspect ratio semi-elliptical surface cracks in finite-thickness plates [J]. Engineering Fractures Mechanics, Vol.57(1), 1997, 13-24.

[6] Yuan, K. L., Residual stress analysis and fatigue strength assessment of welded joints with ultrasonic impact treatment(UIT) [D]. Yokohama National University, 2015.