如何在ABAQUS中绘制心形曲线
今天是情人节,看到很多人在刷如何绘制心形曲线,作为一名工科生,作者突发奇想,是否能够在ABAQUS中也完成心形曲线的绘制,虽然以前也曾看到过类似的案例,但自己从未尝试过。因此,本文将尝试利用ABAQUS用户子程序,完成心形曲线的绘制。
1. 心形曲线解析表达式
要想完成心形曲线的绘制,首先需要确定一个心形曲线的表达式。作者首先想到的是笛卡尔心形函数,其表达式为:
在极坐标系中可得到如图1.1所示的心形曲线。
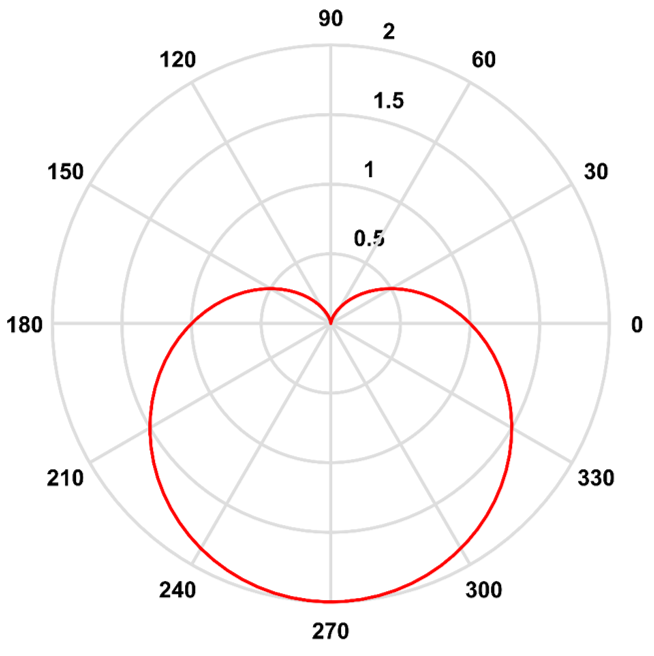
图1.1 笛卡尔心形线
该心形线的θ从0出发到π,完成了图形顶端的心形凹口的绘制,随后从π到2π完成了下半部分图形的绘制。但该曲线并没有很好的反映心形线的特点,原因是曲线的下端没有形成一个尖,这一点从该函数的导数可以看出,在θ=3π/2处的导数为0,这意味着在下端有水平切线。
并且,该心形曲线没有调整的空间,无法通过调整参数来使得心形形状更饱满或底部更尖锐。
为了得出更为完美的心形曲线,且兼具调整性,作者查阅了相关资料1,找到了几个更为完美的表达式:
这些表达式均可得到三维心形图像。由于这些表达式均为三个变量的隐函数,无法直接通过MATLAB的surf函数获得三维曲面,但可以通过isosurface函数间接绘制得到。例如,作者选取第三个表达式进行绘制,在MATLAB中的代码如下所示。
clear,clcx=linspace(-5,5,100);y=linspace(-5,5,100);z=linspace(-5,5,100);[X,Y,Z]=meshgrid(x,y,z); %网格化V=(X.^2+9/4*Y.^2+Z.^2-1).^3-X.^2.*Z.^3-9/80*Y.^2.*Z.^3;%绘制等值面isosurface(X,Y,Z,V,0)axis equal;camlightxlabel('X');ylabel('Y');zlabel('Z');lighting gouraud
绘制得到的三维心形曲面如图1.2所示。该心形曲线是利用MATLAB的isosurface函数计算等值面获得的。在计算中利用linspace函数在x,y,z三个方向上各取了100个计算点,得到了100×100×100的矩阵。增加计算点能够得到更为平滑的曲面,但也会相应地增加计算时长。
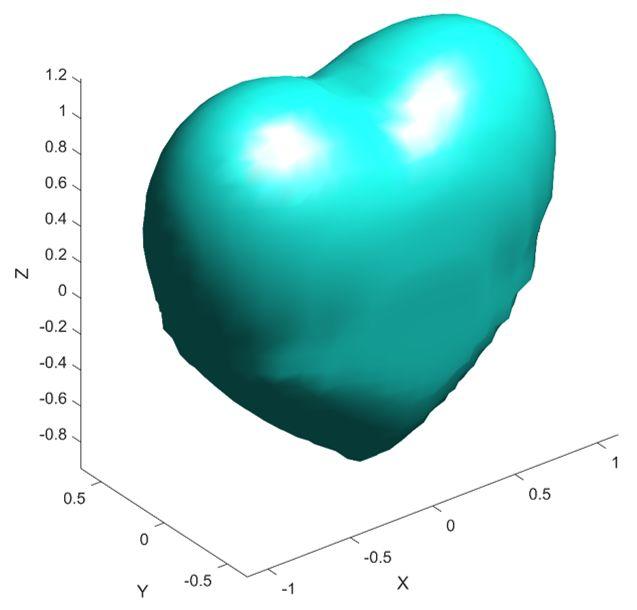
图1.2 三维心形曲面
从图1.2中可以看出,通过在三维心形曲面上取不同位置的截面,即可得到不同形状的二维心形曲线。例如,分别取Z=0和Z=0.4,可得到如图1.3所示的心形曲线。
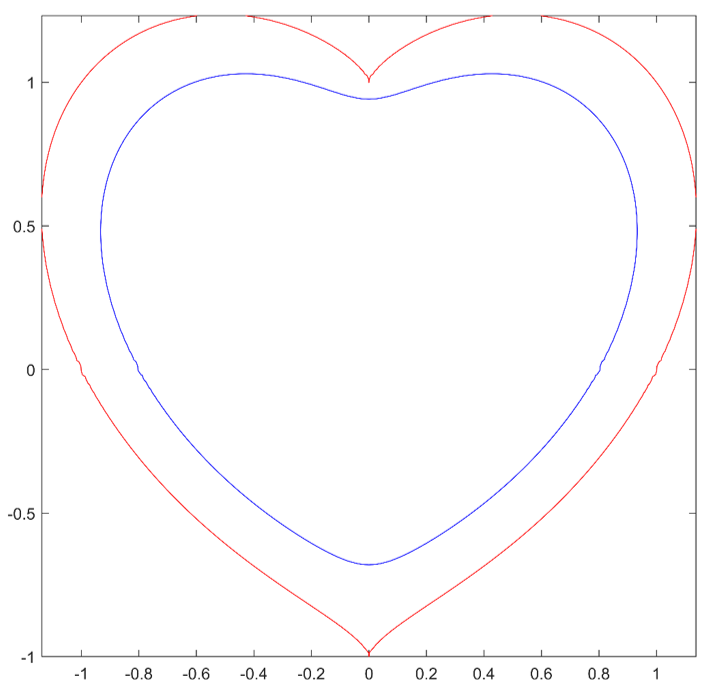
图1.3 二维心形曲线
图1.3中的曲线仍然为隐式表达式,可通过MATLAB的ezplot或fimplicit函数绘制得到,代码如下所示:
figurey=0;p=fimplicit(@(x,z) (x^2+9/4*y^2+z^2-1)^3-x^2*z^3-9/80*y^2*z^3);p.Color='r';hold ony=0.4;p=fimplicit(@(x,z) (x^2+9/4*y^2+z^2-1)^3-x^2*z^3-9/80*y^2*z^3);p.Color='b';axis equal
2. 基于ABAQUS绘制心形曲线
在ABAQUS中绘制心形曲线的基本思路为利用在平板上施加特定的载荷,使得该载荷的分布满足心形曲线的解析表达式,即可得到相应的心形图案。而任意分布载荷的施加,可借助ABAQUS用户子程序来完成。对于载荷类型,可以有多种选择,例如在应力分析中,利用用户子程序DISP在平板上施加位移边界条件,或利用用户子程序DLOAD在平板上施加集中力或压力载荷。也可以在热传导分析中,利用用户子程序DISP指定特定的温度值,或利用用户子程序DFLUX指定热流密度。
为了获得较好的表现效果,作者最终选择了在热传导分析中通过用户子程序DFLUX指定热流密度来完成心形曲线的绘制。这主要是基于以下的考虑:上述的用户子程序只能在单元积分点上被调用,因此心形曲线并不能完全落在单元积分点上。显然,指定一个心形的范围可以获得更好的显示效果,因此,本文将图1.3中两条心形曲线围成的区域作为载荷施加的范围。
需要注意的是,在心形区域的内外边界上仍然将存在不平滑的区域,如图1.4所示。

图1.4 心形区域不平滑边界
尽管加密网格可以获得更好的显示效果,但也会增加计算时长。而在热传导分析中使用热流密度DFLUX进行加载可以很好的避免这个问题,因为随着温度的扩散,心形曲线的边界也会随之趋于平滑。
具体的实现方法如下。首先在XY平面建立一个长宽均为3m的正方形平板(平板尺寸任意,但应能够完全容纳心形区域),平板中心位于坐标原点,如图1.5所示。

图1.5 矩形平板
对于热传导分析,分别指定材料的密度ρ为7790kg/m3,比热容c为470J/(kg∙K),导热系数k为41W∙km-1。在分析步中创建两个瞬态热传导分析步,第一个分析步的计算时间为1s,用于将热流密度载荷施加在平板上;第二个分析步的计算时间取为900s,用于模拟冷却过程中的热传导。
在Load模块中,创建体热流密度载荷,作用区域选择为整个平板,Distribution选择为User-defined,即用户自定义热流密度,如图1.6所示。
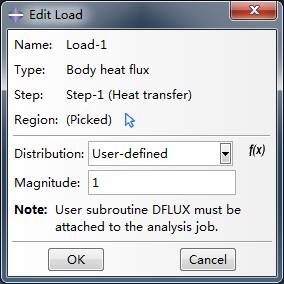
图1.6 定义热流密度
在第二个分析步中,取消激活热流密度载荷,如图1.7所示。

图1.7 取消激活热流密度
在Create Predefined Field中创建初始温度场,并设置初始温度为20ºC。
模型所用的单元尺寸为0.05m,单元类型选择用于热传导分析的DC2D4单元。
分析所用的DFLUX用户子程序的完整代码如下所示。
SUBROUTINE DFLUX(FLUX,SOL,KSTEP,KINC,TIME,NOEL,NPT,COORDS,1 JLTYP,TEMP,PRESS,SNAME)CINCLUDE 'ABA_PARAM.INC'CDIMENSION FLUX(2), TIME(2), COORDS(3)SNAMEC 获取当前积分点坐标X=COORDS(1)Y=COORDS(2)Z=0V1=(X**2+9/4*Z**2+Y**2-1)**3-X**2*Y**3-9/80*Z**2*Y**3!位于曲线外边界内Z=0.4V2=(X**2+9/4*Z**2+Y**2-1)**3-X**2*Y**3-9/80*Z**2*Y**3!位于两曲线封闭区域=TIME(1)*2e8END IFEND IFRETURNEND
程序功能的实现非常简单,首先读取积分点的X和Y坐标,然后判断积分点是否位于两心形线围成的区域内,如果位于心形区域内则计算相应的热流密度。若没有位于心形区域,则热流密度为0。
在计算时需要添加用户子程序,保证计算正常执行,如图1.8所示。
图1.8 添加用户子程序
最终得到冷却过程中不同时刻的心形图案如图1.9所示。
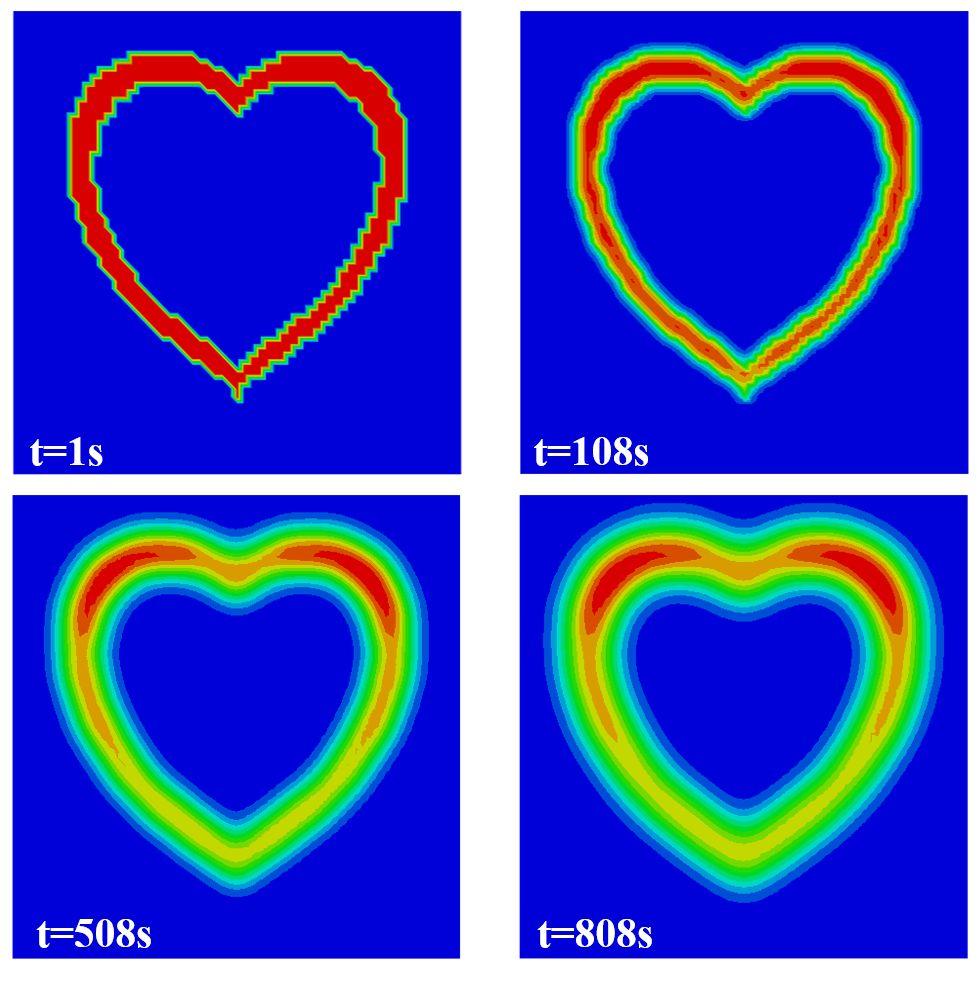
图1.9 不同时刻的心形图案
从图1.9中可以看出,在热传导分析中使用热流密度进行加载能够获得非常好的模拟效果,随着温度的扩散,心形图案的边界趋于平滑。

参考文献
[1] 投畀青赤.如何画心形函数?.逼乎.
https://www.zhihu.com/question/267069065




