基于顺序热力耦合分析的平板焊接数值模拟
本文基于有限元软件ABAQUS的顺序热力耦合分析进行平板焊接过程的数值模拟。顺序热力耦合分析是ABAQUS中常用的热-应力分析类型,这种分析类型适用于应力依赖于温度场,而温度场受应力影响较弱的情况。在分析过程中,需要完成两次分析计算:首先进行热传导分析,获得整个结构的温度分布;随后将计算得到的温度以热载荷的形式施加到结构上,并进行应力分析,获得结构的应力分布。由于应力场和温度场之间互不影响,因此相比于完全耦合的热力分析,顺序热力耦合分析求解更为高效。
1. 平板焊接模型及焊接工艺参数
平板焊接采用的网格模型如图1.1所示。平板的厚度为3mm,长宽均为100mm,由于分析具有对称性,因此计算时采用1/2模型进行计算。为了保证计算精度,一般要求在焊接熔池长度内不能少于四个网格,因此焊缝区域的网格尺寸均小于1mm,而远离焊缝的区域采用逐渐增大的网格进行过渡。

图1.1 平板网格模型
数值模拟选取的焊接工艺参数为:焊接总功率Q=1000W,焊接效率η=0.57,焊接速度v=5mm/s。
2. 焊接材料
本次焊接使用的材料为IN718。在热传导分析中,需要用到的材料参数有:导热系数,比热容,密度;在应力分析中,需要用到的材料参数有:弹性模量,泊松比,平均热膨胀系数(线膨胀系数)和屈服强度。IN718相应的材料数据如图2.1至图2.3所示。

图2.1 IN718导热系数及密度随温度变化曲线
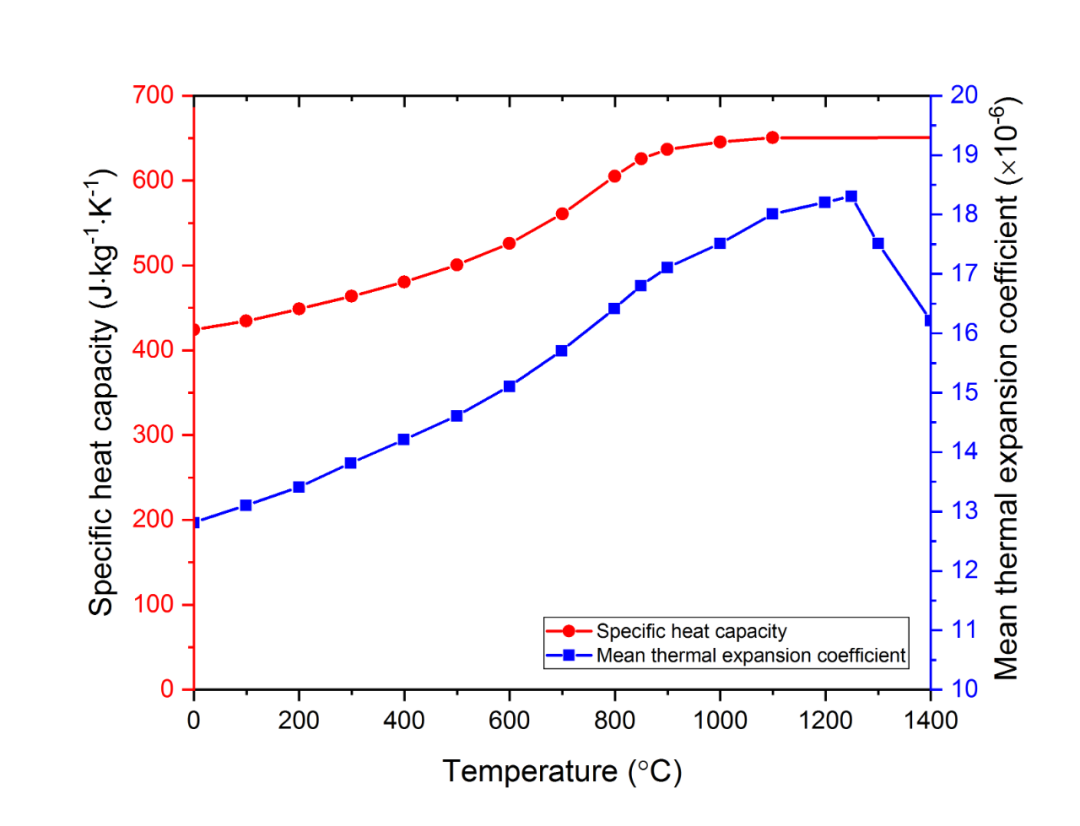
图2.2 IN718比热容及平均热膨胀系数随温度变化
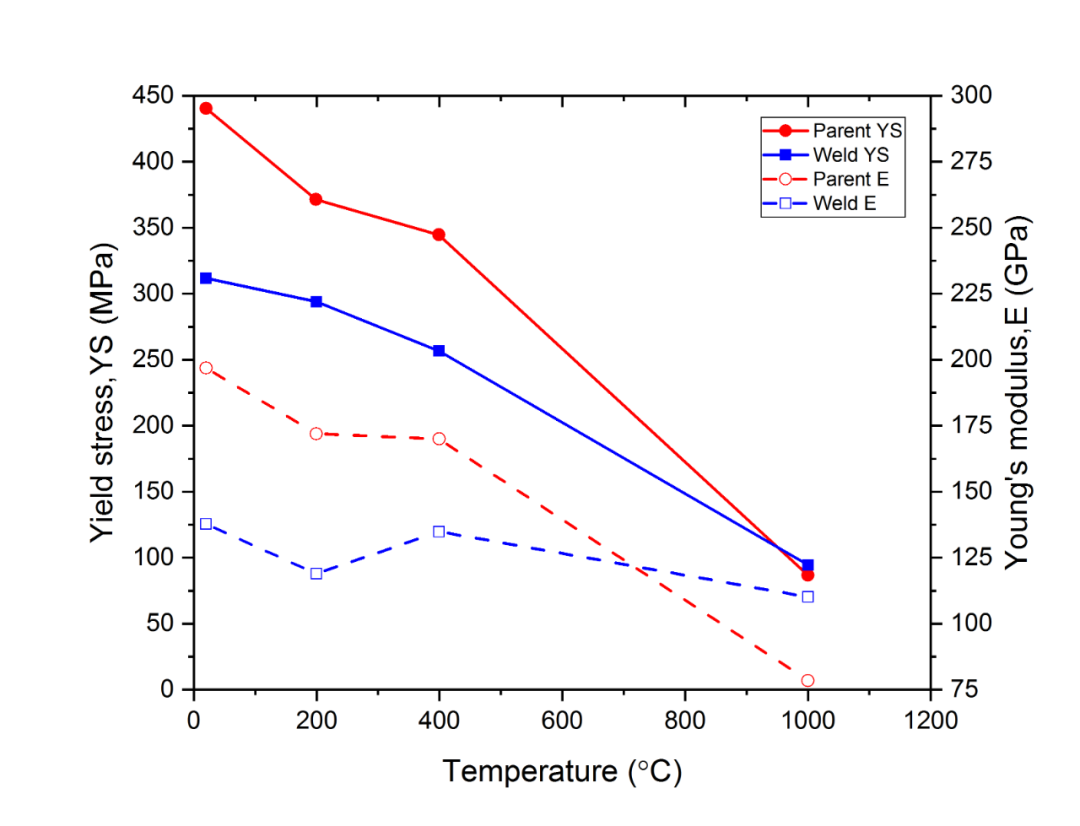
图2.3 IN718杨氏模量及屈服应力随温度变化
图2.3中给出了焊缝和母材对应的杨氏模量及屈服强度,本次计算时均取为母材对应的材料参数。尽管材料的泊松比也会随着温度变化,但将泊松比考虑为依赖于温度的参数会增加计算收敛的难度,因此将IN718的泊松比取为0.3。
3. 焊接热源模型
选取合适的热源模型,对平板焊接残余应力的计算至关重要。焊接热源需要根据焊接类型进行选取,一般常用的焊接热源有双椭球热源、高斯锥形热源、均匀体热源等。为了简化起见,这里本文使用一个圆形面热源进行计算,热源的热流密度分布可表示为:
其中η为焊接效率,Q为焊接总功率,r为圆形热源的半径,这里取为4mm。
在ABAQUS中,上述热源可以通过用户子程序DFLUX施加到有限元模型上。具体的计算原理这里不再赘述,可以参考基于DFLUX的焊接双椭球热源模拟,这里仅给出用到的Fortran程序。
C 程序用于模拟平板焊接热源SUBROUTINE DFLUX(FLUX,SOL,KSTEP,KINC,TIME,NOEL,NPT,COORDS,1 JLTYP,TEMP,PRESS,SNAME)CINCLUDE 'ABA_PARAM.INC'CDIMENSION FLUX(2), TIME(2), COORDS(3)SNAMEC 焊接热源为圆形面热源C 假设焊枪沿X方向的正向移动REAL::PI=3.14159REAL::RADIUS=4E-3 !焊接半径REAL::EFFICIENCY=0.57 !焊接效率REAL::POWER=1000 !焊接功率P=UIREAL::VELOCITY=5E-3 !焊接速度REAL::X_CENTER_INI=-4E-3 !初始时刻热源中心坐标XREAL::Y_CENTER_INI=0 !初始时刻热源中心坐标YC 读取当前积分点坐标X=COORDS(1)Y=COORDS(2)C 计算当前热源中心坐标X_CENTER=X_CENTER_INI+VELOCITY*TIME(2)Y_CENTER=Y_CENTER_INIC 计算热流密度DIST=SQRT((X_CENTER-X)**2+(Y_CENTER-Y)**2)!积分点位于热源范围内=EFFICIENCY*POWER/(PI*RADIUS**2)ELSE=0END IFRETURNEND
需要注意的是,在上面程序中假设焊接热源沿X的正向移动,并且初始时刻焊接热源中心的坐标为(-r,0,0),因此有限元网格也应与程序定义的方向保持一致。
4. 平板焊接温度场计算
将有限元模型导入到ABAQUS中,定义材料IN718,并输入计算需要用到的密度、导热系数及比热容,如图4.1所示。

图4.1 定义材料属性
在Assembly模块中插入平板对应的Part,如图4.2所示。

图4.2 平板有限元模型
注意图4.2中全局坐标的中心与焊接线的起始节点是重合的,并且X正半轴指向焊接热源移动的方向,这样可以保证焊接热源沿平板的中心移动。
在Step模块中定义两个分析步,分析类型为Heat transfer (Transient),第一个分析步的计算时间为21s,由于平板长度为100m,而焊接速度为5mm/s,因此焊接热源完全穿过平板所需的时间约为21s;第二个分析步的计算时间为1000s,用于计算焊接完成后的冷却过程,如图4.3所示。

图4.3 创建热传导分析步
在第一个分析步中设定初始增量为0.1,最大增量为5,最小增量为1E-5,每个增量步允许的最大温升设为500ºC,如图4.4所示。

图4.4 热传导分析步的增量步设置
冷却过程的热传导分析步中取初始增量步为0.001,最大增量为1000,最小增量为1E-5,每个增量步允许的最大温升设为500ºC。
在Interaction模块中创建对流边界条件Surfacefilm condition,对流换热面选择为除对称面以外的所有单元面,如图4.5所示。

图4.5 选择对流换热面
根据牛顿冷却定律,温度高于周围环境的物体向周围媒介传递的热量可表示为:
其中h为对流换热系数,Tbc为周围环境的温度。本次计算中取对流换热系数h为35W∙m-2∙K-1,环境温度取为20ºC,如图4.6所示。

图4.6 设置对流换热边界
除了对流散热,物体还将以辐射的方式向周围介质释放热量,由于在焊接过程中以热辐射的形式释放的能量较少,因此在本文在计算中没有考虑热辐射的影响。在实际计算中,为了提高计算效率,也可以通过调整对流换热系数来考虑热辐射的影响。
在Load模块中创建一个面热流(Surface heat flux),并将面热流作用区域选择为热源作用的区域,如图4.7所示。

图4.7 选择面热流作用区域
需要注意面热流作用区域只需要覆盖热源作用区域即可,尽管选择平板整个表面不会对计算结果产生太大的影响,但由于在所有面热流作用区域的单元积分点上ABAQUS都会调用DFLUX计算热流密度,这显然增加了不必要的计算量。
将面热流密度的分布类型(Distribution)改为User-defined,并将幅值(Magnitude)设为1.
通过Predefined Field定义初始温度场,并将工件初始温度设定为20ºC。
在Mesh模块中,定义整个平板网格的单元类型为8节点线性热传导单元DC3D8。
在Job模块创建热传导分析任务plate_thermal,并指定分析所使用的子程序文件,如图4.8所示。

图4.8 指定子程序文件
图4.9给出了焊接14s时平板表面的温度分布,取IN718材料的熔点为1240ºC,图4.9中灰色 区域即为焊接熔池。

图4.9 平板温度场分布(t=14s)
提取沿焊接方向的热循环曲线,如图4.10所示。

图4.10 焊接热循环曲线
图4.11给出了焊接熔池沿板厚方向的形貌。

图4.11 焊接熔池形貌
从图4.11中可以看出,由于焊接速度过快,因此平板在焊接过程中并没有焊透,并且熔池呈现出扁平的形状,而并非球形。
5. 平板焊接应力场计算
在弹塑性应力分析中,总的应变可以表示为:
其中εije为弹性应变,εijp为塑性应变,εijth为热应变。
热应变εth可表示为:
其中α为材料热膨胀系数,Tref为参考温度。
在顺序热力耦合分析中,通过热传导分析计算得到的温度分布将会施加到应力模型上,从而产生相应的热应变,并最终计算得到对应的焊接应力场。
应力分析使用的模型可以直接通过修改热传导分析模型获得。在模型树中复 制热传导分析模型,并将其更改为plate_mechanic。在Property模块添加应力分析需要使用的材料属性,包括杨氏模量、泊松比、平均热膨胀系数和屈服应力,如图5.1所示。
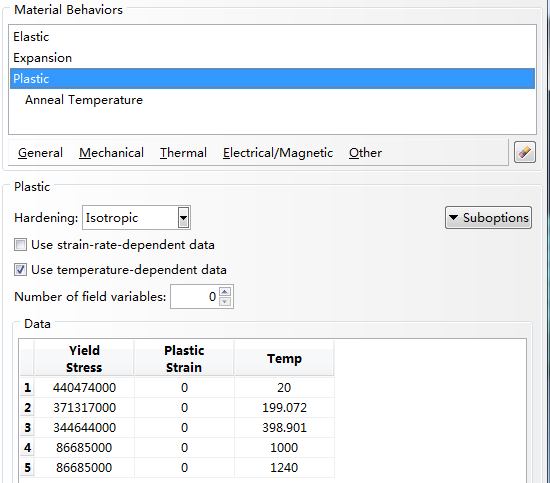
图5.1 定义材料属性(应力分析)
计算时采用的弹塑性本构为等向强化模型,由于前面只给出了IN718的初始屈服应力,没有给出相应的硬化曲线,因此这里假设为理想弹塑性材料。为了考虑材料熔化时的力学行为,在Plastic菜单的Suboptions中选择Anneal Temperature,并将温度值设为1240ºC,即材料的熔点,如图5.2所示。

图5.2 设置材料熔点
当材料点的温度超过Anneal Temperature时,ABAQUS会自动将材料点的等效塑性应变值(PEEQ)设为0,并假设材料为理想弹塑性,只有当温度低于Anneal Temperature才会恢复硬化行为。相应的,在图5.1中需要指定熔点对应的屈服应力值,这里假设与前一个温度数据对应的屈服应力相同。
在Step模块创建两个分析步,分别代表焊接过程和冷却过程,计算时间分别为21s和1000s,与热传导分析设定的时间保持一致,分析类型选择Static, General。打开Nlgeom(大变形开关),设置初始增量步为0.01,最小增量步为1E-5,最大增量步分别为21和1000。
在Interaction模块删除热传导分析创建的对流换热接触。在Load模块中删除热传导分析定义的面热流密度,约束对称面上节点沿Y方向的位移自由度,选择平板端部的节点,并约束X和Z方向的位移自由度,如图5.3所示。

图5.3 边界条件设置
在Predefined Field中创建温度场,选择平板所有节点,将Distribution改为From resultsor output database file,即通过输出数据定义温度场。在File中选择热传导分析计算得到的输出数据库文件(plate_thermal.odb),将Begin step设为1,Begin increment设为0,End step设为1,End increment留空,如图5.4所示。

图5.4 读取焊接过程温度历程数据
图5.4表示在焊接过程对应的分析步(分析步1)中读取热传导分析中焊接过程的温度历程数据。同理,在冷却过程的应力分析中选择热传导分析在冷却过程对应的分析步,如图5.5所示。

图5.5 读取冷却过程温度历程数据
在Mesh模块中更改单元类型为带有减缩积分的8节点线性六面体单元C3D8R。在Job模块创建任务文件plate_mechanic,由于应力分析中并没有调用DFLUX子程序,因此不再需要用到用户子程序文件。
通过应力分析得到工件冷却过后的Von Mises应力分布如图5.6所示。

图5.6 平板Von Mises应力分布(t=1021s)
从图5.6中可以看出,在焊接过后平板出现了翘曲变形,焊接产生的最大残余应力位于焊缝区域,约为440MPa。由于在计算中没有考虑材料的硬化行为,因此计算得到的最大残余应力与图2.3中母材在常温下的屈服应力非常接近。
图5.7给出了焊接过程的等效塑性应变(PEEQ)分布。

图5.7 焊接过程的等效塑性应变(PEEQ)分布(t=14s)
从图中可以看出,在材料属性中设置了Anneal Temperature后,熔池区域的PPEQ值为0,而熔池后方区域由于温度逐渐下降至低于熔点,因此开始累积塑性应变值。
图5.8给出了沿平板中心的残余应力分布。

图5.8 沿平板中心的残余应力分布
从图中可以看出,在焊缝区域,平板所受的纵向应力(S11)远大于横向应力(S22),并且当远离焊缝之后,横向应力出现了明显下降的趋势,这也表明焊接产生的残余应力主要集中在焊缝区域,这主要是由于焊缝区域材料不均匀热变形引起的。
图5.9给出了沿焊接线上的残余应力分布。

图5.9 沿焊接线的应力分布
从图5.9可以看出纵向应力和横向应力在焊接线上表现出了相同的分布趋势,只是应力水平有所不同。并且沿着焊接线的中部区域,出现了应力逐渐上升的趋势。尽管平板是完全对称的,但这里的应力分布却并不是对称的,本文认为这主要是由于在焊接过程中焊件的整体温度逐渐上升,导致最终获得残余应力也出现了逐渐上升的趋势。
参考文献
[1] Tanner, David W. J., Life assessment of welded INCONEL 718 at high temperature[D].University of Nottingham, 2009.





