如何在ABAQUS中计算热应变2
在有限元分析中,结构的残余应力变化通常是利用应变计算得到的,而结构产生的应变一般可以分解为:
其中ε为总应变张量,εe为弹性应变张量,εp为塑性应变张量,εth为热-相变应变张量(thermo-metallurgical tensor),εtp为相变塑性张量(transformation plasticity tensor)。热-相变应变εth可以看作由两部分组成,一部分为材料中各个金属相由于热膨胀产生的热应变,另一部分为材料发生相变时由于体积收缩或膨胀产生的应变。在热应力分析中,热-相变应变通常对于残余应力的形成起着非常大的作用,因此在计算中需要将其考虑在内。
在以往的分析中,材料的热应变通常是通过在ABAQUS中定义随温度变化的平均热膨胀系数来计算的,但这样的方法无法考虑材料由于体积收缩或膨胀产生的应变,因为此时热应变不仅依赖于温度变化,与材料在加热和冷却过程中的温度变化历程也是有关的。本文将基于材料性能计算软件JmatPro计算得到的热膨胀曲线,利用ABAQUS用户子程序UEXPAN完成热应变的计算,并将计算结果与热膨胀曲线进行比较。
1.计算原理
为了便于计算程序的验证,本文将构造单个单元的有限元模型,并在该单元上施加特定的温度变化曲线,用于模拟材料的加热和冷却过程。计算得到的节点温度将以热载荷的形式施加到单个单元的应力分析模型,并通过用户子程序UEXPAN完成热应变的计算。
1.1 温度变化曲线的构造
为了模拟材料的加热过程,本文假设加热过程中材料的温度变化可表示为:
其中θ0为初始温度,θS为稳态温度,t为加热时间,λ为一个反映温升速率的参数。为了保证材料在加热之后完全奥氏体化,假定稳态温度TS为1000ºC,加热时间t取为5s,λ取为-2 s-1。
在冷却过程中,假定材料温度以某一恒定的冷却速率下降,本次计算中取为100ºC/s。通过上述参数计算得到的温度变化曲线如图1.1所示。
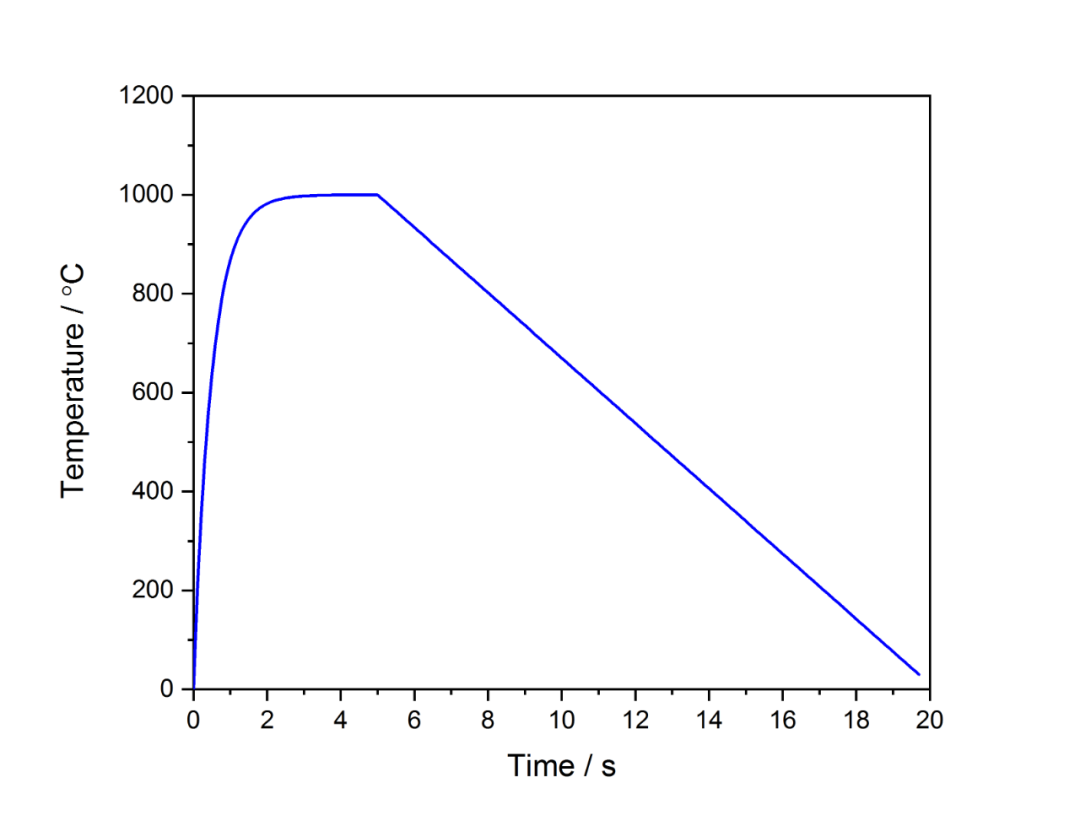
图1.1 温度变化曲线
在热传导分析中,图1.1中的温度变化曲线通过幅值曲线或用户子程序DISP以温度边界的形式施加到整个单元上,用于模拟材料的加热和随后的冷却过程。本文为了便于修改参数,温度变化由子程序DISP计算得到。
1.2 热应变的计算
图1.2为通过材料性能计算软件JmatPro计算得到的SAE3140钢在冷却过程中奥氏体向马氏体转变的热膨胀曲线。
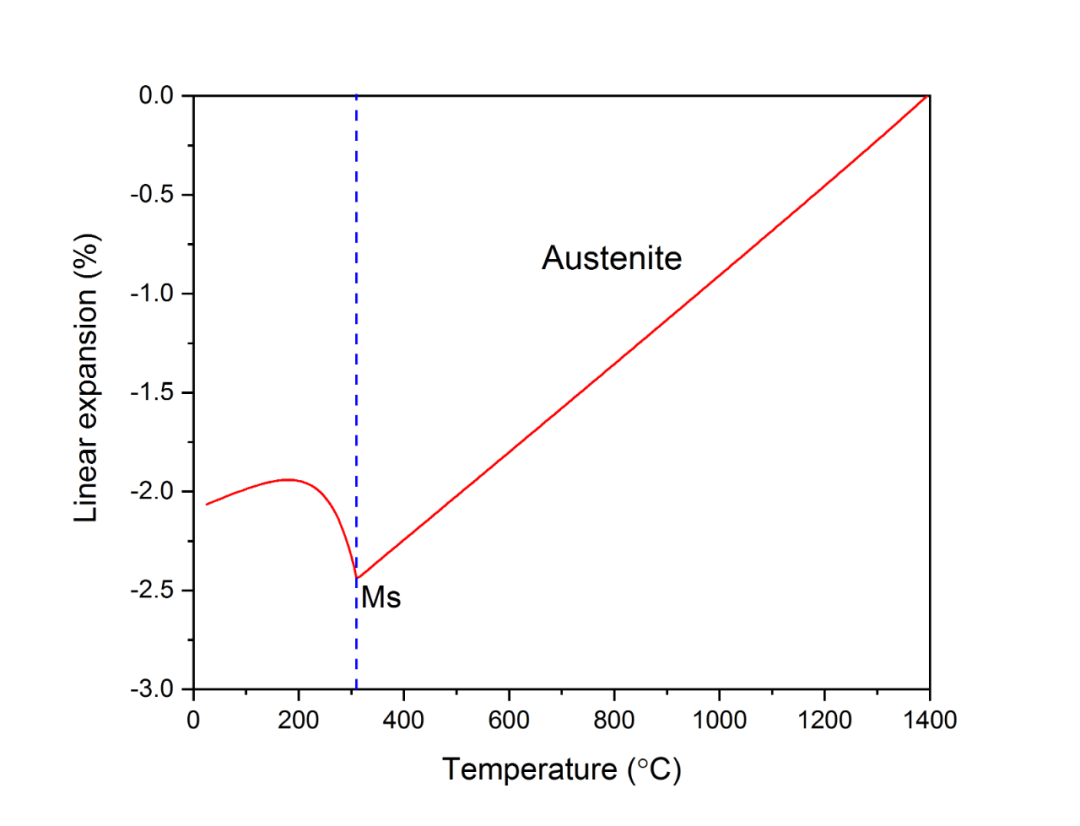
图1.2 SAE3140钢热膨胀曲线
从图1.2中可以看出,在奥氏体向马氏体的转变过程中由于出现了体积膨胀,因此热应变出现了短暂上升的现象。根据前面在如何在ABAQUS中定义热膨胀系数中的分析,如果将马氏体热膨胀曲线和奥氏体热膨胀曲线的交点对应的温度值作为计算平均热膨胀系数的参考温度值,则奥氏体和马氏体的平均热膨胀系数可以近似看作不随温度变化的常数,而奥氏体向马氏体转变过程中的热膨胀系数可根据奥氏体和马氏体的体积分数计算得到。图1.2中的参考温度θ0约为881ºC,确定方法如图1.3所示。
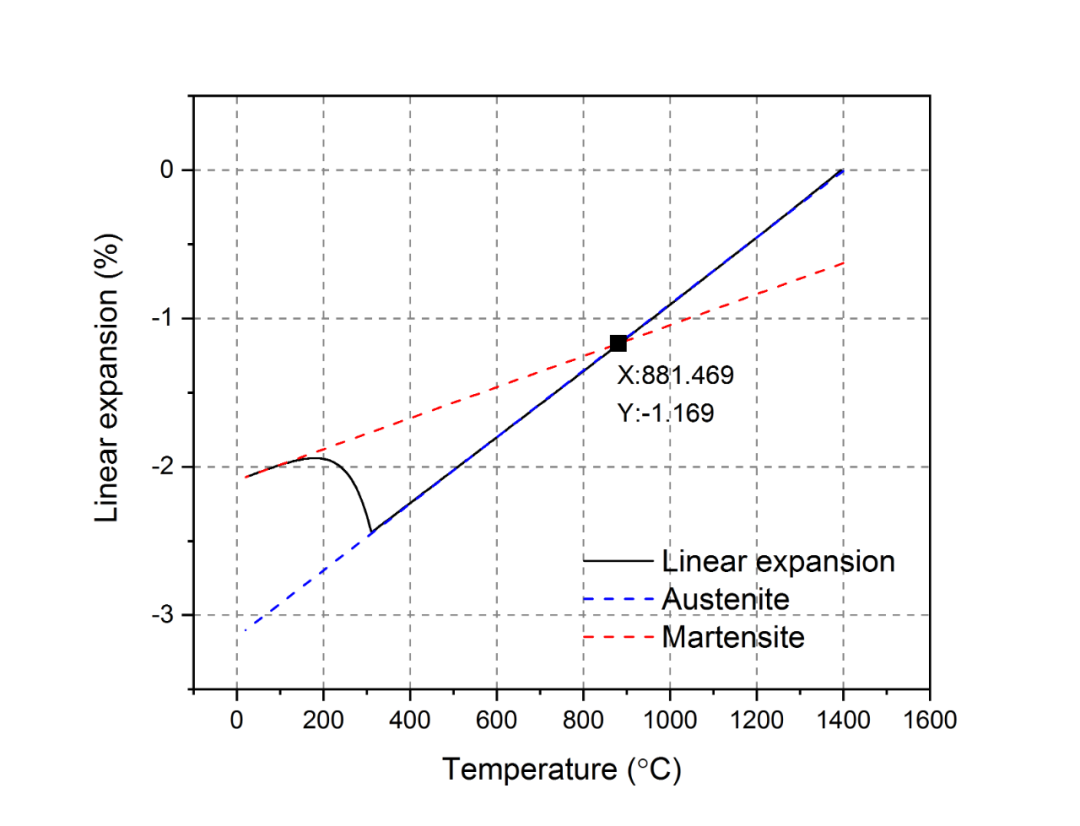
图1.3 参考温度的确定
图1.2中只给出了冷却过程中奥氏体向马氏体转变的热膨胀曲线,对于加热过程,本文假定材料初始相由铁素体和珠光体构成,并假设铁素体和珠光体的平均热膨胀系数与马氏体的平均热膨胀系数相同。根据如何在ABAQUS中定义热膨胀系数中的计算方法,可计算得到各金属相的平均热膨胀系数如表1.1所示。
表1.1 金属相平均热膨胀系数

在加热过程中,铁素体和珠光体将转变为奥氏体,本文采用下述公式来近似计算转变过程中各金属相的体积分数:
当材料温度θ低于A1时:
当材料温度θ高于A3时:
当温度θ满足A1≤θ≤A3时:
其中A1和A3分别为奥氏体转变开始温度和转变终止温度;vp为铁素体和珠光体的体积分数,va为奥氏体体积分数。计算中取A1为722ºC,A3为757ºC。
在冷却过程中,假定奥氏体全部用于马氏体转变。奥氏体向马氏体的转变过程通过Koistinen-Marburger模型计算:
其中,b为与材料有关的常数,Ms为马氏体转变开始温度。计算中取b为0.019ºC-1,Ms为310.5ºC。模型参数的计算方法参见如何在ABAQUS中定义热膨胀系数。
在已知任意温度下各金属相的体积分数后,材料的平均热膨胀系数可通过线性叠加原理计算得到:
则当前温度θ下的热应变为:
其中θI为初始时刻的温度,即热应变为0对应的温度值,本文中取为20ºC。
由于在用户子程序UEXPAN中,热应变是以增量形式进行更新的。因此需要计算当前增量步i相对于前一增量步i-1的热应变增量Δεth:
其中εith和εi-1th分别为增量步i和i-1对应的热应变值。从上式中可以看出,应变增量Δεth与分析的初始温度θI无关,但与参考温度θ0有关。
1.3 计算流程及子程序编写
热应变的计算采用顺序热力耦合分析完成,即首先通过热传导分析完成单元温度场的计算,随后在应力分析中,将节点温度值以载荷的形式施加到模型上,完成热应变的计算。
在热传导分析中,图1.1中的温度变化曲线通过用户子程序DISP以温度边界的形式施加到整个模型上。在应力分析中共使用了三个子程序:SDVINI、USDFLD和UEXPAN。子程序SDVINI用于定义分析初始时刻各金属相体积分数的取值,金属相的体积分数以及体积分数的增量通过状态变量STATEV进行存储,以便在不同的子程序之间完成数据交互。随后各金属相体积分数随温度的变化通过子程序USDFLD进行计算,并将相应的状态变量传递到子程序UEXPAN中。子程序UEXPAN将会根据各金属相的体积分数以及体积分数增量完成热应变增量的计算,整个计算流程如图1.4所示。
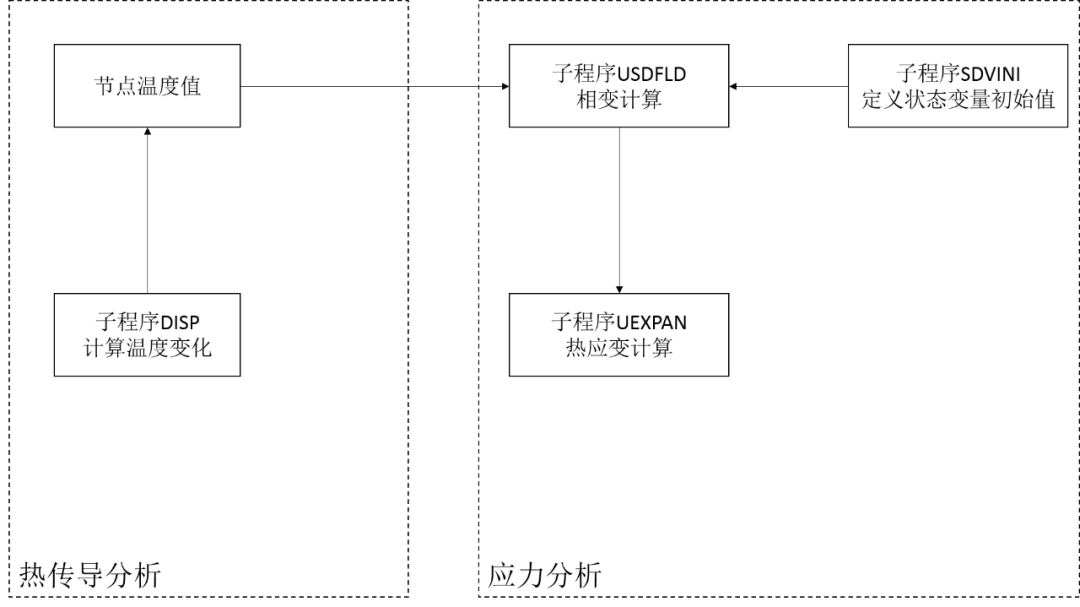
图1.4 热应变计算流程
计算使用的Fortran程序如下所示:
C 程序用于计算相变产生的热应变SUBROUTINE SDVINI(STATEV,COORDS,NSTATV,NCRDS,NOEL,NPT,1 LAYER,KSPT)CINCLUDE 'ABA_PARAM.INC'CDIMENSION STATEV(NSTATV),COORDS(NCRDS)C 注:如果使用GETVRM来访问状态变量STATEV并且分析定义的状态变量超过了15个C 则必须更改ARRAY和JARRAY的维度,使这些数组达到状态变量的最大数目C 为使子程序SDVINI生效C 必须定义关键字*Initional Conditions, Type=SOLUTIONC 程序用于定义状态变量的初始值C STATEV(1)为母材的金属相C STATEV(2)为奥氏体相C STATEV(3)为马氏体相C STATEV(4)为母材金属相的增量(相对于前一增量步)C STATEV(5)为奥氏体相的增量C STATEV(6)为马氏体相的增量C STATEV(1)+STATEV(2)+STATEV(3)=1=1 !假定初始时刻材料全部由母材构成=0=0=0=0=0RETURNENDSUBROUTINE DISP(U,KSTEP,KINC,TIME,NODE,NOEL,JDOF,COORDS)CINCLUDE 'ABA_PARAM.INC'CDIMENSION U(3),TIME(2),COORDS(3)CC 子程序用于定义温度变化C 程序定义了两个分析步C 分析步Heating描述升温过程,分析步Cooling描述冷却过程C 升温过程采用一个指数表达式进行描述,降温过程假定以某一冷却速率匀速下降REAL::TEMP_INI=20 !初始温度REAL::TEMP_STEADY=1000 !加热过程的稳态温度REAL::PARA_LAMBDA=-2 !描述升温速率的参数REAL::COOLING_RATE=100 !冷却速率REAL::TEMP_MAX !加热过程中的最大温度!当前为加热分析步=TEMP_INI+(TEMP_STEADY-TEMP_INI)*(1-!加热阶段的温度变化ELSETEMP_MAX=TEMP_INI+(TEMP_STEADY-TEMP_INI)*(1-!加热阶段上升的最高温度=TEMP_MAX-TIME(1)*COOLING_RATE !冷却阶段的温度变化!温度低于初始温度时终止计算CALL XIT !终止计算END IFEND IFRETURNENDSUBROUTINE USDFLD(FIELD,STATEV,PNEWDT,DIRECT,T,CELENT,&TIME,DTIME,CMNAME,ORNAME,NFIELD,NSTATV,NOEL,NPT,LAYER,&KSPT,KSTEP,KINC,NDI,NSHR,COORD,JMAC,JMATYP,MATLAYO,LACCFLA)CINCLUDE 'ABA_PARAM.INC'CCMNAME,ORNAMEFLGRAY(15)DIMENSION FIELD(NFIELD),STATEV(NSTATV),DIRECT(3,3),&T(3,3),TIME(2)DIMENSION ARRAY(15),JARRAY(15),JMAC(*),JMATYP(*),COORD(*)C 程序用于计算金属相体积分数变化C 为了使子程序USDFLD生效C 必须定义关键字*Initial Conditions, Type=FIELD, VARIABLE=NFIELDC 其中NFIELD为场变量FIELD的数量C VP为母材体积分数,VA为奥氏体体积分数,VM为马氏体体积分数REAL::VP=1REAL::VA=0REAL::VM=0REAL::TEMP_A1=722 !奥氏体化温度A1REAL::TEMP_A3=757 !奥氏体化温度A3REAL::TEMP_MS=310.5 !马氏体转变开始温度MSREAL::PARA_MS_B=0.019 !Koistinen-Marburger模型参数bC 读取前一增量步结束时各金属相体积分数VP=STATEV(1)VA=STATEV(2)VM=STATEV(3)C 获取材料当前的温度值CALL GETVRM('TEMP',ARRAY,JARRAY,FLGRAY,JRCD,JMAC,JMATYP,MATLAYO,&LACCFLA)TEMP=ARRAY(1)C 加热阶段进行奥氏体化计算!当前分析步为加热分析步!加热过程中温度小于A1,材料不会奥氏体化VP=1VA=0VM=0!加热过程温度大于A3,材料完全奥氏体化VP=0VA=1VM=0ELSE !加热过程温度位于A1和A3之间(假定奥氏体体积分数线性增长)VA=(TEMP-TEMP_A1)/(TEMP_A3-TEMP_A1)VP=1-VAVM=0END IFEND IFC 冷却阶段进行马氏体相变计算!当前分析步为冷却分析步!当前温度低于了马氏体转变温度VM=(STATEV(2)+STATEV(3))*(1-&EXP(-1*PARA_MS_B*(TEMP_MS-TEMP)))VA=1-VM-VPEND IFEND IFC 更新状态变量取值=VP-STATEV(1)=VA-STATEV(2)=VM-STATEV(3)IF((KSTEP.EQ.1).AND.(KINC.EQ.1))THEN=0 !修正初始时刻的增量,否则导致热应变计算有误END IF=VP=VA=VMRETURNENDSUBROUTINE UEXPAN(EXPAN,DEXPANDT,TEMP,TIME,DTIME,PREDEF,1 DPRED,STATEV,CMNAME,NSTATV,NOEL)CINCLUDE 'ABA_PARAM.INC'CCMNAMECDIMENSION EXPAN(*),DEXPANDT(*),TEMP(2),TIME(2),PREDEF(*),1 DPRED(*),STATEV(NSTATV)C 程序用于计算相变过程产生的热应变REAL::ALPHA_P=10.46E-6 !母材的平均热膨胀系数REAL::ALPHA_A=22.44E-6 !奥氏体的平均热膨胀系数REAL::ALPHA_M=10.46E-6 !马氏体的平均热膨胀系数REAL::TEMP_INI=20 !初始温度REAL::TEMP_REF=881 !参考温度C 读取金属相的体积分数VP=STATEV(1) !母材体积分数VA=STATEV(2) !奥氏体体积分数VM=STATEV(3) !马氏体体积分数VP_OLD=STATEV(1)-STATEV(4) !上一增量步的母材体积分数VA_OLD=STATEV(2)-STATEV(5) !上一增量步的奥氏体体积分数VM_OLD=STATEV(3)-STATEV(6) !上一增量步的马氏体体积分数C 计算混合相的平均热膨胀系数ALPHA=ALPHA_P*VP+ALPHA_A*VA+ALPHA_M*VM !当前增量步的平均热膨胀系数ALPHA_OLD=ALPHA_P*VP_OLD+ALPHA_A*VA_OLD+ALPHA_M*VM_OLD !上一增量步的平均热膨胀系数C 计算当前增量步对应的热应变值THE=ALPHA*(TEMP(1)-TEMP_REF)-ALPHA_P*(TEMP_INI-TEMP_REF)C 计算前一增量步对应的热应变值THE_OLD=ALPHA_OLD*(TEMP(1)-TEMP(2)-TEMP_REF)-&ALPHA_P*(TEMP_INI-TEMP_REF)C 计算热应变增量=THE-THE_OLDRETURNEND
注意,为了在分析中使用子程序SDVINI和USDFLD,需要定义关键字*Initial Conditions,Type=SOLUTION和*Initial Conditions,Type= FIELD,VARIABLE=N,其中N为场变量FV的数量。由于计算中没有用到FV,因此可以任意定义一个数值。
利用上述程序,可计算得到温度和热应变随时间的变化曲线如图1.5所示。
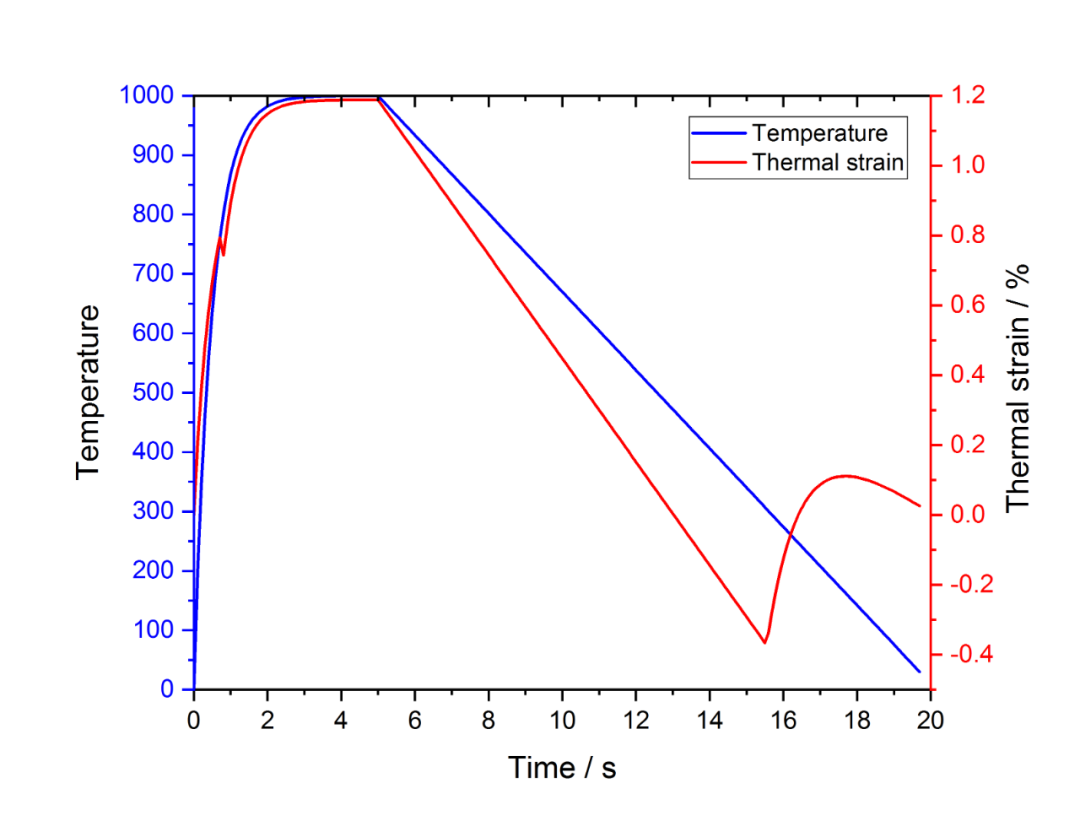
图1.5 温度及热应变随时间变化
从图1.5中可以看出,由于奥氏体化过程中A1温度到A3温度的温度区间非常小,因此从初始相到奥氏体的过程对热应变的影响非常小,而马氏体相变过程中的膨胀效应对热应变影响巨大。
将利用子程序UEXPAN计算得到的热膨胀曲线与通过JMatPro计算得到的曲线进行对比,如图1.6所示。为了获得加热和冷却过程中完成的热膨胀曲线(图1.2只给出了冷却过程),采用JmatPro的Welding Cycle模块进行计算,计算中选择的晶粒度为ASTM 7.5,加热速率为500ºC/s,冷却速率为100ºC/s,在高冷却速率下可保证奥氏体全部转变为马氏体。

图1.6 子程序UEXPAN与JmatPro计算的热膨胀曲线对比
图1.6中,JmatPro计算得到的原始热膨胀曲线在加热过程中起点处的热应变应等于0,为了与子程序UEXPAN的计算结果进行对比,将其下移使得终点处的热应变为0。从图1.6中可以看出,下移后的曲线与UEXPAN计算得到的冷却过程对应的热膨胀曲线基本吻合,这验证计算方法的正确性。而在加热阶段,由于本文假设初始相的平均热膨胀系数与马氏体平均热膨胀系数相同,因此导致计算结果与JmatPro的结果存在误差。当然,如果使用同样的方法,将加热过程中初始相的热膨胀曲线外延至与奥氏体的热膨胀曲线相交,然后利用参考温度来计算初始相的平均热膨胀系数,应该能够取得更好的效果。
结论
本文基于材料性能计算软件JmatPro计算得到的热膨胀曲线,利用ABAQUS用户子程序UEXPAN完成了热应变的计算,计算结果与JmatPro给出的热膨胀曲线比较吻合。本文给出的计算方法能够用于考虑材料相变下的热应变计算。





