利用子程序USDFLD模拟焊缝填充过程

1. 简介

在利用有限元软件ABAQUS进行焊接数值时，焊缝材料的填充过程一般可通过两种方法实现：一种为利用Model Change功能在初始时刻将焊缝单元杀死，随着热源的移动逐步将死单元激活；另一种方法为单元休眠法（Quiet element method），即在初始时刻将材料点的刚度设定为一个较低的水平，随着热源的移动逐渐将其恢复到原有的水平。

两种方法各有其优劣之处，当使用Model Change进行焊缝填充的模拟时，由于可以直接在ABAQUS/CAE中进行操作，因此更为简便和直观。但定义时需要对每一层激活的单元都设定单独的分析步，以及对应的激活时间，当处理的模型规模较大时，模型的前处理过程将变得非常繁琐。尽管在ABAQUS中可以利用Python语言进行二次开发来处理上述过程，但利用Python语言定义Model Change时，每一层焊缝单元只能通过单元号来指定（相比之下，在ANSYS中单元生死法的应用更为简便，可以直接利用APDL语言查询单元的坐标来定义焊缝单元），因此实际应用起来仍有非常大的局限性。单元休眠法需要重新建立焊缝单元的弹塑性本构关系，一般在ABAQUS中需要借助用户子程序UMAT来实现，而子程序UMAT需要开发人员具有比较深厚的理论功底，并且对于较为复杂的本构关系，定义不合理的切向刚度矩阵还将使得ABAQUS分析效率较低，因此实现难度很大。但是，通过子程序可以非常轻易地获取材料点的坐标、温度值等信息，因此使用起来灵活性更强。

实际上，在ABAQUS中还可以通过用户子程序USDFLD来较为简单地实现上述相同的效果，其基本思路为将材料点的特性行为与有限元求解过程中的场变量（Field Value, FV）建立联系，通过控制场变量随时间、坐标和温度等变量的变化来实现材料属性的变化。目前，该子程序在功能梯度材料以及材料损伤、相变的模拟中已经得到广泛应用，国外的很多学者也已经将其应用到焊接数值模拟中的焊缝填充过程。然而目前国内的学者大多使用Model Change进行焊缝填充的模拟，而运用子程序USDFLD进行模拟的案例非常少。本文将以T型接头的焊接为例，尝试利用子程序USDFLD模拟焊缝填充过程，并对运用该方法进行模拟可能存在的问题进行分析。

2. T形接头焊接数值模拟

2.1 T形接头网格模型

计算采用的T形接头的翼板宽度为360mm，长度为210mm，厚度为10mm；腹板的宽度为150mm，厚度为10mm。由于结构具有对称性，因此假设T形接头在焊接时腹板两侧同时施焊，仅建立1/2有限元模型。为了保证计算精度，在焊缝周围的区域采用细密网格进行划分，远离焊缝的区域采用粗糙网格进行过渡，焊缝区域的最小网格尺寸为1.2mm，最终划分得到的有限元网格如图2.1所示。

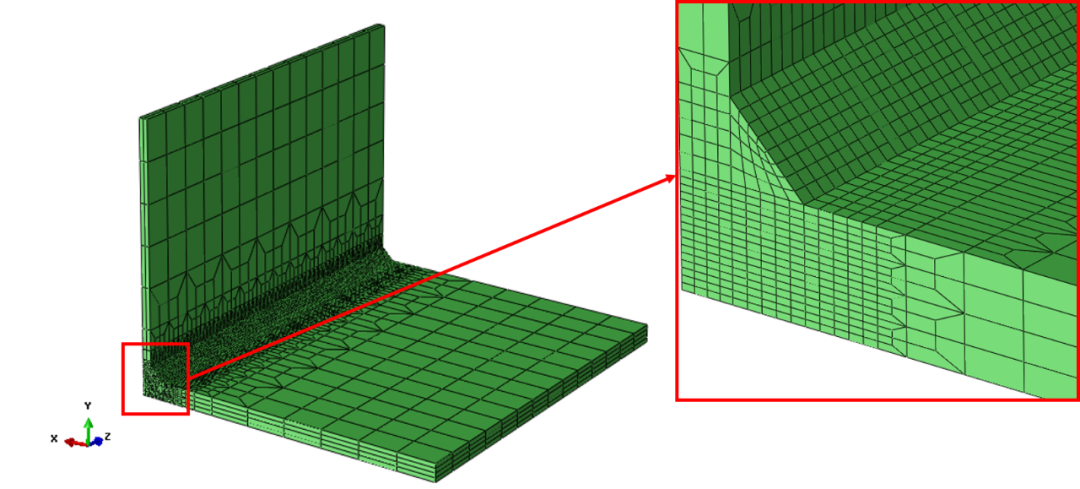
图2.1 T型焊接接头网格模型

在进行T形接头的热传导分析时，在除对称面和焊缝外表面以外的区域施加对流边界条件，对流换热系数取为35W/(m²∙ºC)；在应力分析中，在翼板两角点位置施加固定约束，并约束对称面和腹板两角点处沿X方向的自由度。

2.2 材料模型

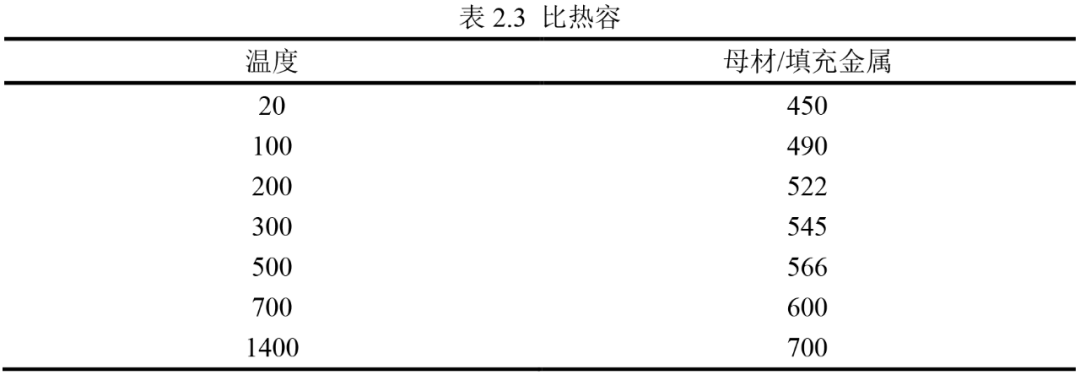
计算采用的材料为SYSWELD材料库中的316L不锈钢，该材料定义有母材和填充金属两种金属相。相关热学属性如表2.1至表2.3所示。

相关力学属性如图2.2至图2.6所示。

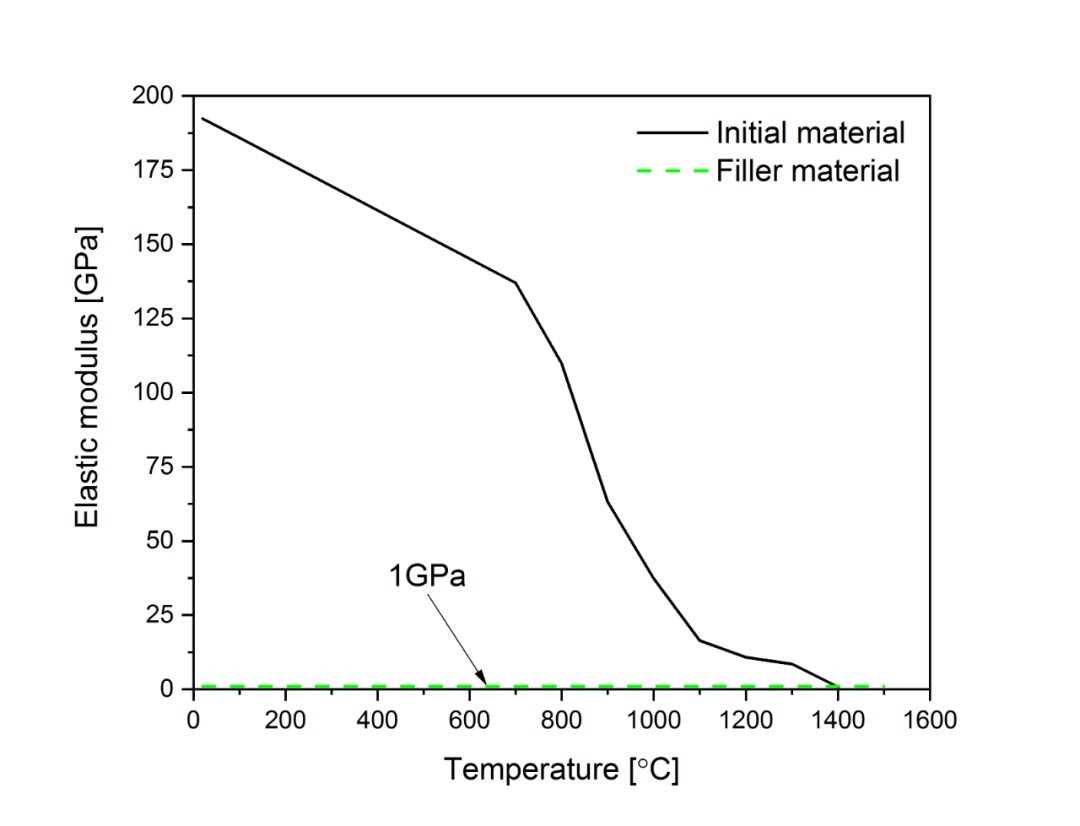
图2.2 弹性模量

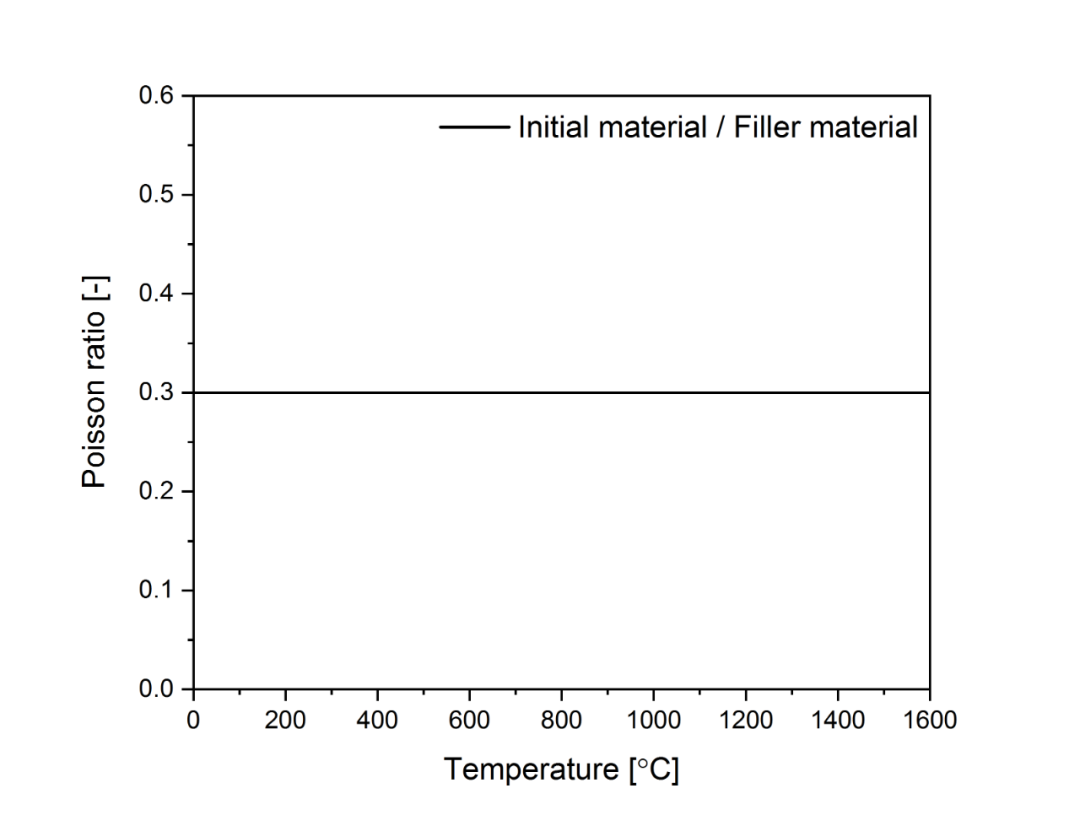
图2.3 泊松比

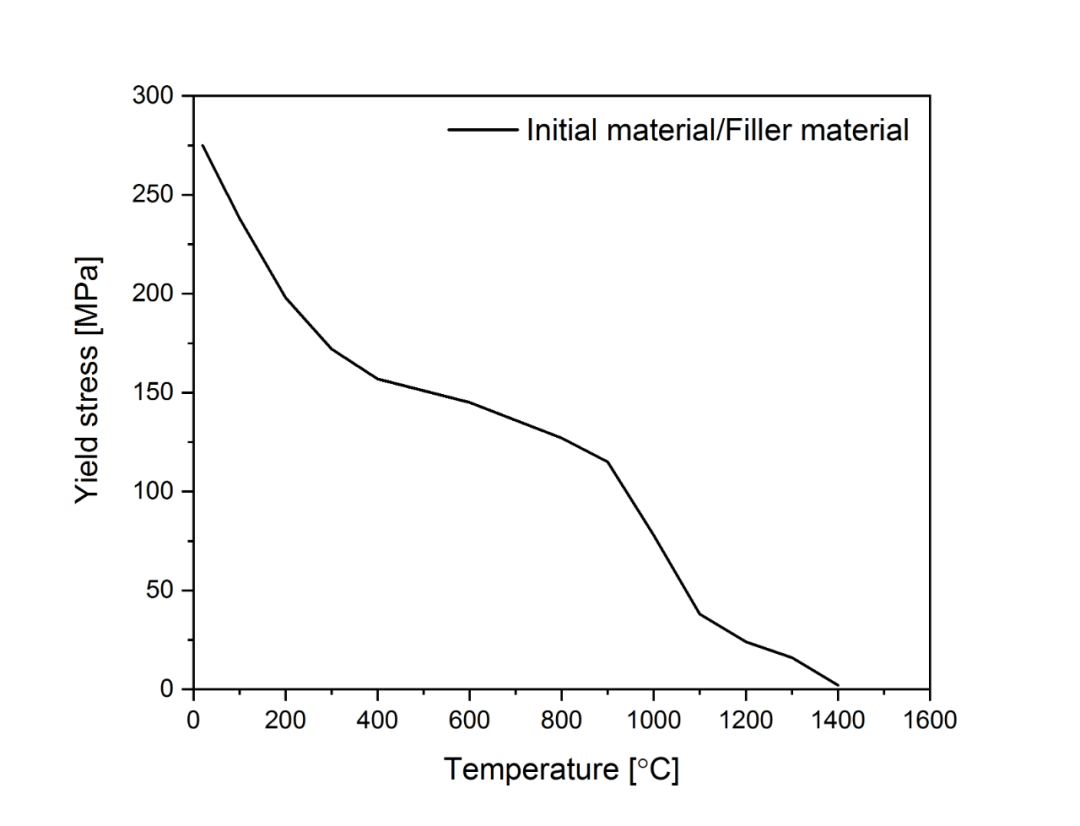
图2.4 屈服应力

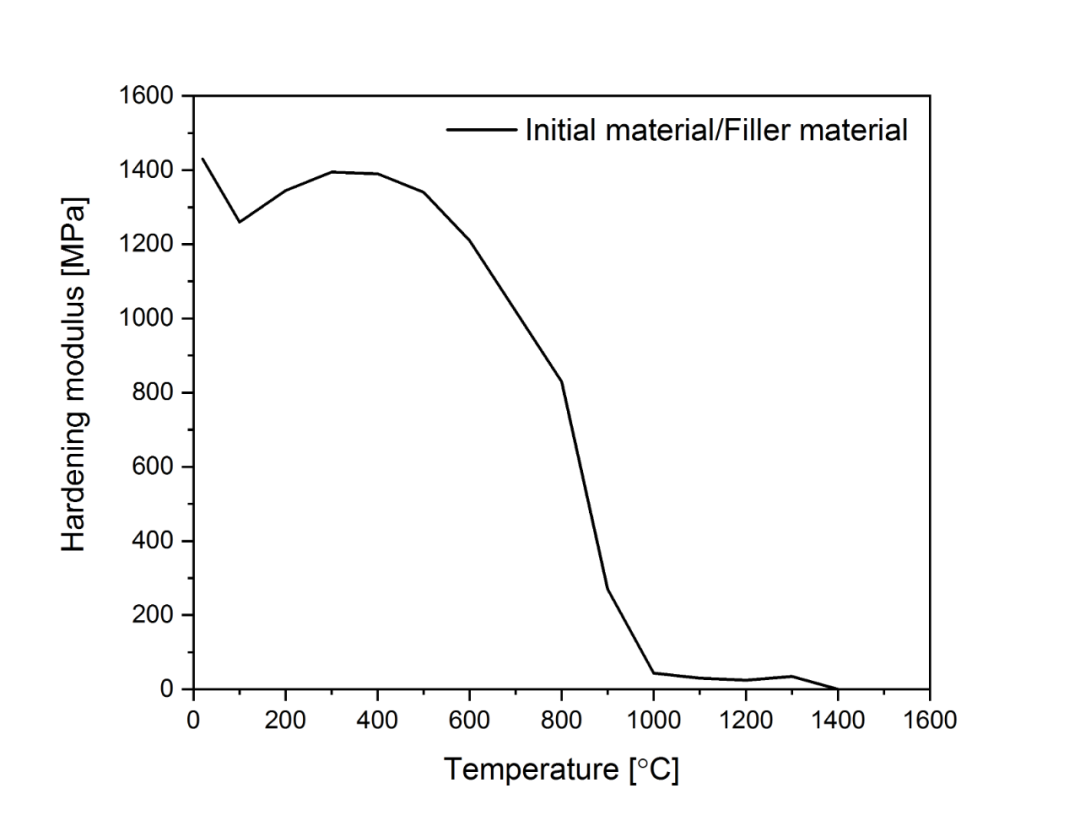
图2.5 硬化模量

图2.6 热应变

2.3 热源模型

由于本文主要探讨焊缝填充过程的模拟，为了简化起见，本文采用均匀体热源来模拟T形接头的焊接过程。均匀体热源假设焊接热量在一定加热体积内是均匀分布的，该热源常用于多道焊接温度场的模拟。在热源作用区域内任意一点的热流密度为：

其中η为焊接效率，U为焊接电压，I为焊接电流，V为热源作用体积。

在确定均匀体热源的热源作用体积V时，可以首先选取整个焊缝体积的1/10到1/5，再利用试验结果进行标定，直到最终获得合适的温度场计算结果。在本次计算中，热源作用段的长度取为5mm，焊缝截面积为25mm²。焊接电压U取为20V，电流I为170A，焊接效率η为0.75，焊接速度v为5mm/s。

2.3 焊缝材料填充原理

焊缝材料的填充是通过用户子程序USDFLD来完成的，假设材料存在两种金属相：母材和填充金属。在ABAQUS中，定义两种金属相的材料属性分别由场变量FV1和FV2控制，则ABAQUS将利用线性混合原理计算当前材料点的材料属性：

上式中，ξ为当前材料的有效材料属性，ξ_i为金属相i的材料属性，FV_i为金属相i在当前材料点的体积分数。定义金属相1为母材，金属相2为填充金属。显然，在分析的初始时刻，对于母材区域的材料有：

对于焊缝区域的材料有：

从图2.2和图2.6可以看出，填充金属的弹性模量被设定为一个非常低的数值（SYSWELD建议不能低于1000MPa），并且热应变为0，这意味填充金属对工件整体刚度的贡献非常小，在热膨胀的过程中也不会产生热应变。通过控制FV1和FV2的取值，可以逐渐将填充金属的弹性模量和热应变恢复到与母材相同的水平，即完成了焊缝的填充过程。

从上面的分析可知，在ABAQUS中利用子程序USDFLD进行焊缝填充模拟时，关键的步骤在于选取恰当的填充策略，用以控制在焊接过程中不同材料点的场变量FV1和FV2的变化。例如，由于填充金属到母材的变化本质上也可以看作是一种相变，因此在本例的316L不锈钢中，SYSWELD同样采用了Leblond模型来计算填充金属到母材的转变，图2.7给出了转变过程中母材的体积分数随温度的变化。

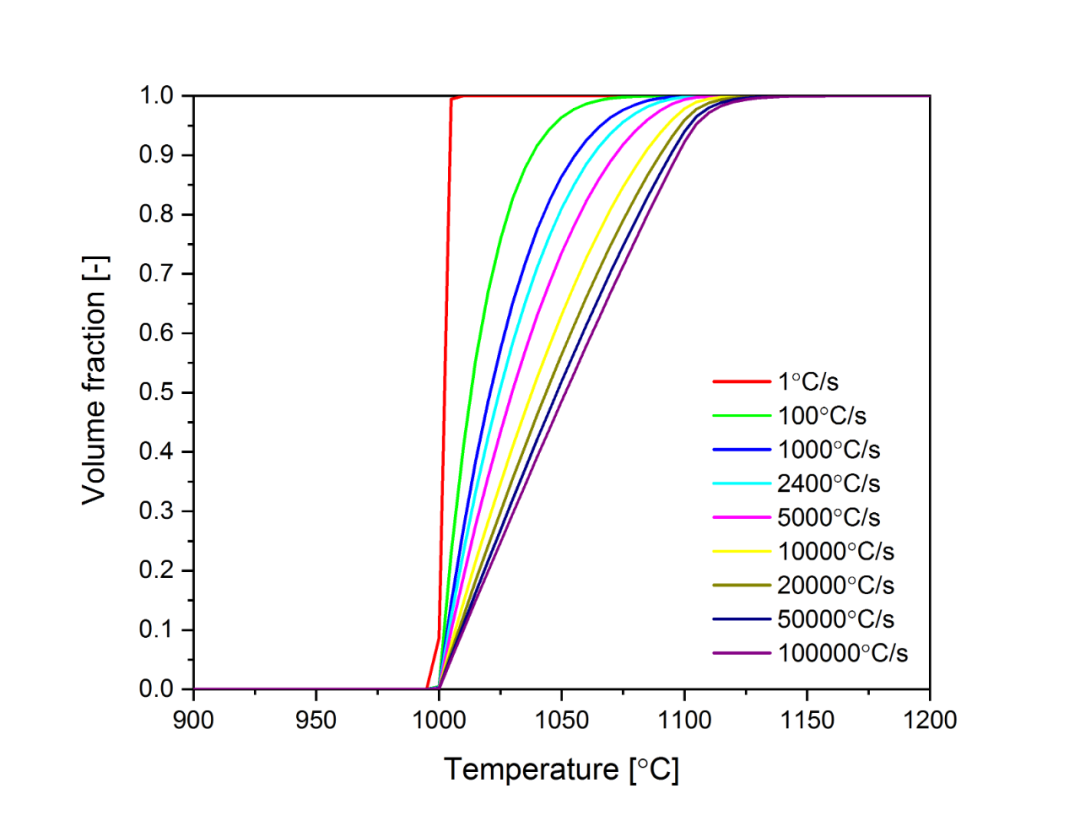
图2.7 填充金属到母材的相变曲线

从图2.7中可以看出，SYSWELD的填充策略为在加热过程，当焊缝区域材料点的温度达到约1000ºC附近时，开始填充金属向母材的转变。该转变将在非常小的一个温度区间内完成，该温度区间取决于材料的加热速率。例如，当材料加热速率为100000ºC/s时，材料点在温度达到1150ºC时完成转变。需要注意的是，当材料点的温度位于该区间之内时，材料将处于两种金属相的混合状态，此时结构的应力值显然是不真实的，因为填充金属相本质上是人为构造的，在实际焊接过程中是并不存在的。只有当填充金属完全转变为母材之后，得到的应力值才是准确的。

除此之外，转变温度的取值也会对计算的收敛性产生影响。由于母材和填充金属的弹性模量在低温区域内差异非常大，如果在较低的温度内开始填充金属向母材的转变，则材料刚度的瞬间变化可能会带来收敛问题。因此，应尽可能地将转变开始温度设定为一个较高的数值，因为此时母材相在高温区域的弹性模量与填充金属相处于相当的水平（参见图2.2）。

实际上，焊缝材料的填充策略并非只能通过判断温度来实现。例如，在ANSYS中，死单元可以通过判断与热源中心之间的距离进行激活；在3D打印之类的增材制造中，也可以通过判断单元号来激活指定的单元；在Simufact.Welding中，只有在冷却过程中当材料点的温度低于指定值（一般设置为熔点）时该单元才会被激活，或者在热源经过该材料点之后的一段时间内（该时间由软件根据焊接速度和熔池大小自动计算）将单元激活，实际上这样的填充策略更接近真实的焊接过程，并且在较高的温度下将单元激活，计算收敛性也会更好。

下面，本文将详细介绍在ABAQUS中利用子程序USDFLD进行焊缝填充模拟的方法，有关用户子程序USDFLD的详细介绍参见ABAQUS用户子程序参考手册:USDFLD。首先，第一个需要解决的问题为如何在子程序USDFLD中判断某一材料点属于母材还是焊缝，以及如何在分析的初始时刻为其FV赋予对应的初始值。对于本文分析的T形焊接接头，由于焊缝截面位于XY平面，比较简单的处理方法为在子程序中查询材料点的坐标，随后根据材料点的坐标范围判断当前材料点是否属于焊缝材料。这样的方法虽然比较直观，但如果焊缝不是规则的几何形状，则实现难度很大。实际上，子程序USDFLD提供了变量CMNAME用于查询用户定义的材料名称，这提示我们可以通过为焊缝和母材定义不同的材料名来进行区分。因此，本文将母材的材料名称定义为BASE_MAT，焊缝的材料名称定义为BEAD_MAT，两种材料的作用区域如图2.8所示。

图2.8 母材和焊缝材料作用区域

图2.8中，绿色 区域的材料名为BASE_MAT，黄色 区域的材料名为BEAD_MAT。需要指出的，两种材料使用的材料属性是完全一致的，这样的处理方式只是为了区分母材和焊缝区域。

在定义两种材料的材料属性时，由于填充材料和母材的密度、比热容、导热系数、硬化曲线相同，因此与普通材料的定义方法完全相同。而弹性模量和热膨胀系数则需要分别指定母材和填充金属相的材料属性，定义方法如图2.9和图2.10所示。

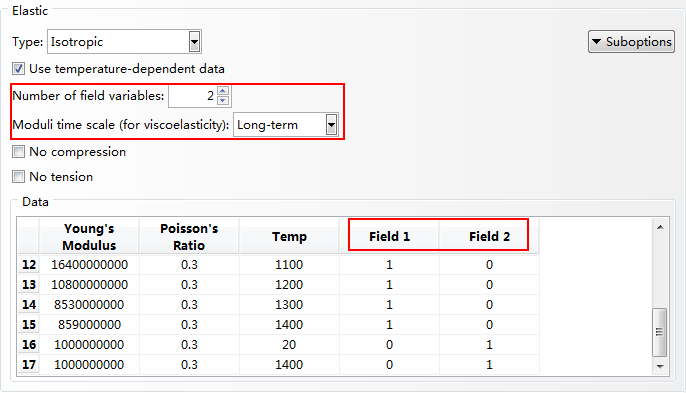
图2.9 弹性模量定义方法

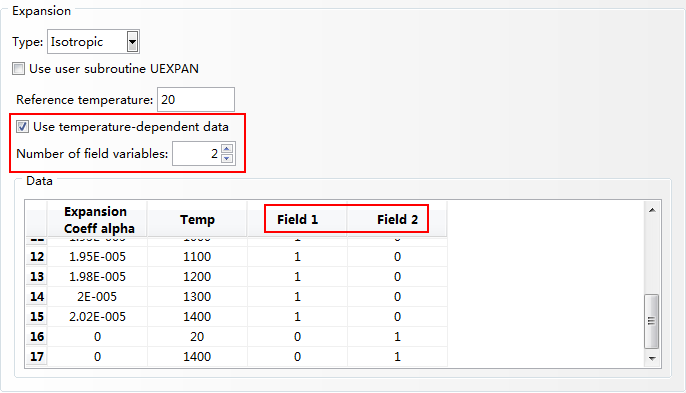
图2.10 热膨胀系数定义方法

如图2.9和图2.10中红色方框所示，由于存在两种金属相，因此Number of field variables的取值为2，其中Field 1表示母材的材料属性，Field 2表示填充材料的材料属性，通过在子程序USDFLD中指定FV1和FV2的取值（母材和填充材料的体积分数），ABAQUS将通过线性混合原理计算有效材料属性。为了使得ABAQUS能够正常调用子程序USDFLD，还需要在材料中定义User Defined Field，如图2.11所示。

图2.11 定义用户自定义场

此外，本文还定义有4个状态变量（STATEV），分别用于存放金属相1体积分数、金属相2体积分数、材料点的加热/冷却速率和前一增量步的温度值，定义方法如图2.12所示。

图2.12 定义状态变量数量

为了在后处理中显示状态变量（STATEV）和自定义场变量（FV）的云图，还需要在场输出中勾选SDV和FV，如图2.13所示。

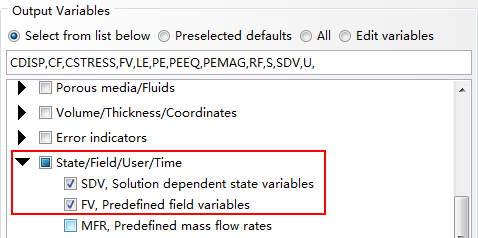
图2.13 输出状态变量和自定义场变量

由于在顺序热力耦合计算的应力分析中，温度场不会包含在应力计算的数据库文件（.odb）中，因此还可以勾选输出节点温度和单元温度值，如图2.14所示。

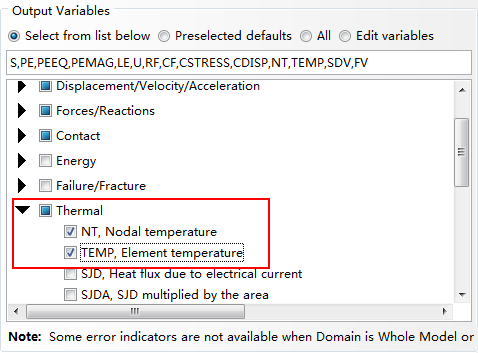
图2.14 输出节点和单元温度

对于ABAQUS 6.14及以下版本，为了正常使用子程序USDFLD，还需要在Model→ Edit keywords→ T_joint_mechnic中定义相应的关键字（T_joint_mechnic为本文使用的应力计算模型，如果需要在温度计算中使用子程序USDFLD，定义方法类似），如图2.15所示。

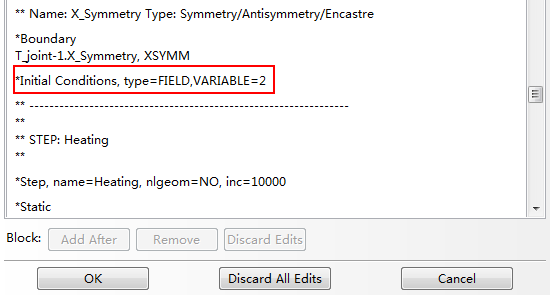
图2.15 子程序USDFLD关键字定义

当用户定义的状态变量比较多的时候，为了便于区分每个状态变量含义，可以在关键字定义中为每个状态变量指定名称，如图2.16所示。

图2.16 指定状态变量名称

在完成相关的前处理工作之后，即可开始子程序文件的编写。子程序文件由两个用户子程序组成，第一个为用于定义热源的DFLUX子程序，关于该子程序的使用方法参见基于DFLUX的焊接双椭球热源模拟，这里不再赘述。第二个子程序即为USDFLD子程序，程序的计算流程如下所述：

（1）首先在分析初始时刻为母材和焊缝赋予对应的FV1和FV2取值。初始时刻可通过分析步号KSTEP和增量步号KINC进行判断，若KSTEP和KINC均为1，即代表第一个分析步的第一个增量步。严格意义上来说，只有增量步号为0才代表计算初始时刻，但当增量步非常小时，这样的处理是合理的。随后，通过材料名CMNAME判断当前材料点属于焊缝区域还是母材区域，对于母材区域，则定义：

对于焊缝区域，则定义：

同时在初始时刻将STATEV(3)和STATEV(4)赋予为0。

上式中，DTIME为当前的时间增量步。

（3）判断当前材料点是否属于填充材料，并且是否处于加热阶段，若同时满足，则利用线性方法计算母材和填充金属相的体积分数：

上式中，T为当前材料点的温度值（TEMP），A₁和A₃分别为转变开始和终止温度。

（4）利用状态变量更新场变量取值，以及温度值：

计算使用的完整子程序如下所示：

C     程序利用单元休眠法(单元软化法)模拟焊缝填充过程      SUBROUTINE DFLUX(FLUX,SOL,KSTEP,KINC,TIME,NOEL,NPT,COORDS,     1 JLTYP,TEMP,PRESS,SNAME)C      INCLUDE 'ABA_PARAM.INC'C      DIMENSION FLUX(2), TIME(2), COORDS(3)      CHARACTER*80 SNAME
C     程序施加移动均匀体热源C     焊接沿Z轴正方向进行
      REAL::EFFICIENCY=0.75     !焊接效率      REAL::WELD_U=20           !焊接电压      REAL::WELD_I=170          !焊接电流      REAL::VELOCITY=5E-3       !焊接速度      REAL::HEAT_L=5E-3        !热源作用长度      REAL::BEAD_AREA=25E-6     !焊缝截面积      C     移动热源计算C     假定焊接初始位置Z=0      Z_INI=-1*(HEAT_L)/2  !焊接起始位置      Z=COORDS(3)       !当前积分点Z坐标      Z_CENTER=Z_INI+VELOCITY*TIME(1)     !热源中心Z坐标      DIST=ABS(Z-Z_CENTER)       !积分点与热源中心坐标的差值            IF(DIST.LT.(HEAT_L/2))THEN   !积分点位于热源作用区域          FLUX(1)=EFFICIENCY*WELD_U*WELD_I/(HEAT_L*BEAD_AREA)      ELSE          FLUX(1)=0      END IF      
      RETURN      END
                  SUBROUTINE USDFLD(FIELD,STATEV,PNEWDT,DIRECT,T,CELENT,     1 TIME,DTIME,CMNAME,ORNAME,NFIELD,NSTATV,NOEL,NPT,LAYER,     2 KSPT,KSTEP,KINC,NDI,NSHR,COORD,JMAC,JMATYP,MATLAYO,LACCFLA)C      INCLUDE 'ABA_PARAM.INC'C      CHARACTER*80 CMNAME,ORNAME      CHARACTER*3  FLGRAY(15)      DIMENSION FIELD(NFIELD),STATEV(NSTATV),DIRECT(3,3),     1 T(3,3),TIME(2)      DIMENSION ARRAY(15),JARRAY(15),JMAC(*),JMATYP(*),COORD(*)      
C     定义相变参数C     当温度低于TEMP_A1时填充材料不发生转变C     当温度高于TEMP_A3时填充材料完全转变为母材,完成填充过程C     当温度位于TEMP_A1和TEMP_A3时采用线性插值计算填充材料体积分数      REAL::TEMP_A1=1100      REAL::TEMP_A3=1200

C     分析初始时刻(分析步号为1,增量步号为1)赋予状态变量初值C     STATEV(1)代表母材的体积分数C     STATEV(2)代表填充材料的体积分数C     STATEV(1)+STATEV(2)==1C     STATEV(3)代表材料点的加热/冷却速率C     STATEV(4)用于存放上一增量步的温度值      IF((KSTEP.EQ.1).AND.(KINC.EQ.1))THEN               IF(CMNAME.EQ.'BASE_MAT')THEN    !判断当前材料点是否属于母材              STATEV(1)=1           !母材的体积分数为1              STATEV(2)=0          ELSE              STATEV(1)=0           !填充材料的体积分数为1              STATEV(2)=1          END IF          STATEV(3)=0    !分析初始时刻设定加热速率为0          STATEV(4)=0    !分析初始时刻设定前一增量步温度值为0      END IF          
C     采用线性模型进行相变计算C     读取当前材料点的温度值            CALL GETVRM('TEMP',ARRAY,JARRAY,FLGRAY,JRCD,JMAC,JMATYP,MATLAYO,     &LACCFLA)      TEMP=ARRAY(1)C     根据温度增量计算加热/冷却速率      STATEV(3)=(TEMP-STATEV(4))/DTIMEC     计算金属相体积分数      IF(CMNAME.EQ.'BEAD_MAT')THEN    !判断当前材料点是否属于填充材料          IF(STATEV(3).GE.0)THEN      !判断当前是否处于升温阶段              IF(TEMP.LT.TEMP_A1)THEN                  STATEV(1)=0                  STATEV(2)=1       !温度低于A1,不发生转变              ELSEIF(TEMP.GT.TEMP_A3)THEN                  STATEV(1)=1                  STATEV(2)=0       !温度高于A3,填充金属转变为母材              ELSE                  STATEV(1)=(TEMP-TEMP_A1)/(TEMP_A3-TEMP_A1)                   STATEV(2)=1-STATEV(1)    !温度位于A1和A3之间,通过线性插值计算              END IF          END IF      END IF
C     更新场变量取值C     FIELD(1)代表母材的材料属性C     FIELD(2)代表填充金属的材料属性      FIELD(1)=STATEV(1)      FIELD(2)=STATEV(2)
C     更新温度值      STATEV(4)=TEMP            RETURN      END

这里，本文仅介绍了焊缝填充过程的模拟的相关细节，关于在ABAQUS中进行焊接模拟的相关操作步骤，参见基于顺序热力耦合分析的平板焊接数值模拟。

3.结果分析

3.1 焊接温度场及金属相体积分数分布

图3.1给出了焊接34s之后T形接头的温度场，图3.2为此时对应的熔池形貌。

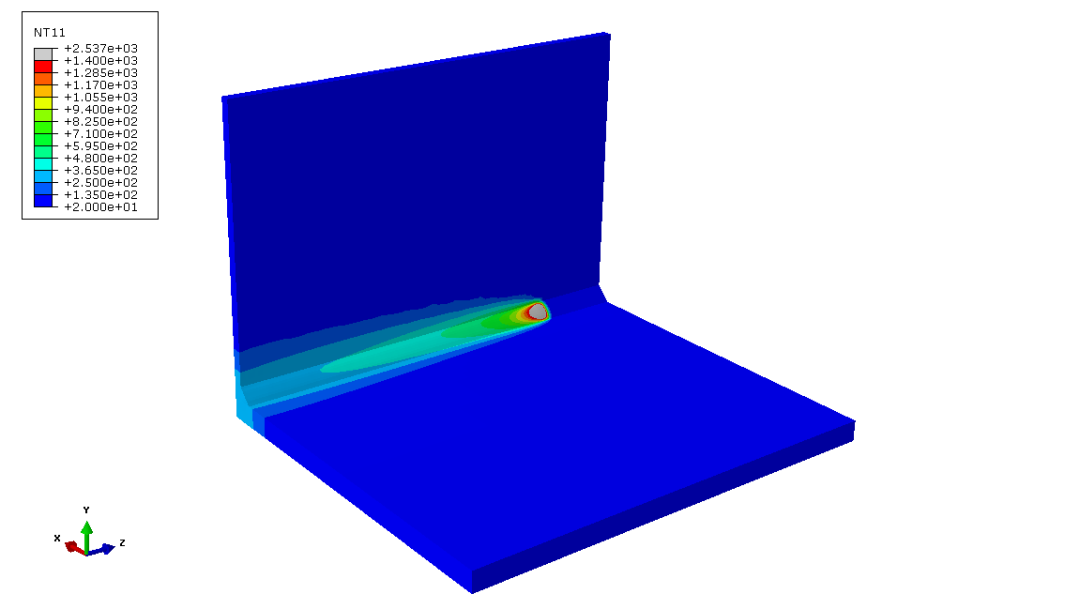
图3.1 焊接温度场分布（t=34s）

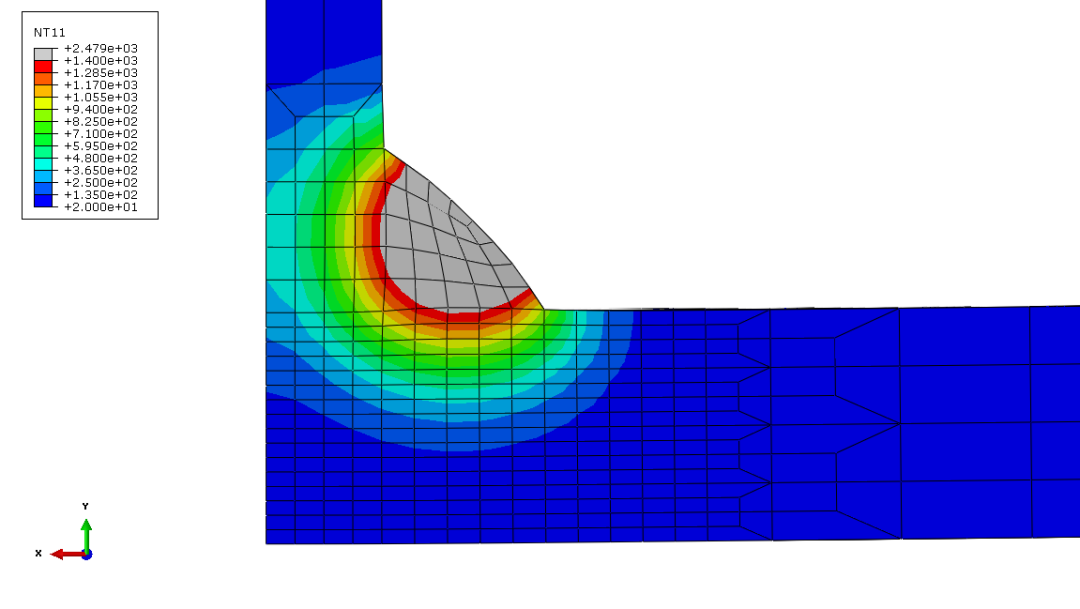
图3.2 焊缝熔池形貌（t=34s）

从图3.2中可以看出，若取熔点为1400ºC，则熔池基本可以覆盖整个焊缝截面。由于本文采用了基于温度的填充策略，因此焊缝区域的温度对填充效果有很大的影响。如果A₁和A₃温度设置过高，则有可能导致焊缝单元的填充金属相无法全部转变为母材；而A₁和A₃温度如果过低，则存在收敛问题。

图3.3给出了当A₁取为1200ºC，A₃取为1300ºC时母材相的体积分数分布，从图中可以看出，在该转变温度下，基本可以保证焊缝区域的填充金属相全部转变为母材相。

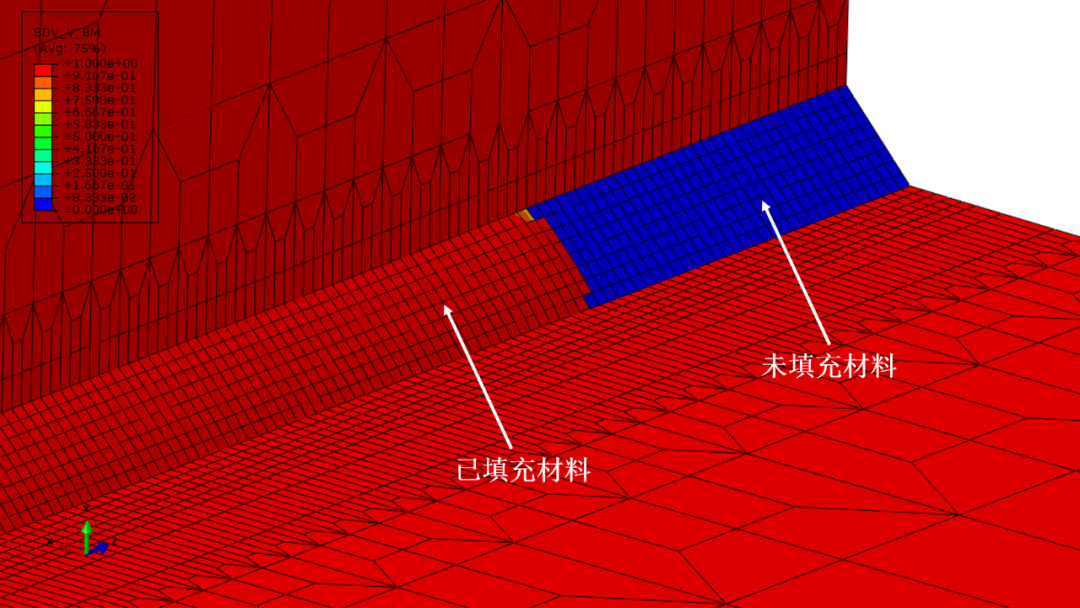
图3.3 母材相的体积分数分布

通过在后处理中输出状态变量不仅可以显示各金属相体积分数的分布，还可以直观地展示焊缝的填充过程。例如，在Field Output的StatusVariable中勾选Use status variable，选择SDV_V_BM(STATEV(1))，并在Remove elements中将Max设定为0.99，如图3.4所示，可得到焊缝材料的填充过程如下所示。

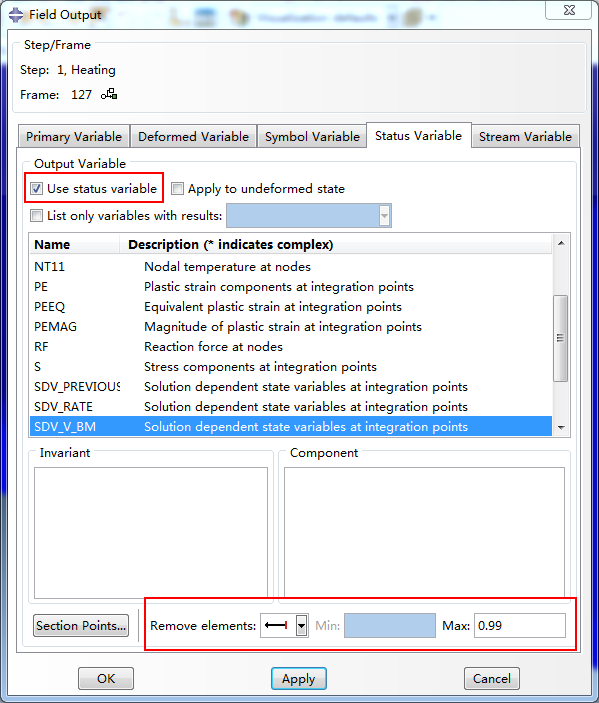
图3.4 后处理显示焊缝填充

从动画中可以看出，由于在焊接初始时刻材料的温度未达到转变温度，因此焊缝起始区域边缘的部分材料没有被正常填充，这显然会对焊接之后的应力分布产生影响。

3.2 焊接应力场分布

图3.5给出了焊接过程中的Von Mises应力分布。

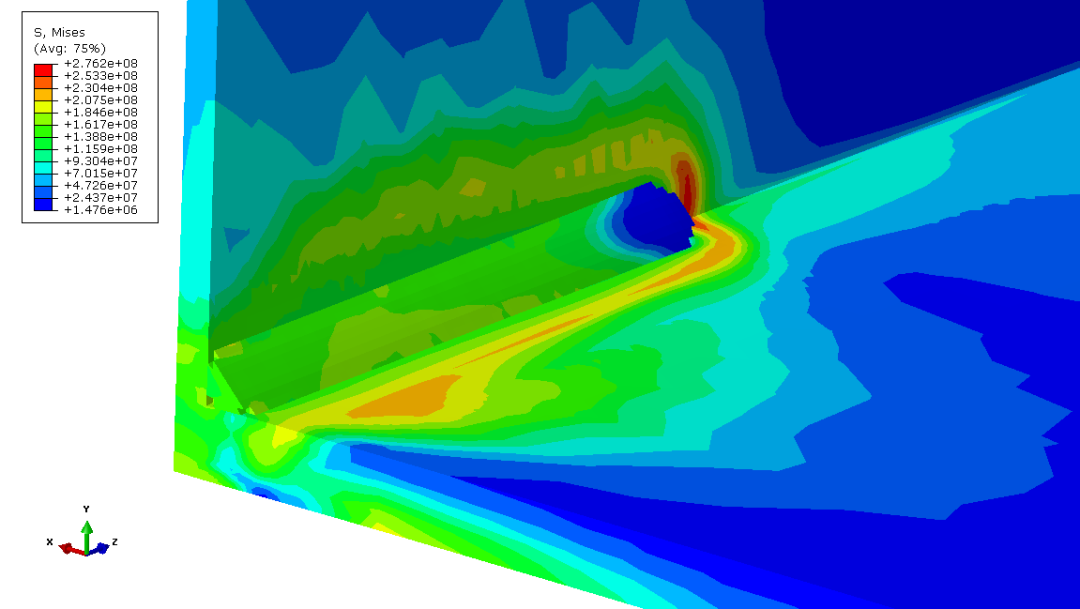
图3.5 焊接过程中的Von Mises应力分布（t=18s）

从图3.5中可以看出，由于在温度场计算中填充材料和母材使用了相同的材料属性，因此实际上在焊接的温度场计算中是没有使用单元填充的。由于焊接过程中的应力分布是由施加在节点的温度载荷引起的，因此焊缝填充对单元应力分布的影响应该很小，大部分残余应力应该是由冷却之后残留的塑性应变引起的。图3.6给出了与图3.5中焊接时间对应的等效塑性应变分布。

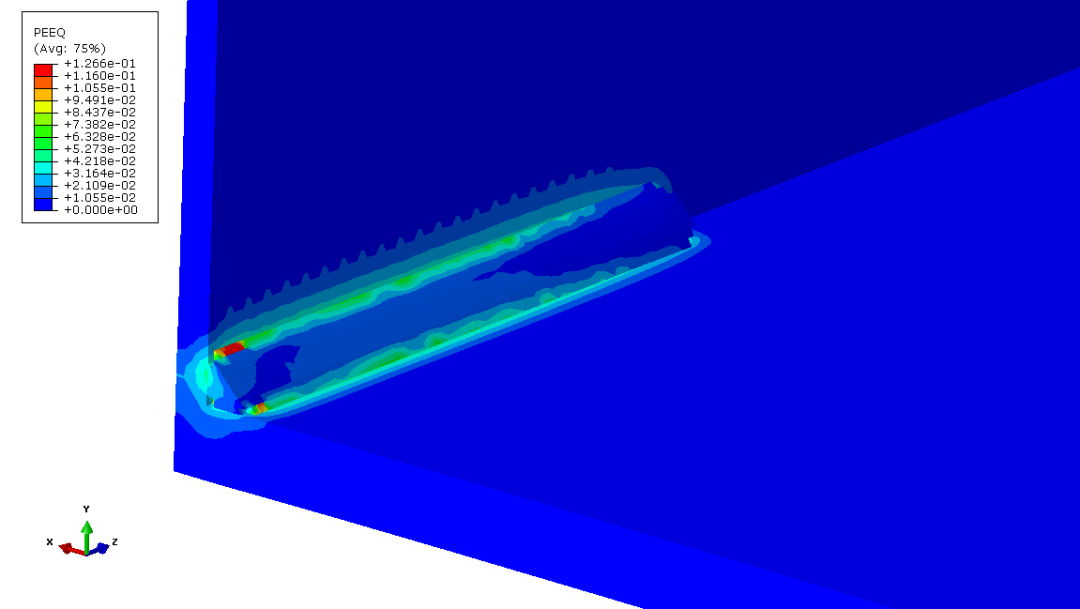
图3.6 焊接过程中的等效塑性应变分布

从图3.6中可以明显看出，由于焊缝起始区域的单元未被正常填充，因此该区域在冷却过程中产生了很大的塑性应变值，从数值模拟的角度来看，这样的情况显然不应该出现。

3.3 填充策略对应力分布的影响

由于转变温度A1和A3对填充效果有非常大的影响，如果转变温度过高，而材料点无法达到对应的温度值，则材料无法 正常填充；若转变温度过低，填充金属相和母材相之间刚度的巨大差异又将使得计算收敛困难。为了探究填充策略对残余应力分布的影响，本文分别选取不同的转变温度进行焊缝填充过程的数值模拟，每种填充策略的转变温度如表3.1所示。

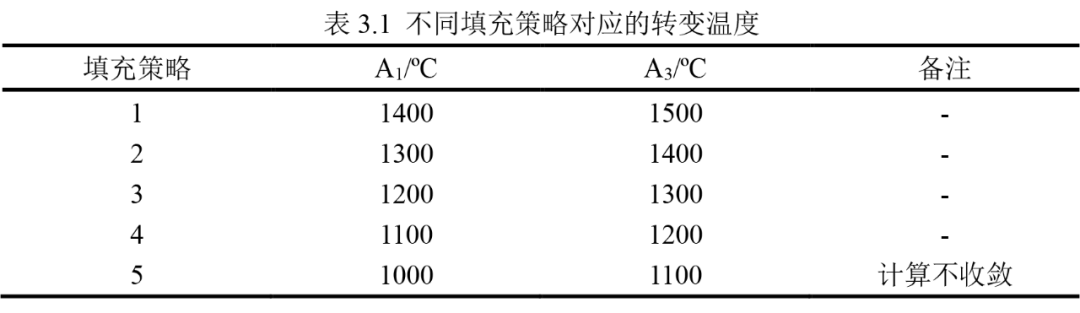
在填充策略5中，当A₃温度低于1100ºC时，ABAQUS在5次迭代之后不收敛，自动终止计算。图3.7给出了由策略1和策略2计算得到焊缝填充完成之后的填充金属相体积分数分布。

图3.7 不同填充策略中填充金属相体积分数

从图3.7中可以看出，由于填充策略1中转变温度过高（转变温度为熔点，从图3.2中的熔池形貌也可以看出熔池未覆盖整个焊缝区域），导致焊缝边缘的填充材料没有完全转变为母材相，而在填充策略2中则没有出现这种情况，当转变温度低于填充策略2中设定的转变温度后，显然这种情况也不会发生。

图3.8给出了在填充策略1下获得的焊接完成之后的Von Mises应力分布。

图3.8 焊接完成之后的Von Mises应力分布（填充策略1）

从图3.8中可以看出，由于焊缝边缘的部分材料点仍处于母材相和填充金属相的混合状态，这导致焊缝边缘的Von Mises应力云图出现了被污染的状况，在这些区域将无法得到正确的应力值。

为了对比不同填充策略对应力分布的影响，本文分别提取了不同策略下沿焊接方向的横向应力分布，如图3.9所示。

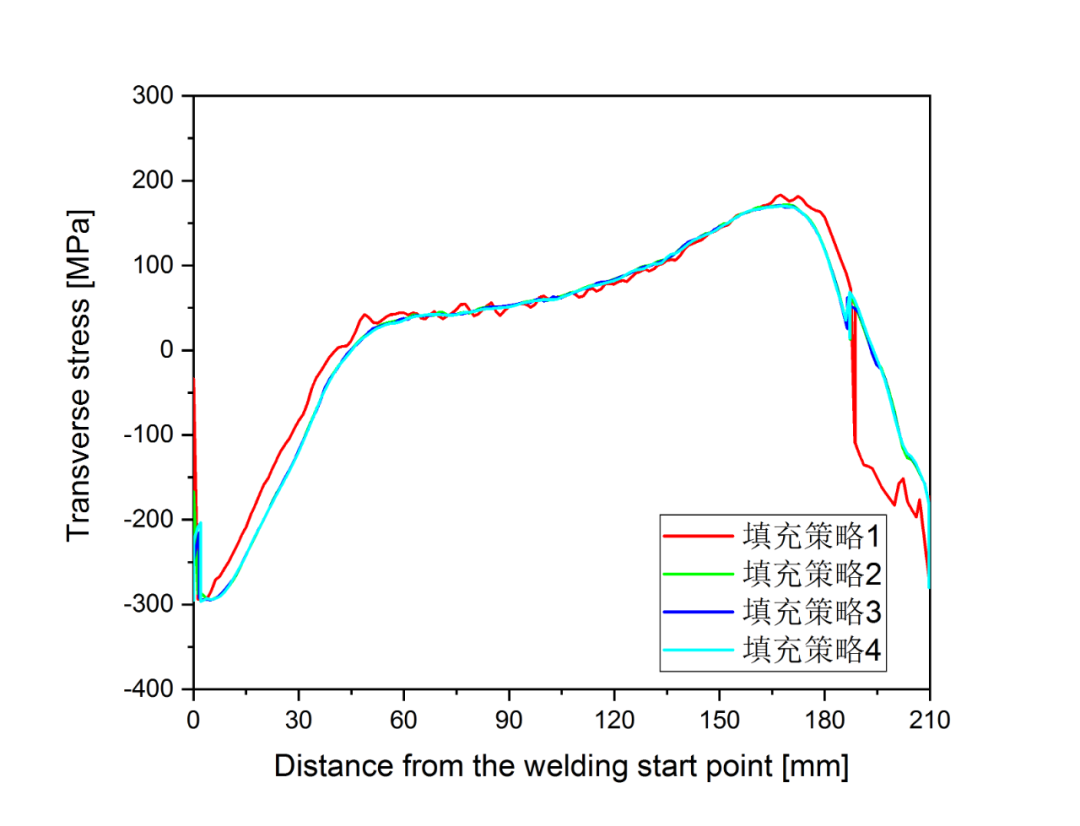
图3.9 不同填充策略下沿焊接方向的横向应力

从图3.9中可以看出，除填充策略1与其余三种有较大差异之外，通过填充策略2、3、4得到的应力分布基本是完全吻合的，这表明在保证焊缝区域的填充金属相能够完全转变为母材相的情况下，填充过程中的转变温度实际上对应力分布影响非常小。对于本文采用的均匀体热源模型，由于通过该热源模型获得熔池通常较浅，为了保证填充金属相能够完全转变为母材相，应该尽可能设定更低的转变温度，而当温度较低时，又可能由于刚度不协调而出现收敛问题。通过表3.1可以看出，材料的转变温度应不低于1200ºC。从图2.2的弹性模型随温度的变化曲线可得，当温度为1200ºC时，母材的弹性模量为10.836GPa，填充金属的弹性模量为1GPa，因此本文认为填充金属的转变温度应使得母材和填充金属的弹性模量满足以下关系：

其中E_Base为母材的弹性模量，E_Filler为填充材料的弹性模量。

这里，本文仅仅讨论了以温度作为单元激活标准的填充策略，但无论是以距离还是以单元号作为激活标准，都可以通过用户子程序USDFLD非常容易地实现。

4. 结论

本文利用均匀体热源，通过ABAQUS用户子程序USDFLD模拟了T形接头焊接中的焊缝填充过程，并研究了不同的填充策略对计算结果的影响，主要得出的结论如下：

（1）在焊缝填充过程中，应保证焊缝区域的单元全部由填充金属相转变为母材相；在此前提之下，用于控制焊缝填充过程的转变温度值对应力分布的影响非常小；

（2）使用较小的转变温度可能存在收敛问题，在填充金属完成转变时，应保证母材相的弹性模量不大于填充金属相的0.1倍。