无限元在Abaqus静力分析中的应用
分析人员有时会面临无限大空间中的边值问题,或者是感兴趣的区域相比于周围介质非常小的情况。无限元旨在通过与常规的一阶或二阶平面、轴对称或三维实体单元混合使用来解决此类问题,即通过常规单元模拟感兴趣的区域,而远场边界则通过无限元来模拟。此外,在动力分析中,无限元还可以用来吸收应力波,防止在边界处反射回来的应力波对计算结果产生影响。本文主要讨论无限元在非线性有限元软件Abaqus的静力分析中的应用。

-01-
无限元基本原理
1.1
一维无限元
Abaqus中用于静力分析的无限元是参考Zienkiewicz等人的工作建立的,此类无限元也被称为映射无限元,其特点为采用了两种形函数,即无限元的几何描述通过一组映射函数来实现,而位移场则与常规有限元相同,即采用标准的形函数来确定。
1.1.1 坐标的映射变换
假定无限元具有方向性,单元从x1开始,经过x2,并延伸至无穷远处的x3。然后将该单元映射到自然坐标ξ表示的有限域上(-1≤ξ≤1)。如图1所示。
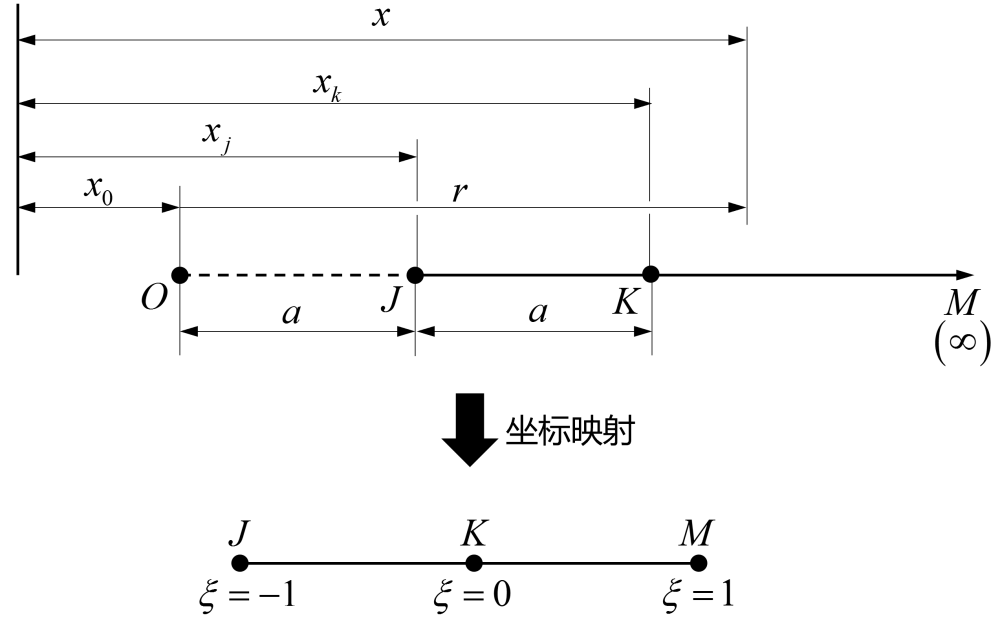
图1 映射到自然坐标系的无限元
“极点(pole)”O相对于全局坐标的位置x0是任意的,一旦确定下来,则节点K的位置可表示为:
定义全局坐标x与自然坐标ξ之间的映射关系为:
式中:
不难验证
并且满足
显然Mj和Mk分别为一维无限元中节点J和节点K的形函数,图2给出了形函数Mj和Mk随自然坐标的变化。
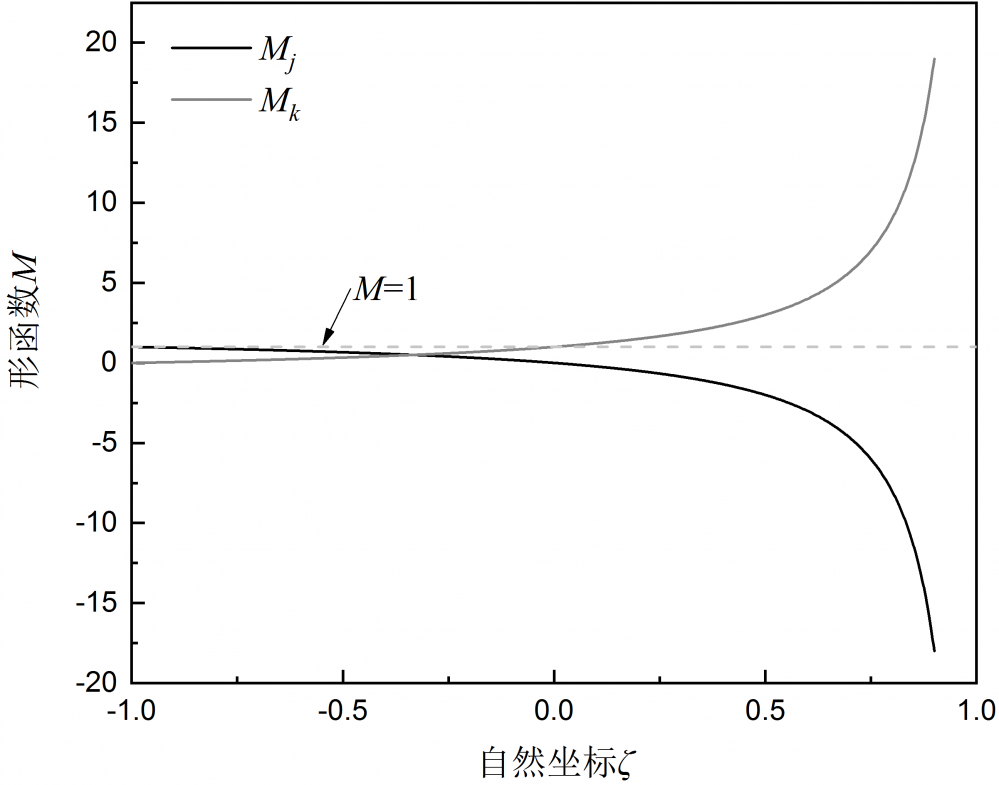
图2 形函数随自然坐标的变化
可以看到
定义无限元上任意一点到“极点”O为r,则有:
将其代入到全局坐标与自然坐标之间的变换关系:
可以得到:
1.1.2 单元的位移模式
设节点J、K和M的位移自由度分别为u1,u2和u3,则采用3节点等参单元的标准形函数可以得到任意一点处的节点位移可表示为:
将ξ与r的关系代入上式可得:
当ξ趋近于1,即当r趋近于无穷远时,则位移u趋近于u3,如果令无穷远处的位移为零,即u3=0,则该无限元的形函数可重新表示为:
并且需要注意的是,当位于极点O时,即x=x0(r=0),可以得到极点处的位移趋于无穷大,是一个奇异点。
1.2
二维无限元
1.2.1 坐标的映射变换
下面以5节点的二维无限元为例,该单元的6,7,8节点在无穷远处,利用一组映射函数将其映射到自然坐标系中,如图3所示。

图3 映射到自然坐标系的二维无限元
则全局坐标x和y与自然坐标ξ和η之间的变换关系为:
式中,Mi为映射函数,分别为:
不难验证在不同节点处各个映射函数的取值如表1所示。
表1 不同节点处各个映射函数的取值
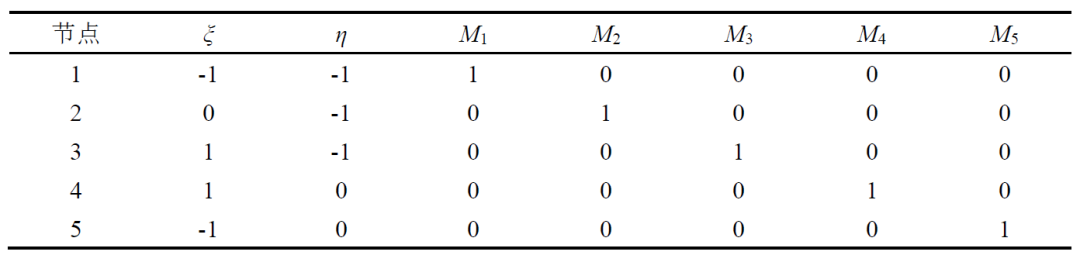
并且当η=±1时,Mi=∞,因此有:
即实际单元相应的边界位于η方向的无穷远处。
1.2.2 单元的位移模式
为了使5节点映射无限元与8节点四边单元在相邻边正常连接,需要使用8节点四边形等参元的形函数,即:
当然,与1.1.2节类似,如果令无穷远处(即节点6、7、8)的位移自由度为零,则只需用到节点1到节点5的形函数,即有:
设节点位移列阵为:
则单元的位移场可表示为:
式中:
1.2.3 单元应力和应变
由弹性力学平面问题的几何方程可得单元应变为:
上式可简记为:
式中:[∂]为几何方程的算子矩阵,即:
需要注意的是,从全局坐标到等参坐标的变换并不会影响应变的值,因此有:
因此可以将单元应变通过节点位移的形式表示出来:
式中:B(ξ, η)为几何函数矩阵,可以表示为:
不难发现,实际上
基于矩阵乘法可得几何函数矩阵B(ξ, η)可表示为:
可以看到,为了简便起见,可以将几何函数矩阵B表示为分块矩阵的形式:
式中:
基于MATLAB的符号变量求偏导功能(diff函数),可以计算得到各个节点的形函数Ni对自然坐标ξ和η的偏导数分别如下所示,并且利用数值梯度函数(gradient)不难验证这些表达式的正确性。
而根据弹性力学中平面问题的物理方程,可得单元应力为:
式中:D为弹性系数矩阵,对于平面应力问题为:
因此有:
1.2.4 单元刚度矩阵
无限元单元刚度矩阵的形成与普通等参元相同,根据单元的能量泛函以及最小势能原理,可以得到单元刚度矩阵的表达式为:
式中:t为平面问题的厚度。
为了便于数值积分,将物理坐标系(x, y)中的刚度矩阵变换到自然坐标系(ξ, η)中进行计算,即有:
式中:|J2|为2阶Jacobian行列式,这里用到了物理坐标与自然坐标之间的变换关系:
这里,与普通等参元不同的地方只是Jacobian矩阵的求解:
同样基于MATLAB的符号变量求偏导功能,可以得到各个节点的映射函数Mi对自然坐标ξ和η的偏导分别为:
因此,基于Gauss-Legendre积分公式,可以将单元刚度矩阵表示为:
因此单元的刚度方程为:
式中:Pe为等效节点载荷矩阵,可表示为:
式中:Pxi和Pyi分别代表作用在节点i上沿x方向和y方向的节点力。
-02-
Abaqus中的无限元
2.1
单元分类
Abaqus针对平面应力/应变、三维应力以及轴对称问题均提供了相应的无限元,对于Abaqus/Standard还可以使用带有减缩积分的无限元。此外Abaqus还提供有声学无限元。无限元在Abaqus单元库中遵循如图4所示的命名惯例。
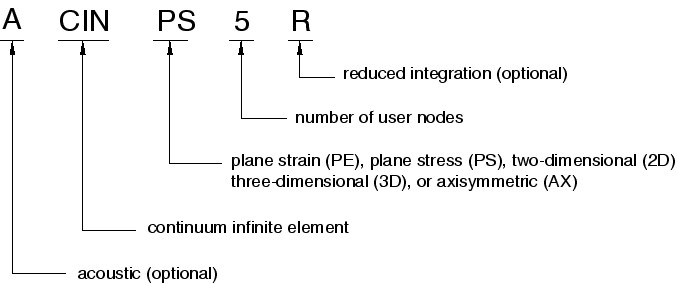
图4 Abaqus无限元命名惯例
例如,CIN3D8代表一个8节点线性实体无限元。
2.2
用于静力分析的无限元的节点定义
由于无限元具有方向性,因此无限元的节点定义方式相比于常规单元有一些特殊的要求。在Abaqus中,无限元的节点编号顺序必须使得无限元的第一个单元面(对于平面单元为第一个单元边)能够与常规单元的单元面(或单元边)连接。例如,图5给出了Abaqus提供的无限元及其节点定义。
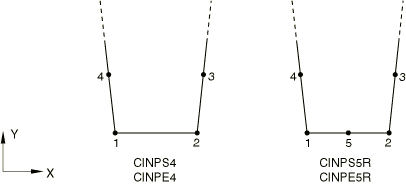
(a)平面应力/应变无限元
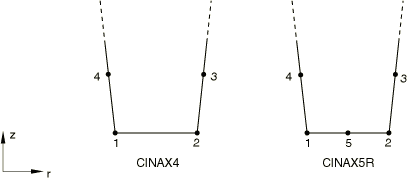
(b)轴对称无限元
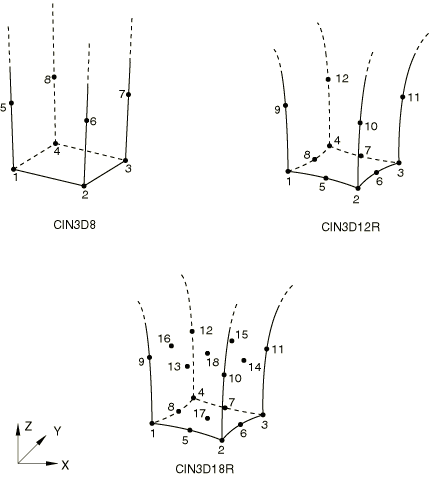
(c)三维无限元
图5 Abaqus提供的无限元
例如,对于图5(a)中的4节点和5节点平面应力/应变无限元,只有4节点无限元的节点1和节点2构成的单元边才能与常规平面应力/应变单元的单元边连接;而在5节点无限元中,只有节点1、节点2以及中间节点5构成的单元边才能与常规的二阶平面应力/应变单元的单元边连接。
此外,在显式动力学分析中,无限元节点中不属于第一个面的区域的处理方式与其他分析有所不同。在无限域的方向这些节点会远离有限元网格。对于显式分析,这些节点的位置是没有意义的,并且在显式动力学分析中不能将载荷和边界条件赋予到这些节点上。但在通用静力分析中,这些处于远离有限元网格区域一侧的节点在单元定义中同样重要,并且能够赋予载荷和边界条件。因此如果无限域存在某些边界条件,如对称约束,则必须在无限元上也赋予相应的边界条件。
从第1节的分析可以看到,远场解会沿着单元边一直延伸到无穷远处,并且会围绕着“极点”作为原点,因此极点起到了定义远场解延伸方向的作用,而极点则是通过非第一个单元面(或单元边)上的节点来定义的。例如,图6给出了弹性半空间域中作用点载荷的情况,从图1中可以看到,节点K到极点O的距离应恰好为节点K到节点J的距离的两倍,因此图6中无限元的布置方式可以恰好使得每个无限元的极点均位于点载荷的作用位置。在静力分析中,极点位置对计算结果存在影响,这一点将在后面通过一个案例进行验证。需注意的是两倍距离的要求是对于静力分析中的无限元而言的,在显式分析中对于远场点到极点的距离则没有要求。
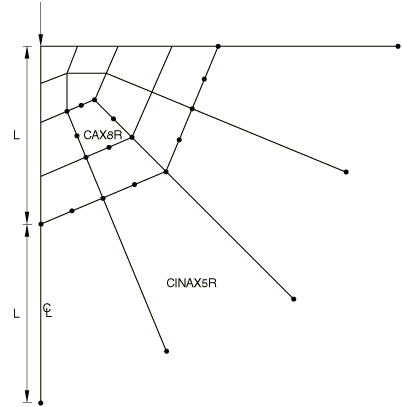
图6 作用在弹性半空间域中的点载荷
此外,出于对该距离的考虑,无限元非第一个单元面(或单元边)的节点应使得延伸到无穷远方向的单元边不会交叉,如图7所示,否则Abaqus将会报错。因此,一种定义无限元的常用方法为首先确定极点的位置,然后根据极点和第一个单元面(或单元边)的节点确定延伸方向,最后根据延伸方向和距离确定非第一个单元面的剩余节点,这样的方法可以保证所有的无限元均围绕同一个极点。
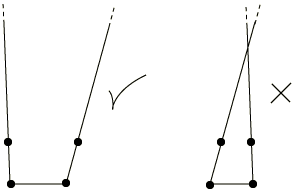
图7 可接受和不可接受的二维无限元
2.3
在平面应力/应变分析中使用二维无限元
下面本文简要介绍如何在平面应力/应变分析中建立包含二维无限元的有限元模型,在三维应力分析中的建立方法可参考该方法进行。以4节点平面应力无限元CINPS4为例,它与常规平面应力单元CPS4具有相同的节点数量,唯一的不同体现在节点顺序的定义上,因为Abaqus要求只能是无限元的第一条单元边与常规单元相连。因此,我们可以在划分网格时将无限元按常规单元处理,而后在inp文件中通过修改单元类型和相应的节点定义来建立无限元。需要注意的是,在Abaqus中单元节点都是以逆时针顺序编号的,例如图8给出了一个常规4节点平面单元的节点定义。
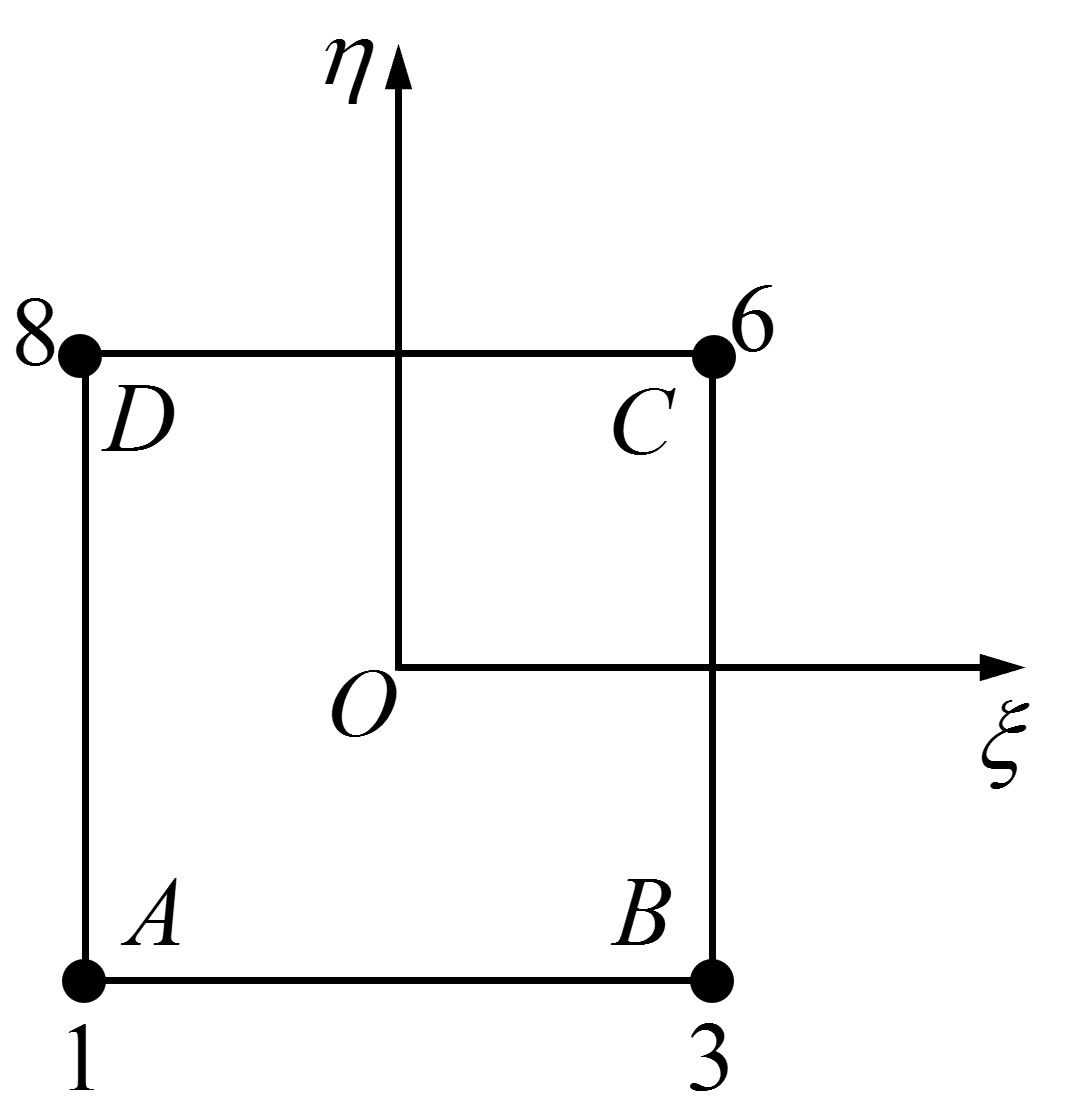
图8 4节点平面单元节点定义
假定该单元的单元号为1,则该单元在inp文件中一种可能的节点定义顺序为:
1, 6, 8, 1, 3
如果将图8中的单元看作是一个无限元,并且节点1和节点3与常规单元连接,则上面的节点定义顺序显然有误,因为此时节点6和节点8构成的单元边为第一条单元边,正确的节点定义顺序应为:
1, 1, 3, 6, 8
显然定义无限元的关键在于确定无限元与常规单元相连接的节点号(下面称为近场边界节点),然后根据这些节点确定节点定义信息中的起始节点(即节点1),由于节点总是按逆时针排序的,因此只要起始节点确定,则其余节点依次排列即可。
一旦确定了常规单元和无限元所在区域,则近场边界节点的编号是已知的,问题转换为如何判断起始节点,即判断图8中节点1和节点3哪一个为起始节点。
这里我们可以利用向量的叉乘进行判断,若单元形心为O(可以通过四个节点的坐标确定),并且节点A和节点B与形心O构成的向量分别为u和v:
则两个向量的叉乘可表示为:
若
则B点位于A点的逆时针方向,因此起始节点编号应为A点的节点编号,否则应为B点的节点编号。基于上述方法,本文通过MATLAB编制了无限元节点处理程序,可以基于待生成无限元的常规单元的单元号、近场边界节点号以及节点定义信息自动生成无限元的定义信息,程序及相应的建模过程参见附录。
2.4
计算示例:含中心穿透裂纹的无限大平板
考虑一块含中心穿透裂纹的无限大平板,在整个裂纹面上作用有单位均布载荷,下面通过有限元法计算外载作用下的裂纹张开位移,并与理论解进行对比。
考虑到几何以及边界条件的对称性,可以仅建立四分之一有限元模型,并在相应的边界上施加对称约束,本文建立的有限元模型如图9所示。Abaqus为了用户便于区分无限元和常规单元,将无限元设置为仅显示三条单元边,需要注意的是,即使是无限元,也需要在相应的节点上施加对称约束。
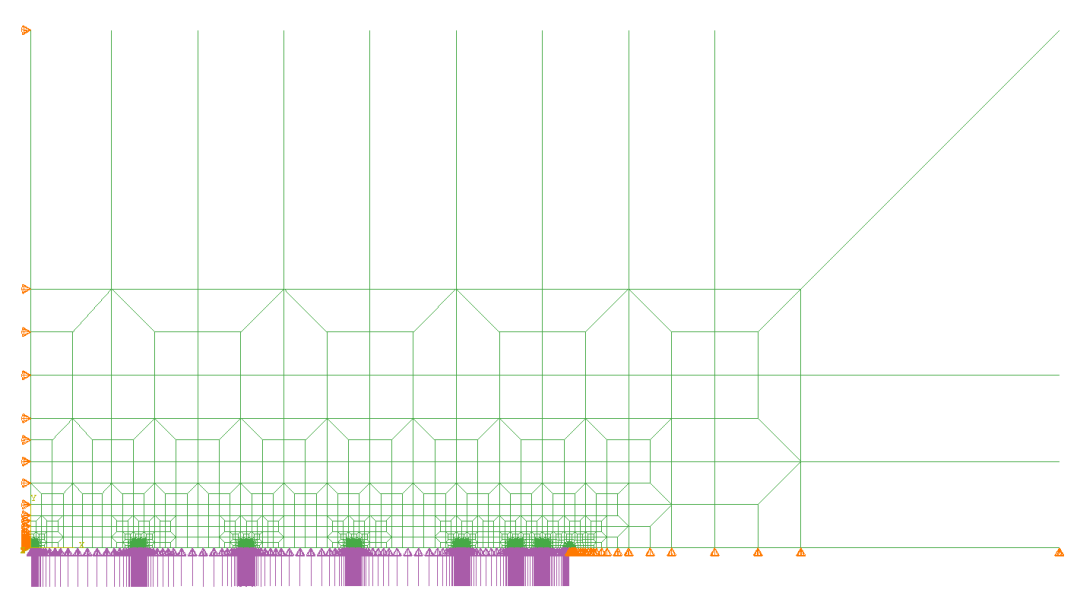
图9 含中心穿透裂纹的无限大板有限元模型
2.4.1 无限元布置方式对裂纹张开位移的影响
为了研究无限元布置方式对计算结果的影响,本文考虑如图10所示的两种无限元布置方式,其中布置方式1仅在x向和y向布置无限元,而未在斜向布置无限元,而布置方式2则在三个方向上均布置有无限元。
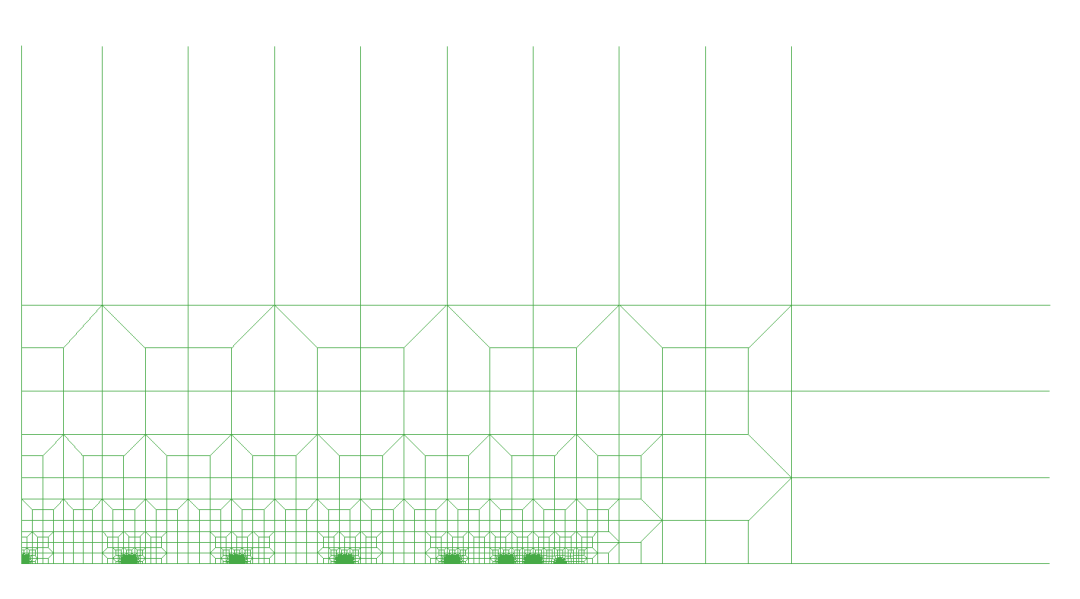
(a)布置方式1
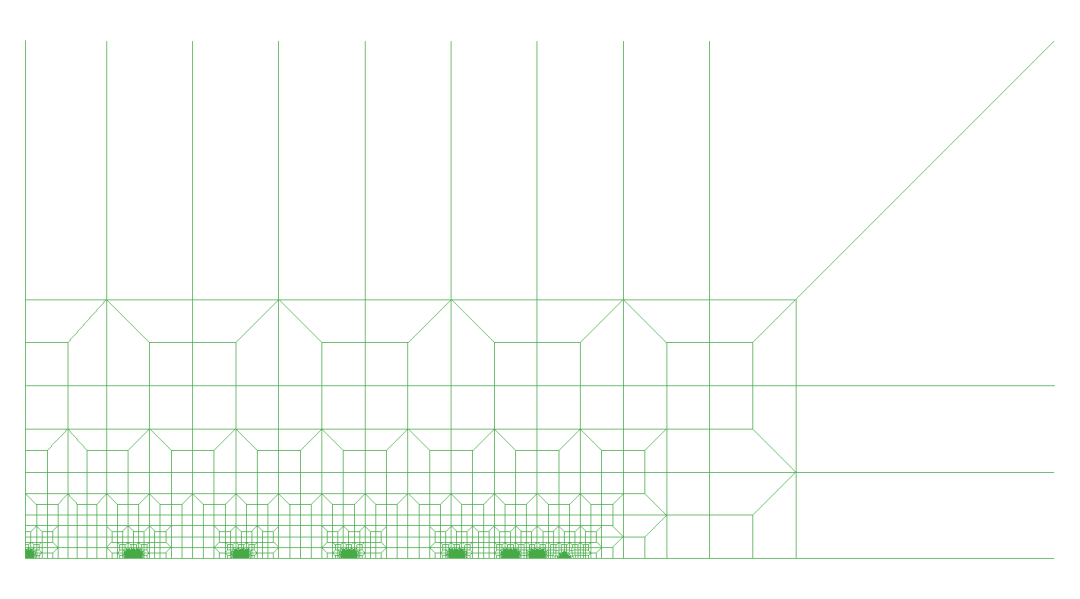
(b)布置方式2
图10 二维无限元布置方式
图11给出了通过两种无限元布置方式获得的裂纹张开位移,从图中可以看到,两种布置方式得到的裂纹张开位移曲线差异较大,并且与解析解存在一定偏差,这说明布置方式1虽然易于实现,但并不能很好地模拟无限域边界。虽然布置方式2也与解析解存在较大偏差,但本文认为这主要是由于基体(常规单元划分的区域)尺寸设置较小所带来的精度损失。
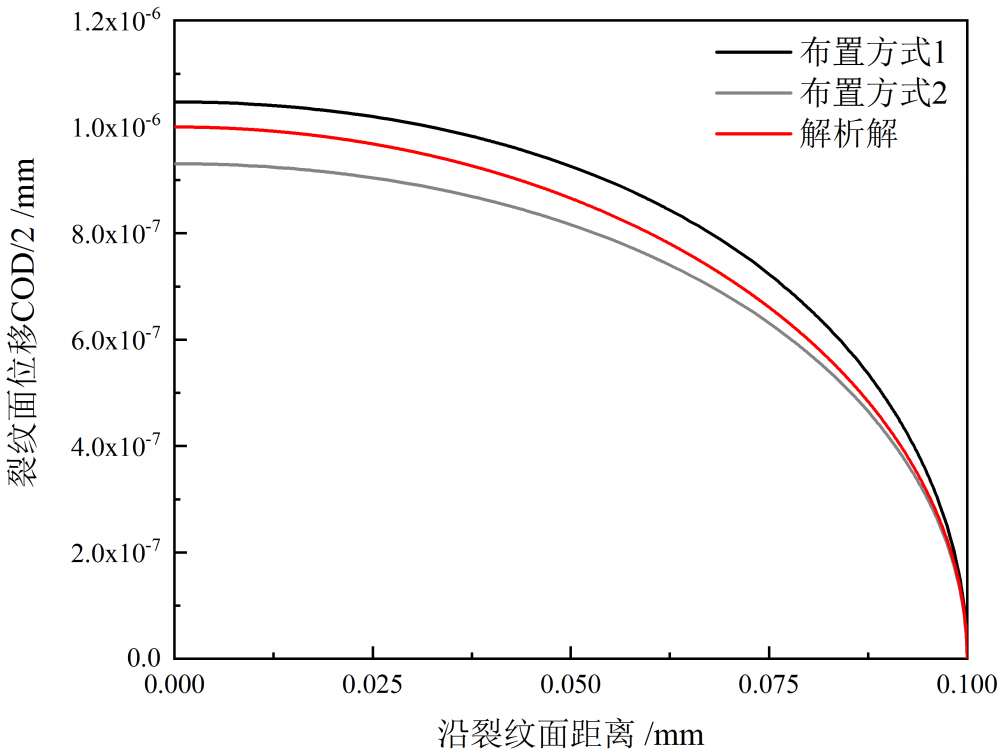
图11 无限元布置方式对裂纹张开位移的影响
2.4.2 基体尺寸及极点位置对裂纹张开位移的影响
为了比较分析基体尺寸及极点位置对计算结果的影响,本文分别计算了大尺寸基体和小尺寸基体中极点取不同位置(即无限元的单元长度)时的裂纹张开位移,结果如图12所示。

图12 基体尺寸及极点位置对裂纹张开位移的影响
从图12中可以看到,在小尺寸基体中,极点位置对计算结果存在很大的影响;而在大尺寸基体中,两种极点位置下的裂纹张开位移曲线完全吻合,并且与解析解非常接近,这说明计算结果对极点位置并不敏感。
从上述分析可以看到,虽然无限元在静力分析中可以用于模拟无限域,但仍需要划分足量的常规单元来模拟远场边界,使得靠近有限元与无限元的界面处的应力已经趋于平缓。并且,在布置无限元时,应使得无限元包围整个代表无限域的区域,而不存在空隙,例如图13给出了用三维无限元代表无限域的情况,否则即使使用无限元也会给出不精确的计算结果。

图13 含三维无限元的网格模型
参考文献
[1] O. C. Zienkiewicz, C. Emson, P. Bettess. A novel boundary infinite element[J]. International journal for numerical methods in engineering, 1983, 19, 393-404.
[2] 赵宇. 映射无限元在工程中的应用[D]. 广西: 广西大学, 1999.
[3] 曾攀. 有限元分析及应用[M]. 北京: 清华大学出版社, 2004.
[4] Dassault Systemes. ABAQUS 6.14 Analysis user’s guide[M].
END
附录:二维无限元节点编号处理程序
clear,clc%程序用于将Abaqus常规4节点平面单元转换为4节点单向映射无限元%************************读取基本数据**************************************%读取模型节点编号Node_id_data=importdata("Node_id.txt");%读取用于生成无限元的4节点平面单元的编号Inf_elem_data=importdata("Inf_elem_node.txt");%读取无限元近场边界(与常规单元相连的边界)上的节点(需要按顺序排列)BC_node=importdata("BC_node.txt");%整理边界节点数据为一维数组并剔除NaN数据BC_node_num=size(BC_node,1)*size(BC_node,2)-sum(sum(isnan(BC_node)));BC_node_data=zeros(BC_node_num,1);k=1;for i=1:size(BC_node,1)for j=1:size(BC_node,2)if isnan(BC_node(i,j))continue;elseBC_node_data(k)=BC_node(i,j);k=k+1;endendendclear BC_node%**************************************************************************%*******************遍历4节点平面单元生成4节点无限元***********************fileID=fopen("Inf_elem_def.txt","w");Inf_elem_num=size(Inf_elem_data,1);for i=1:Inf_elem_numInf_elem_id=Inf_elem_data(i,1);%遍历当前单元的每一个节点 寻找属于近场边界的节点BC_node_current=zeros(2,1);k=1;for j=1:4if find(Inf_elem_data(i,j+1)==BC_node_data(:))BC_node_current(k,1)=Inf_elem_data(i,j+1);k=k+1;endend%根据逆时针编号顺序确定边界起始节点号%获取当前单元四个节点的坐标Node_Coord_X=zeros(4,1);Node_Coord_Y=zeros(4,1);for j=1:4%计算当前节点在节点定义信息中的索引号index=find(Inf_elem_data(i,j+1)==Node_id_data(:,1));Node_Coord_X(j)=Node_id_data(index,2);Node_Coord_Y(j)=Node_id_data(index,3);end%计算当前单元的中心坐标Node_Center_X=sum(Node_Coord_X)/4;Node_Center_Y=sum(Node_Coord_Y)/4;%计算当前单元位于边界的节点的坐标BC_node_Coord_X=zeros(2,1);BC_node_Coord_Y=zeros(2,1);for j=1:2index=find(BC_node_current(j)==Node_id_data(:,1));BC_node_Coord_X(j)=Node_id_data(index,2);BC_node_Coord_Y(j)=Node_id_data(index,3);end%计算边界节点与中心坐标形成的矢量BC_node_vector_I=[BC_node_Coord_X(1)-Node_Center_X;...BC_node_Coord_Y(1)-Node_Center_Y];BC_node_vector_J=[BC_node_Coord_X(2)-Node_Center_X;...BC_node_Coord_Y(2)-Node_Center_Y];%计算两个矢量的叉乘Cross_mult=(BC_node_vector_I(1)*BC_node_vector_J(2)-...BC_node_vector_I(2)*BC_node_vector_J(1));%根据叉乘正负判断无限元节点顺序编号的起始节点if Cross_mult>0BC_node_start=BC_node_current(1);elseBC_node_start=BC_node_current(2);end%根据起始节点重新依照逆时针顺序进行编号Inf_elem_def=zeros(5,1);index_start=find(BC_node_start==Inf_elem_data(i,:));Inf_elem_def(1)=Inf_elem_data(i,1);Inf_elem_def(2:2+5-index_start)=Inf_elem_data(i,index_start:end);Inf_elem_def(8-index_start:end)=Inf_elem_data(i,2:index_start-1);%输出无限元定义信息for j=1:5if j==5fprintf(fileID,"%10d\n",Inf_elem_def(j));elsefprintf(fileID,"%10d,",Inf_elem_def(j));endendendfclose(fileID);%**************************************************************************




