MATLAB如何输出高质量图片
矢量图与像素图
在我们撰写学术论文时,图表是展示我们学术成果的重要载体。因此,在保证内容质量的前提下,绘制一张精美的图片,往往可以使得我们的论文在投稿更容易得到编辑的青睐。目前,科研人员向出版社提交的图片可以分为矢量图(Vector image)和像素图(Pixel image)两类。
构造基础
像素图的构造基础为若干个方块形状的像素点,在每个像素点上存储有图片的颜色信息,如RGB值等。对于像素图,如果我们将图片放大到足够的倍数,就可以看到构成图片的这些小方块。
而矢量图的构造基础为通过图形学数学表达式描述的线条和曲线(点、线、多边形和圆弧等),并通过线条颜色以及填充封闭曲线的颜色来描述图形的颜色。
常用文件格式及编辑软件
目前,像素图的常用文件格式主要包括JPG,PNG,BMP和EPS等,常用的编辑软件为Adobe Photoshop,Word,PowerPoint等。
矢量图的常用文件格式为EMF,WMF,EPS和SVG等,常用的编辑软件为Adobe Illustrator,Word,PowerPoint和CorelDRAW等。注意这些文件格式中,EPS为Adobe系列软件的专有格式,而EMF和WMF为Office系列软件的专有文件格式。
优缺点分析
像素图的清晰程度取决于像素点的数量,因此对于分辨率越高的图片,其占用的存储空间也就越大;而矢量图由于采用了公式化的描述方式,因此图片大小不取决于像素和分辨率,这也使得矢量图的图片大小往往要小于像素图,但其缺点为难以表现色彩层次丰富的逼真图像效果,不易制作色调丰富或色彩变化太多的图像,而且绘制出来的图形不是很逼真,无法同像素图一样精确地描述各种相对复杂的图形(如真实的自然风景等)。
对于学术论文而言,其涉及的图表大多数是用来呈现数据,点线图、柱状图和云图等是主要的呈现方式。因此,使用高度清晰且不占用过多存储空间的矢量图相比于像素图更具优势。下面,本文主要介绍采用MATLAB进行数据分析时,如何输出高质量的矢量图片。
矢量图片输出方法
MATLAB直接输出
对于简单线条和曲线构成的点线图等,我们可以直接通过MATLAB进行输出。我们可以在图形窗口中选择文件→导出设置,在渲染属性中勾选自定义渲染器,并将其更改为painters (向量格式),如下图所示。
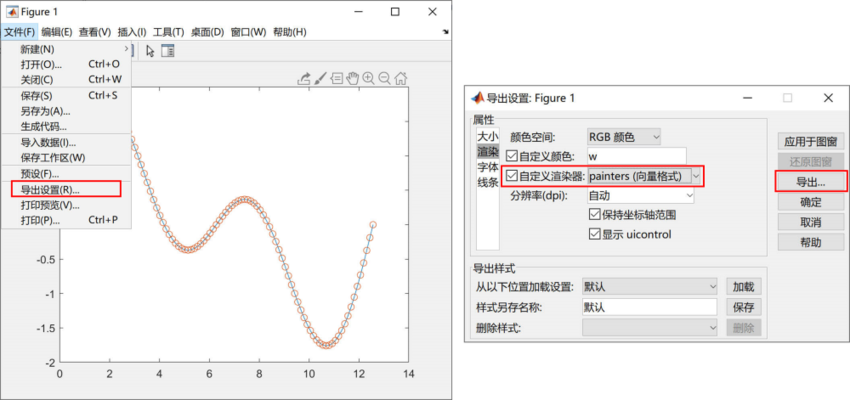
更改完成后,点击导出,并选择需要输出的矢量文件格式,即可输出矢量图片。如果需要对图片进行后续修改,建议将图片导出为EPS格式,并通过Adobe Illustrator进行编辑;如果需要在Word或PowerPoint中编辑,则应选择保存为EMF文件格式,如下图所示。
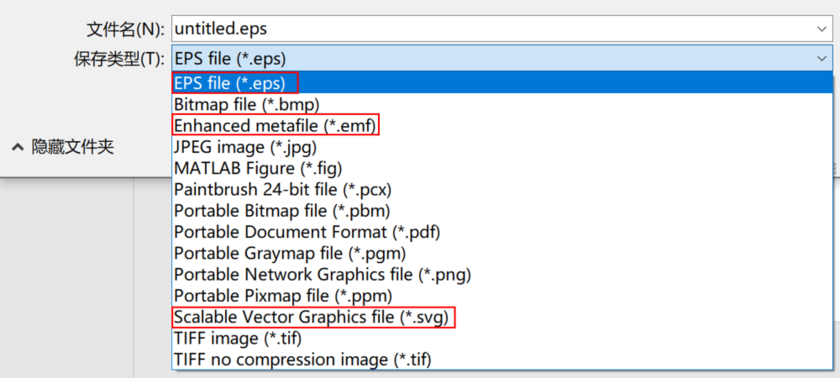
exportgraphics函数输出
对于MATLAB 2020a以上版本,MATLAB提供了exportgraphics函数用于将图片输出为文件格式。例如,下面的代码给出了一个通过exportgraphics函数输出EPS文件的简单示例:
x=linspace(0,1,101);y=sin(x);
plot(x,y);
exportgraphics(gcf,'imagefile.eps','ContentType','vector')
这里,gcf代表当前图形对象(Figure1)的句柄值,vector表示以矢量形式输出。关于exportgraphics函数的更多用法可以参见帮助文档。
对于没有MATLAB 2020a以上版本正版授权的用户,可以尝试使用MathWorks公司提供的MATLAB在线版。
只需注册一个MathWorks的账号,即可享受每个月20小时的免 费 使 用时长,足以满足一般的绘图需求。
MATLAB与Tecplot结合
需要注意的是,对于MATLAB 2019以下的版本,如果采用surf等函数绘制三维曲面图,笔者发现即使指定输出格式为矢量文件格式也无法得到矢量图,这可能是由于MATLAB未完善相关功能所引起的。此时可以采用MATLAB与有限元后处理软件Tecplot结合的方式来输出矢量图。以曲面的绘制为例,首先我们在MATLAB中生成一组数据并绘制三维曲面图:
x=linspace(0,pi,11);y=linspace(0,2*pi,11);[X,Y]=meshgrid(x,y);
Z=sin(X).*cos(Y);
surf(X,Y,Z);对于MATLAB 2019以下版本,如果按照前面介绍的方法来导出矢量图片,可以发现图片在放大到一定倍数后,其线条呈现明显的锯齿状,如下图所示。这说明该图实际上是一张像素图。

为解决该问题,这里介绍一种通过Tecplot绘制曲面图的方法,其绘制思路为将构成曲面的每一个面片看成一个四边形有限元网格,然后借助Tecplot绘制有限元云图的功能来绘制曲面图。因此如果将变量X和Y看作是网格节点坐标,将变量Z看作是节点处的场变量值,则只要给出Tecplot支持的网格定义信息,就可以将其导入到Tecplot中完成曲面图的绘制。网格定义信息的构建可以基于笔者编写的函数实现(函数源代码参见附录),其调用方式如下所示:
Mesh_Generator(X,Y,Z);执行该函数后将生成一个名为Mesh_Visual.dat的文本文件,在Tecplot中通过File→Load Data导入该文件,切换绘制方式为三维笛卡尔坐标系(3D Cartesian),在Show zone layers中勾选Mesh和Contour,并通过Plot→Axis添加三向坐标轴,即可绘制曲面图,如下图所示。
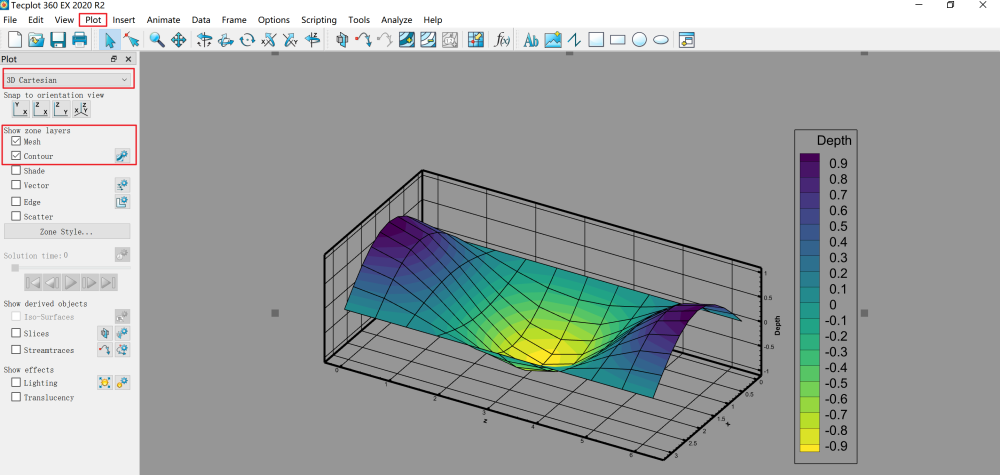
Tecplot中可以对曲面图的坐标范围和图例颜色等进行非常详细的设置,关于Tecplot的更多介绍可以参见《基于临界平面法的多轴疲劳分析》。设置完成后,选择File→Export即可导出矢量图片,如下图所示。
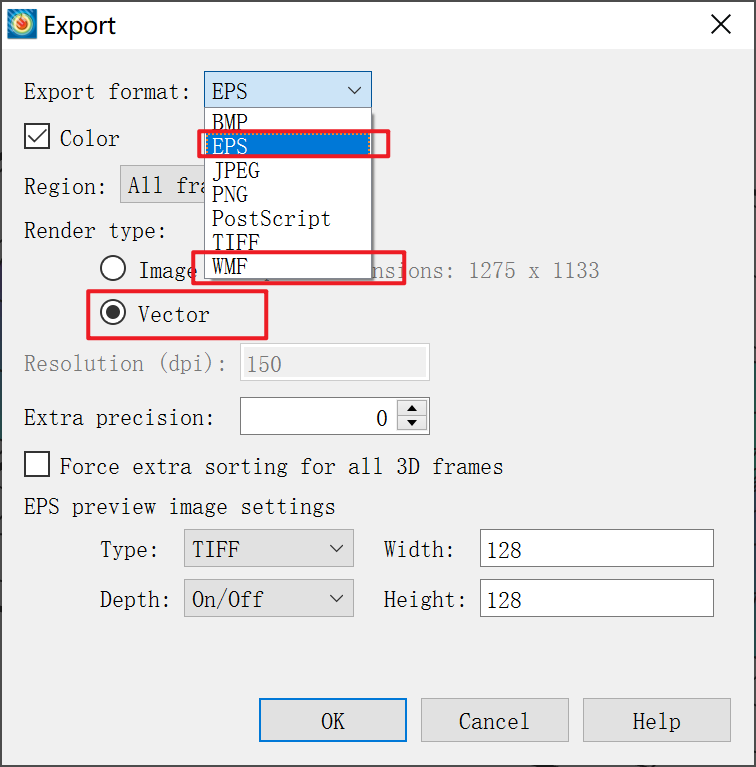
最终导出的矢量图片如下图所示。

为了在微 信公众平台获得最佳的显示效果,上图是通过Tecplot导出EPS文件,并利用Adobe Illustrator转换为SVG文件实现的,SVG文件格式是微 信公众平台唯一支持的矢量图片格式。在手机上放大该图片(以浏览器模式打开网页并切换为桌面版网站)可以发现该图片可以无限放大并仍然保持足够的清晰度。
需要注意的是,采用MATLAB与Tecplot结合的方式只能绘制一些简单的云图或曲面图,对于更为复杂的图形,建议尝试在最新版的MATLAB中通过exportgraphics函数绘制。
附录
%程序用于导入网格数据到Tecplot软件
function Mesh_Generator(X,Y,Z)
%*****************************构造网格定义信息*****************************
[Num_Node_y,Num_Node_x]=size(Z);
%构造单元定义信息数据(数组索引为单元号 数组元素为顺序排列的节点号)
Elem_connect=zeros((Num_Node_x-1)*(Num_Node_y-1),4);
k=1;
for i=1:Num_Node_y-1
for j=1:Num_Node_x-1
Elem_connect(k,1)=(Num_Node_x*(i-1))+j;
Elem_connect(k,2)=(Num_Node_x*(i-1))+j+1;
Elem_connect(k,3)=(Num_Node_x*i)+j+1;
Elem_connect(k,4)=(Num_Node_x*i)+j;
k=k+1;
end
end
%构造节点定义信息(数组索引为节点号 数组元素为坐标x和y)
Node_X=reshape(X',[Num_Node_x*Num_Node_y,1]);
Node_Y=reshape(Y',[Num_Node_x*Num_Node_y,1]);
%生成轮廓高度信息的节点值
Node_Height=reshape(Z',...
[Num_Node_x*Num_Node_y,1]);
%**************************************************************************
%*********************输出网格定义信息至Tecplot文件************************
File_Tecplot_id=fopen("Mesh_Visual.dat","w");
%输出基本信息
fprintf(File_Tecplot_id,'title=\"Mesh Visualization in 2D FEM\"\n');
fprintf(File_Tecplot_id,'variables=\"x\",\"z\",\"Depth\"\n');
fprintf(File_Tecplot_id,"zone I=%d,J=%d,F=POINT\n",...
Num_Node_x,Num_Node_y);
%输出网格信息
for i=1:size(Node_X,1)
fprintf(File_Tecplot_id,"%f ",Node_X(i));
fprintf(File_Tecplot_id,"%f ",Node_Y(i));
fprintf(File_Tecplot_id,"%f\n",Node_Height(i));
end
fclose(File_Tecplot_id);
%**************************************************************************
end



