DFT之泄露
(1)漫画


(2)引言
自从同事给推荐Understanding Digital Signal Processing这本书来,断断续续地一直再看。最近,终于看的稍微明白了一点。
这章共看了三遍:
(1) 看第一遍的时候,就是不管懂不懂,先往下看,所以看完后,感觉就像没看一样;
(2) 看第二遍的时候,就边看边翻译成中文,有不懂的,也放过;但是因为有形成文档笔记,所以本身心里还是比较有成就感的。这样就形成了正循环,看的时候,心情比较愉悦,所以理解的东西也会比较容易。
(3) 看第三遍的时候,就尝试着用自己的语言组织,用matlab去仿真验证,不懂的再去查其他资料帮助理解。
不得不说,写公 众 号确实是一个促进学习的好方式,以写促学。因为想在公 众 号里发表出来,就会去很认真地去写文档,然后就会把那些似懂非懂的问题去搞懂。
根据书本上的DFT上的内容,共整理了以下几篇文档:
DFT学习笔记,是关于DFT的变换公式以及其的一些特性
DFT之泄露,关于泄露的现象以及产生的原因;
DFT之窗函数,列举了几种窗函数,并进行了相关比较,以及窗函数的一些作用
DFT之扇贝损耗,以矩形函数为例,叙述了扇贝损耗的现象
DFT之零填充,指出进行零填充的原因,以及注意事项;
DFT之处理增益;
第一篇可以从往期文章看到,今天这篇主要是关于泄露。
(3)DFT之泄露
泄露的现象
DFT即是,对具有N个数的输入序列,进行一个N点的DFT变换,产生一个具有N个点的频域序列。而且,这些频域序列的间隔为:
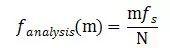
前面的例子DFT学习笔记,之所以能够准确计算出频率,是因为输入信号的频率是fs/N的整数倍。
那如果不是整数倍,会怎么样呢?
还是上面的例子,把第二项的频率从2000改为1500,然后再运行一下程序,可以得到下述结果。并且将频率为2000Hz的计算结果列于左侧。
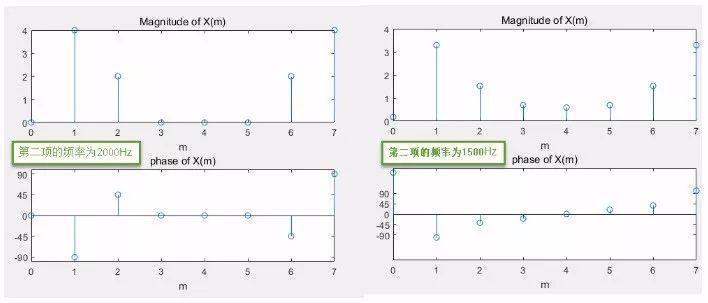
可以看到:
(1) 在m=1.5处未产生频谱,
(2) m=2,3,4,5处应该是0的,现在也有值了
(3) m=1,7处的值与频率为2000Hz时的结果相比,变小了。
从上面例子可以看出,当输入序列的频率不是fs/N的整数倍时,比如1.5fs/N时,其能量会被泄露到频域上的N个序列点上。
因此,在用DFT处理真实世界中的有限长的时间序列时,泄露是不可避免的。
那为什么会产生泄露呢?
这是因为,在使用DFT时,会不可避免的使用窗口函数。
以下列函数为例:
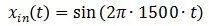
为一连续时间函数。
为了计算其DFT,我们对其以fs=8000对其采样,得到xin[n],即
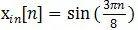
但我们进行DFT运算时,只是使用了其前8个点,记为x[n]。所以可以认为x[n]=xin[n]w[n]。

绘制上图的matlab程序:
clc;
clear all;
ts=1/8000;
N=64;
n=0:1:(N-1);
m=0:1:7;
Xn=sin(2*pi*1500*n*ts);
Xm=sin(2*pi*1500*m*ts);
subplot(3,1,1)
%画原始的连续函数
plot(n,Xn)
title('原始连续函数')
ylabel('xin(t)')
%绘制采样后的函数
subplot(3,1,2)
stem(n,Xn,'k')
hold on;
stem(m,Xm,'r--')
title('黑色为采样后的点,红色为DFT变换所用的点')
ylabel('xin(n)')
%绘制窗函数
subplot(3,1,3)
stem(m,rectwin(8),'b')
hold on;
k=8:1:70
stem(k,zeros(63),'b')
title('矩形窗函数')
ylabel('w(n)')
也就是说,当我们想通过DFT换算计算xin(t)频谱的时候,我们其实是做了这些步骤:
(1) 对连续信号xin(t)进行采样,得到离散信号xin[n]
(2) 截取离散信号xin[n]中的一段,即与窗函数w[n]相乘,得到x[n]。
所以,我们其实计算的是x[n]=xin[n]•w[n]的频谱,即对xin[n]进行矩形加窗后的函数的频谱。
问题是,加窗后的函数的频谱与原来的频谱有什么区别呢?
要说明DFT计算的频谱的问题,先了解一下DFT与DTFT的关系,以及DTFT变换。
DTFT与DFT之间的关系:
DTFT的变换公式为:

DFT的变换公式为:

所以,如果x[n]的长度为L,且L≤N,则其N点DFT为DTFT的采样,即:
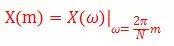
而x[n]正好满足这一要求,所以可以对X(w)做以上操作,以得到其DFT。
时域乘积等于频域卷积。
(1)先计算窗函数的DTFT:
窗函数
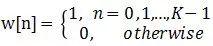
w[n]的DTFT的计算结果为:
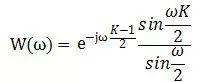
当K=8时,其幅度函数如下图所示:

(2)计算x[n]的DTFT
l 对xin[n]做如下变换:
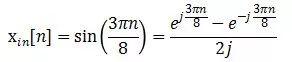
DTFT具有下列性质:
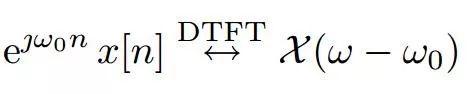
所以

用matlab画出x[n]的DTFT的幅度函数:
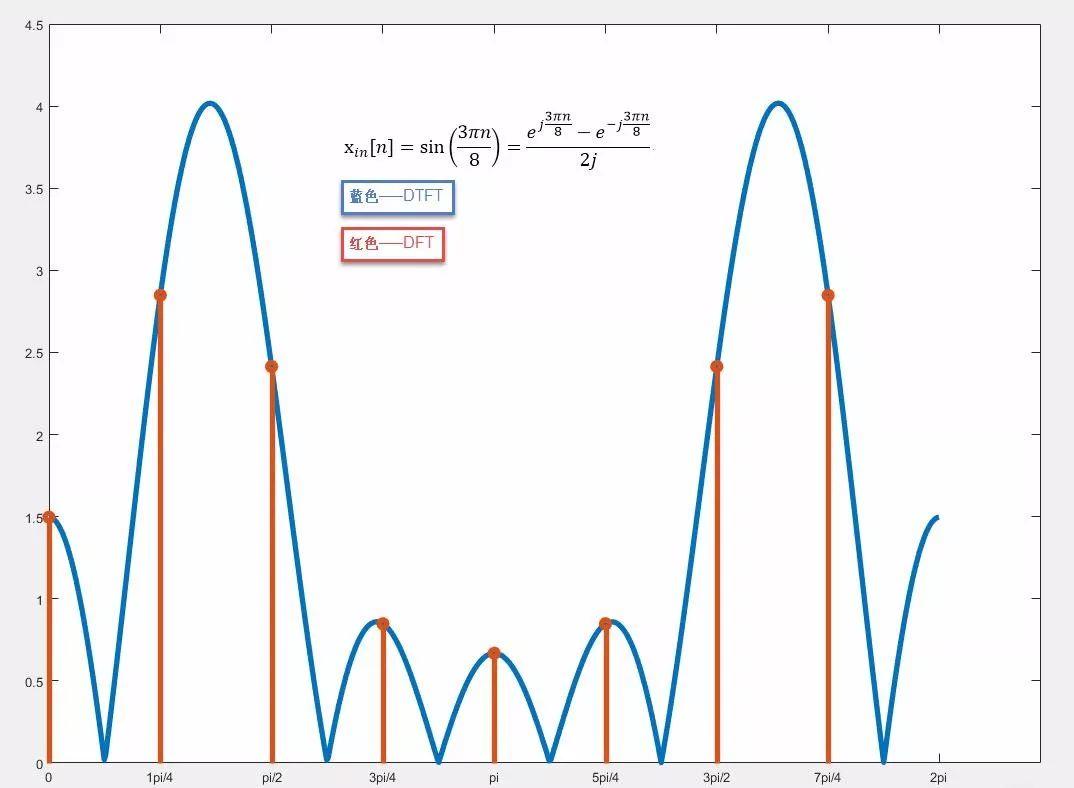
以上两副图的matlab实现程序:
clc;
clear all;
K=8
%计算矩形窗函数DTFT变换的幅度函数
w=-pi:0.01:pi;
Ww=exp(-j*w*(K-1)/2).*sin(w*K/2)./sin(w/2)
figure (1);
plot(w,abs(Ww))
set(gca,'xtick',[-pi:pi/4:pi])
set(gca,'XTickLabel',{'-pi';'-3pi/4';'-pi/2';'-pi/4';'0';'pi/4';'pi/2';'3pi/4';'pi'})
%计算x[n]的DTFT变换
n=0:1:(K-1);
w0=3*pi/8;
xn=sin(w0*n);
ww=0:0.01:2*pi;
w1=ww-w0;
w2=ww+w0;
Ww1=exp(-j*w1*(K-1)/2).*sin(w1*K/2)./sin(w1/2);
Ww2=exp(-j*w2*(K-1)/2).*sin(w2*K/2)./sin(w2/2);
xw=(Ww1-Ww2)/(2*j);
figure (2);
plot(ww,abs(xw));
set(gca,'xtick',[0:pi/4:2*pi])
set(gca,'XTickLabel',{'0';'1pi/4';'pi/2';'3pi/4';'pi';'5pi/4';'3pi/2';'7pi/4';'2pi'})
%计算x[n]的FFT变换,并与x[n]的DTFT变换比较
hold on;
Y=fft(xn,K);
stem(2*pi/K*n,abs(Y))
如果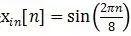 ,则可以得到x[n]的DTFT与FFT之间的关系为:
,则可以得到x[n]的DTFT与FFT之间的关系为:
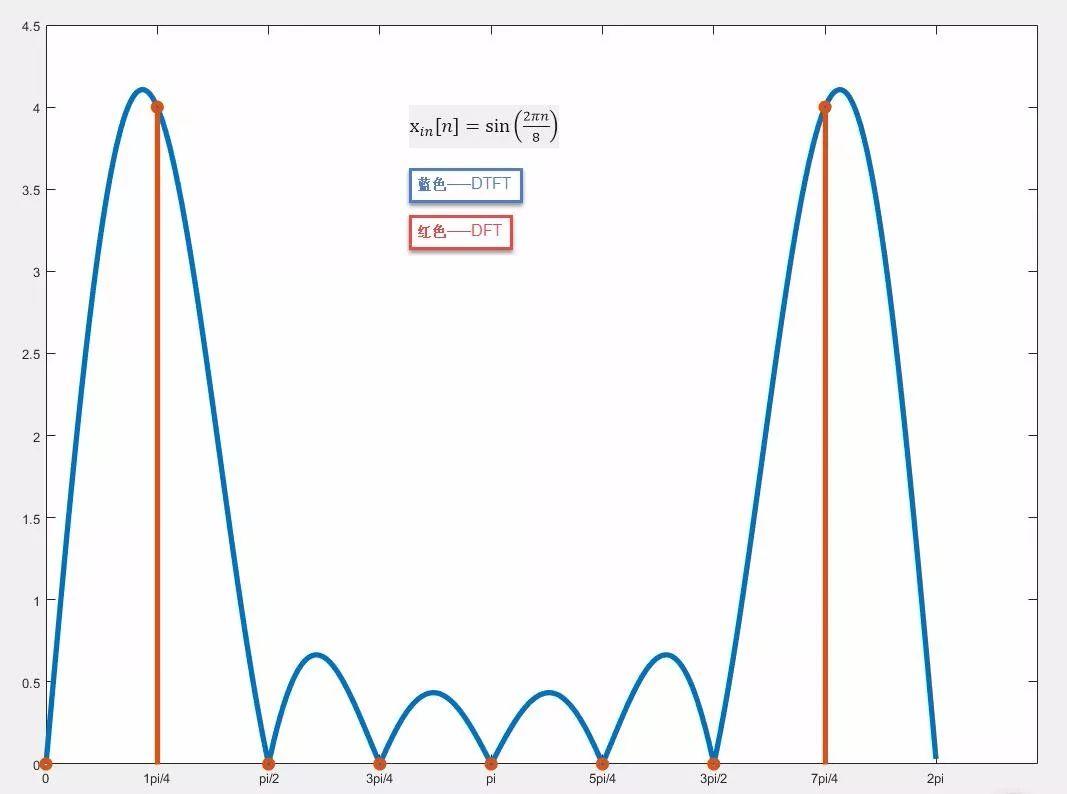
(3)总结说明


从上面两幅图,我们可以看到:
(1) 加窗函数x[n]计算出来的DTFT是连续频谱,也就是说,其包含了所有的频率分量。(2) DFT是在DTFT上采样的结果,如果输入信号的频率正好等于采样点,则计算出来的频率是精确的。
(3) 如果输入信号的频率与采样频率点不等,则计算出来的频率则不等于输入信号频率,而且会有很多泄露。实际情况,经常是这样,输入信号频率≠采样频率点。
所以说,因为窗函数的存在,其旁瓣导致有泄露;所以可以用泄露小的窗函数来减小其影响。
参考文献:
[1]RICHARD G. LYONS Understanding digital signal processing
[2]J. Fessler, chapter 5, The Discrete Fourier Transform




