DFT之窗函数
DFT学习笔记,是关于DFT的变换公式以及其的一些特性
DFT之泄露,关于泄露的现象以及产生的原因;
今天这篇,主要是关于窗函数。
窗函数
为了减小DFT的泄露,需要减小主瓣宽度和旁瓣幅度;理想的窗函数是主瓣宽度窄,旁瓣幅度小。
矩形窗函数首尾值的突变,是其产生旁瓣的原因。所以,可以通过将输入序列的首尾数据平缓连接,以减小旁瓣的幅度,进而减小DFT的泄露。
所以,各种各样的窗函数就被发明了,常用的窗函数有:矩形窗函数、Hanning、Hamming窗函数、Blackman等。
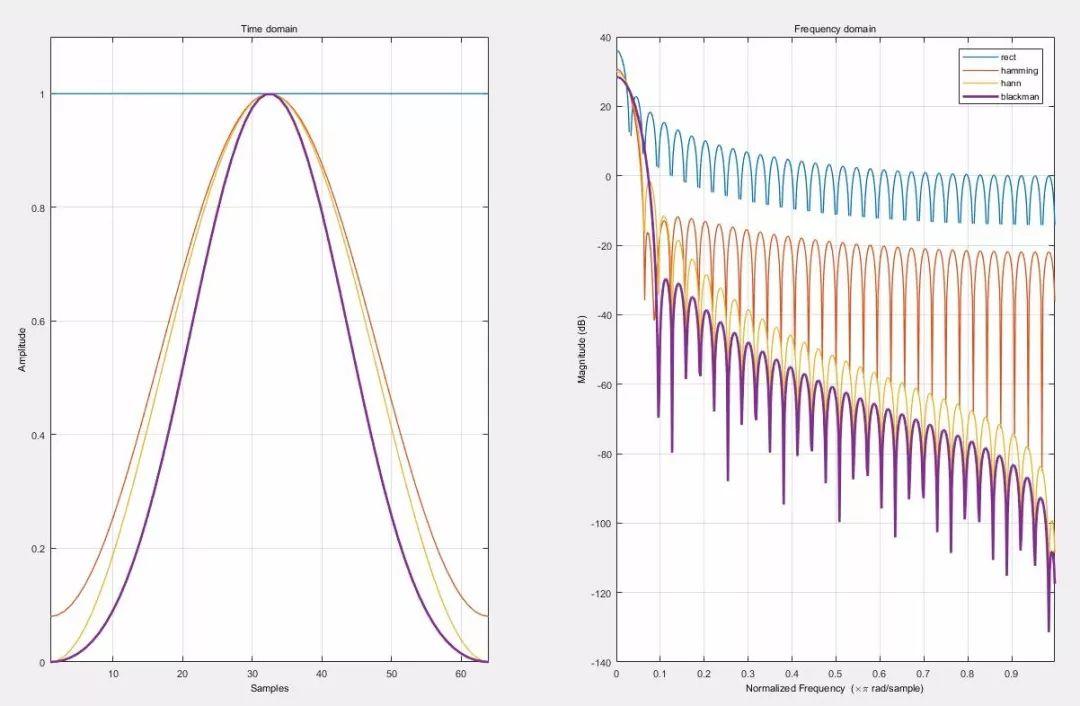
上图是上面四种窗函数的时域和频域的表示。
从频域可以看到,主瓣幅度rect>hamming>hann>blackman,这在时域也比较好理解。
因为Hanning、Hamming和Blackman函数都减小了用于DFT运算的时域信号幅度,所以其主瓣幅度低于矩形窗函数的主瓣幅度,这个幅度损失,称之为处理增益或者处理损耗(processing gain/processing loss)。
将上图中的右图的幅度归一化,可以得到:
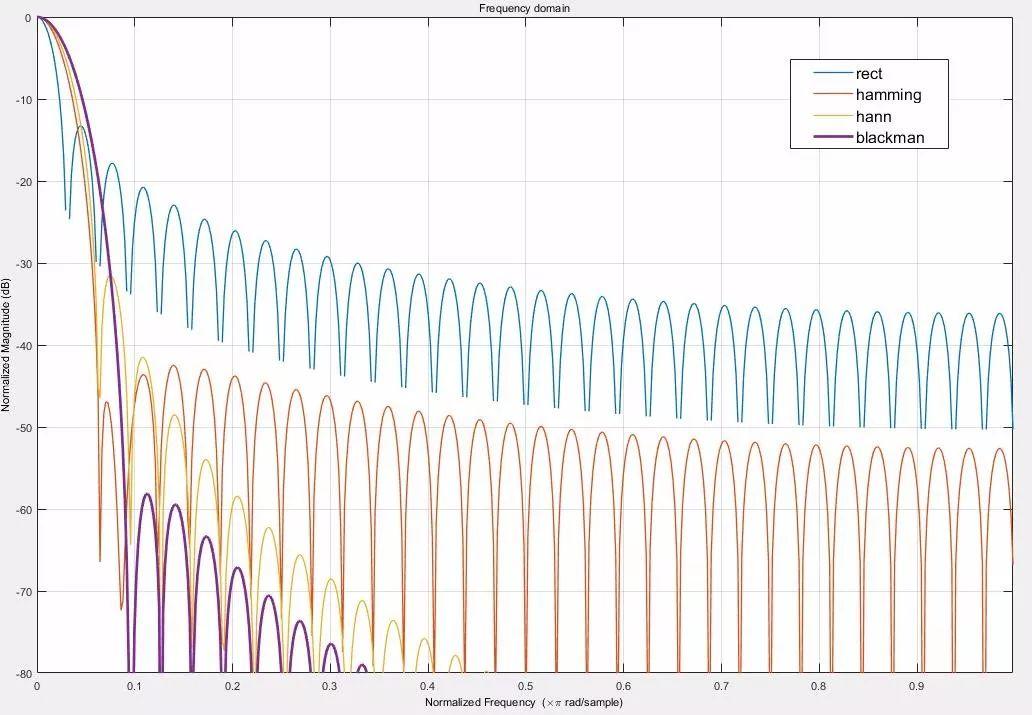
可以看到:
(1) 从主瓣宽度来看:rect<hamming<hann<blackman;
(2) 从旁瓣大小来看:rect>hamming>hann>balckman
对信号加窗函数,有助于我们识别大信号旁边的小信号。
比如,我们对xn=sin(2*pi*1800*n/fs)+0.0001*sin(2*pi*1950*n/fs)做加窗操作,并作2048点的DFT变换,其中fs=8000.
Matlab程序如下:
clc;
clear all;
close all;
K=2048;
n=0:1:K-1;
fs=8000;
xn=sin(2*pi*1800*n/fs)+0.0001*sin(2*pi*1950*n/fs);
figure (1);
plot(n,xn);
figure (2);
subplot(2,2,1);
m=0:1:K/2;
Y=fft(xn'.*rectwin(K),K);
plot(m*fs/K,20*log10(abs(Y(1:(K/2+1)))/max(abs(Y(1:(K/2+1))))),'Linewidth',1)
title('rect')
subplot(2,2,2);
Y1=fft(xn'.*hamming(K),K);
plot(m*fs/K,20*log10(abs(Y1(1:(K/2+1)))/max(abs(Y1(1:(K/2+1))))),'Linewidth',1)
title('hamming')
subplot(2,2,3);
Y2=fft(xn'.*hann(K),K);
plot(m*fs/K,20*log10(abs(Y2(1:(K/2+1)))/max(abs(Y2(1:(K/2+1))))),'Linewidth',1)
title('hann')
subplot(2,2,4);
Y3=fft(xn'.*blackman(K),K);
plot(m*fs/K,20*log10(abs(Y3(1:(K/2+1)))/max(abs(Y3(1:(K/2+1))))),'Linewidth',1)
title('blackman')
运行结果如下图所示:
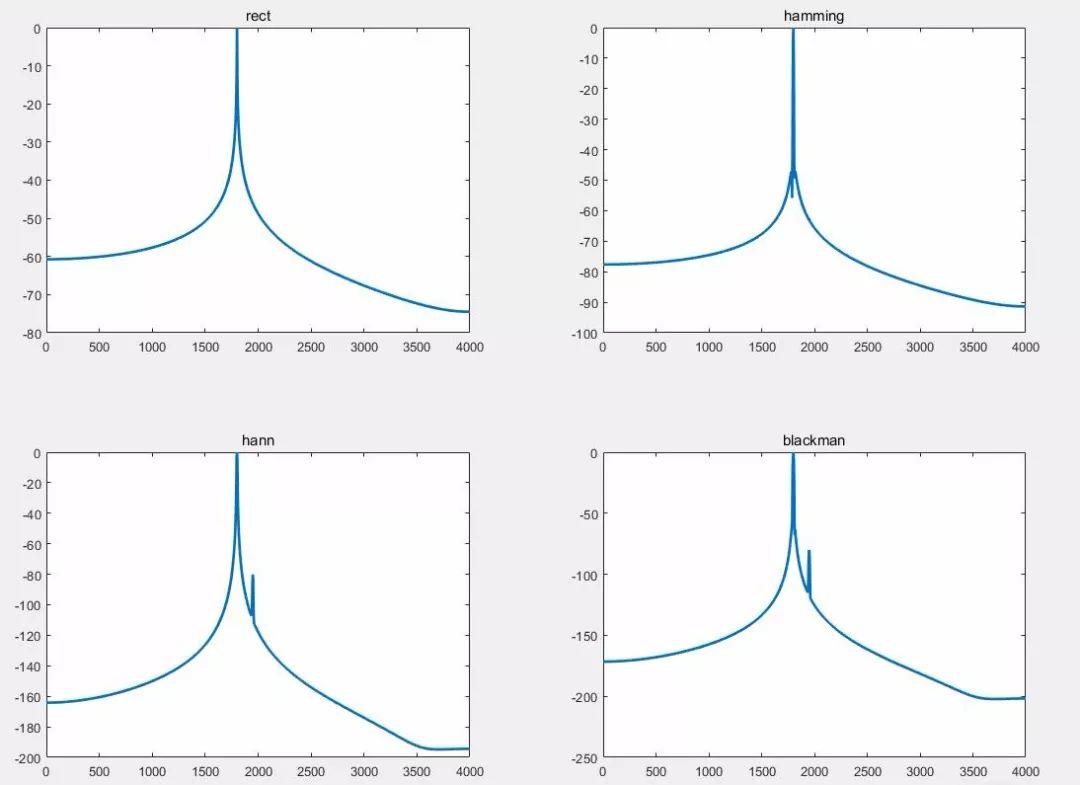
可以看到,如果使用rect和hamming这两种窗函数的话,则不能识别出小信号;但如果用hann或者blackman这两种窗函数的话,则能识别出大信号旁边的小信号。
选择窗函数,需要根据应用情况,在主瓣宽度、第一旁瓣幅度、旁瓣的衰减速度之间的折衷。
参考文献:
[1]RICHARD G. LYONS Understanding digital signal processing
[2]J. Fessler, chapter 5, The Discrete Fourier Transform




