奇妙的运算放大器电路
运算放大器之所以被称为运算放大器,没有叫A放大器或者B放大器,那是因为这种结构可以做运算,比如积分,微分,加法,减法呀等等。
运算放大器有两个输入,一个为同相输入(non-inverting input),记为V+,一个为反相输入(inverting input),记为V-。
运算放大器有一 个输入,记为Vout。
理想情况下,运算放大器只放大两个输入之间的电压差。
那为啥运算放大器会有两个输入呢?这是因为两个输入有两个输入的优点。
(1) 两个输入可以建立只有一个输入时无法完成的电路;
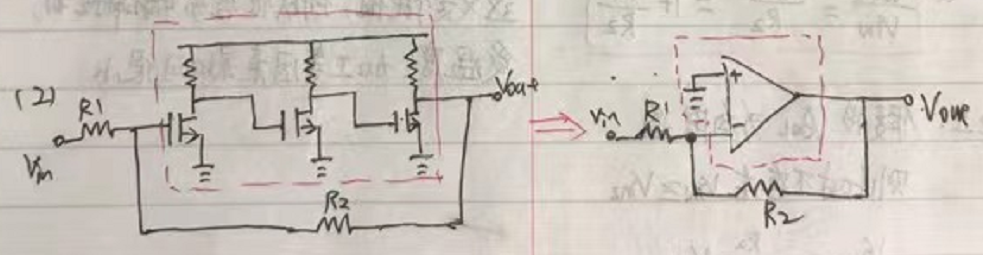
(2) 有时候,若遇到一个复杂系统(比如包括很多晶体管以及级数),将其等效为运放,可以简化分析。
比如说,下图中左侧,觉得这电路,因为反馈电阻R2的存在,顿时觉得复杂。但是如果将三级放大电路等效为运放,那看上去就简单明了了。
我们希望运放是理想的,但是理想丰满,现实总是骨感的。所以实际的运放,总会有很多的不完美。
理想的运放:
开环增益为∞;输入阻抗为∞;输出阻抗为0;带宽为∞。
但实际的运放:
开环增益有限;输入阻抗虽大,但不是∞;输出阻抗虽小,但不是0;带宽有限。
运放的虚短,虚断
因为Vout=Aol*(V+-V-),因为Vout为有限值,而Aol的值很大,那么V+与V-相差很小,即V+~==V-.这就是所谓的虚短。

而因为运算放大器是输入阻抗很高,虽然连线连着,但是电流极小,可以认为为0,即I+=0,I-=0,因此可以认为两个输入与运放是断开的,这就是所谓的虚断。
虚短和虚断这两个概念,在运算电路分析中,是常用的。
运算的基本电路
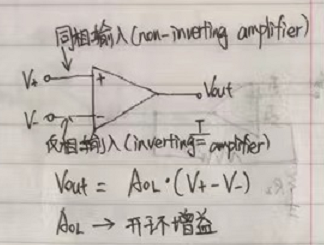
同相放大器(Non-inverting amplifier)

上图中Aol称为开环增益,而Vout/Vin则称为闭环增益。
运算放大器构成的同相放大器,其增益与电阻的比值有关,这个特性优于普通放大器。因为电阻比是能够精确控制的,而且受温度,加工等因素的影响很小。
反相放大器(inverting amplifer)

可以看到,反相放大器的增益仍然是比值,可以精确控制。此时其输入阻抗为R2,与同相放大器相比,输入阻抗变小。而且,如果降低R2以获得更高增益的同时,也降低了输入阻抗。
这在使用反相放大器时,也需要考虑一下。
单位增益缓冲器(Unity-gain buffer)
那单位增益缓冲器又有啥好处呢?也不能放大增益。
如果计算一下单位增益缓冲器的话,你会发现,其输入阻抗接近于无穷大,输出阻抗则接近于0(即使运放本身的输出阻抗不小)。
这使得其可以在不对前级电路产生影响的情况下,感应到前级电路的电压;同时,又能驱动低输入阻抗的电路。
积分器
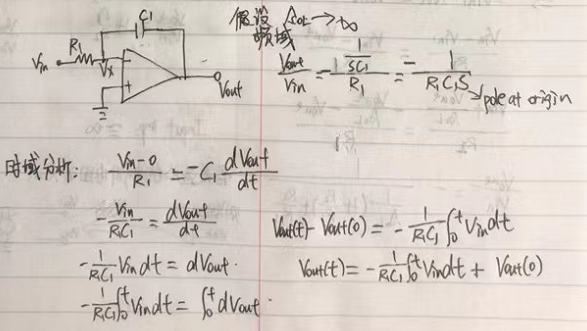

微分器

加法器

精密整流器
简单的二极管整流器有一个问题,就是当输入信号的幅度小于二极管的开启电压VDon时,输出为0,如下图所示。
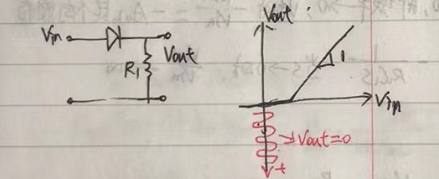
由运放构成的精密整流器,不会存在这样一个问题。

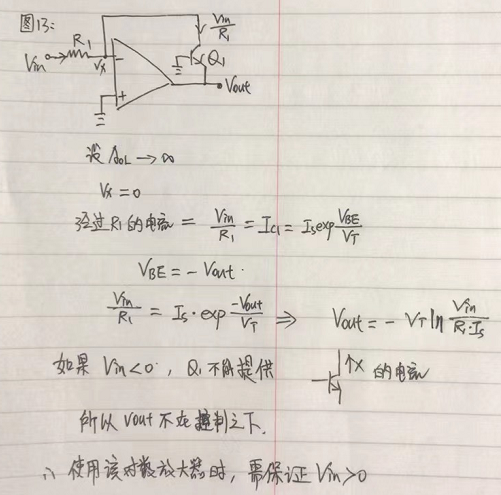
对数放大器
对数放大器的输入输出曲线如下图所示。

如果信号输入幅度较小,则其放大增益大;当信号幅度增加时,其放大增益相应减小。
对数放大器的结构如下图所示。