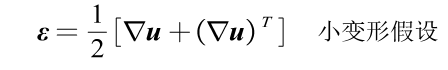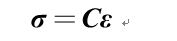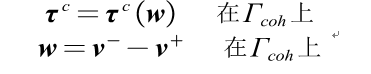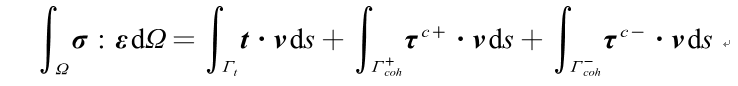浅谈混凝土虚拟裂缝断裂模型
传统的线弹性断裂力学认为裂缝尖端的应力是无穷大(应力奇异性)的,而在实际工程中的材料而言,往往是不切实际的。对于混凝土这种准脆性材料而言,裂缝尖端的塑性区尺寸往往与整个计算区域量度相当,如果在此时还应用线弹性断裂力学的 知识去计算,将大大降低结构实际的裂缝抵抗能力,由此确定的断裂韧度也具有明显的尺寸效应。对于混凝土非线性区域的分析是建立断裂模型的关键环节,本文结合Hillerborg提出的虚拟裂缝模型,简要解释混凝土断裂过程区的非线性行为。
Hillerborg提出一种将断裂力学引入有限元分析的方法,采用假设应力(原文:stresses are assumed)作用于裂缝区域,以下统称黏聚力。断裂力学和有限元方法(FEM)的最新进展使我们有可能分析裂纹扩展。断裂力学给出了裂纹扩展的基本规则,而有限元使这些规则在复杂情况下的应用成为可能。面对复杂的案例,如:裂纹的生成与扩展、两条或多条平行裂纹、弯剪裂纹、收缩应变、混凝土和钢筋的相互作用、水泥浆体和集料的相互作用等,作者从断裂力学的方法中列举了应力强度因子法、能量平衡法、基于Dugdale的strip-yield模型、黏聚力模型。
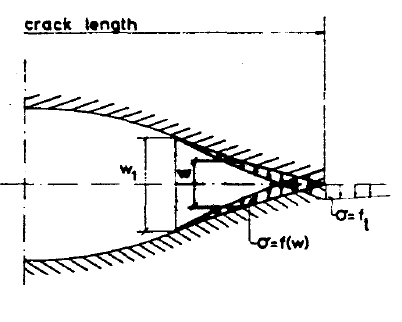
由上图可以看出断裂过程区由两个裂尖确定:虚拟裂尖和实际裂尖,实际裂尖处的黏聚力为0,虚拟裂尖处的应力等于材料抗拉强度。
虚拟裂纹模型将裂纹分解为两部分,即真实自由裂缝部分(完全开裂区)和虚拟裂缝部分(微裂区),自由裂缝表面不传递应力,虚拟裂缝将带状的微裂区简化为一条线裂缝,表面可以传递应力,且应力随着裂缝张开位移的增大而减小。微裂区的存在消除了线弹性断裂力学中裂纹尖端应力的奇异性。对于普通混凝土材料,Hillerborg采用线性软化关系,与拉伸试验结果相当吻合。曲线图如图所示:
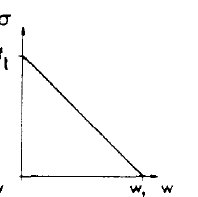
基于能量守恒(断裂过程中产生单位面积新裂纹面所消耗的能量在数值上等于新裂缝面的表面能),软化曲线下的面积即为断裂能。
该模型不仅揭示了新裂纹的扩展,也解释了新裂纹的形成,可以用一个相对粗糙的网格进行,因为没有了应力奇异性,所以对网格密度不是很敏感。
- 混凝土在达到抗拉强度之前是线弹性的(文献中原话是这样的:In the application we further assume that the concrete is linear-elastic until ft is reached.);
当裂缝尖端拉应力达到材料的抗拉极限强度时,假设虚拟裂缝开始扩展;
裂缝扩展过程中,裂缝面上的黏聚应力大小决定于裂缝张开位移。
虚拟裂缝模型的数值实现:虚拟裂缝模型采用分离式裂缝的表征方法,将虚拟裂缝两侧按照分离的几何边界处理,定义裂缝面的软化关系,结合有限元等数值技术来模拟断裂过程区非线性损伤行为。在使用有限元模拟过程中,将裂缝两侧边界通过单元边界来表示,随着裂缝的发展将裂缝边界单元的单节点拆分为双节点,在双节点上设置一对点力,根据软化关系来确定。虚拟裂缝模型的平衡条件(基于《混凝土断裂力学》与《扩展有限元》综合得出):如下图所示的计算域,其边界为。为位移边界,为外载荷边界,为裂纹边界,裂纹的前端是断裂过程区,断裂过程区内有黏聚力。
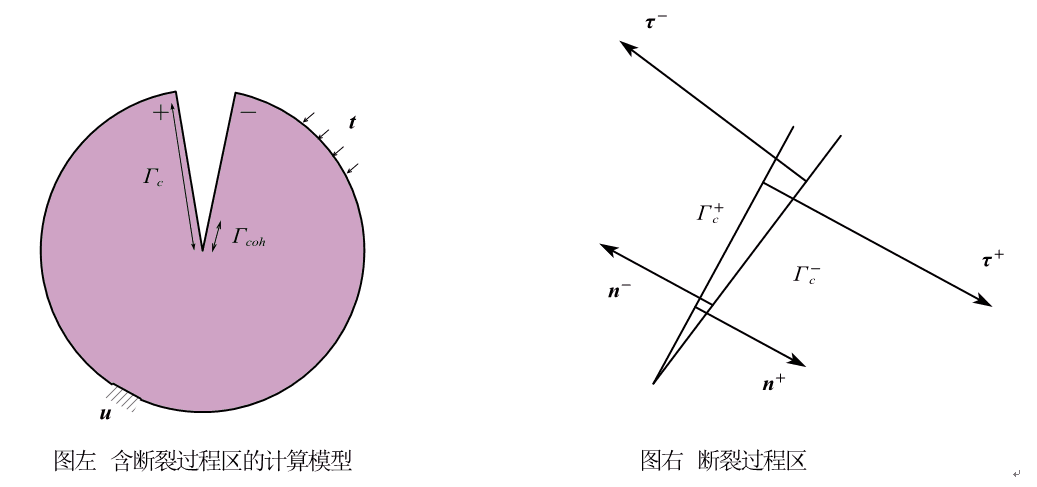

其中:和分别为应力和位移;为边界上外法向单位矢量;为给定位移边界;和为裂纹面上外法向单位矢量;和为裂纹面上黏聚力。
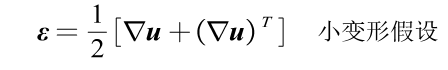
物理方程:
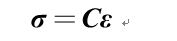
其中,为弹性系数。
黏聚力与裂纹面两侧的相对位移有关,即
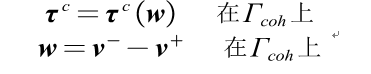
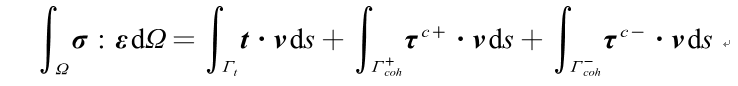
由黏聚力与裂纹面两侧相对位移的关系,可将上式简化为:

以上式子中所用的裂纹面位移皆为法向位移,因为所采用的软化模型均不考虑切向黏聚力的作用,即假定裂纹面的软化特性仅与裂纹面的法向张开量有关。
本文所参考的文献为:Hillerborg A, Modéer M,Petersson P-E. Analysis of crack formation and crack growth in concrete bymeans of fracture mechanics and finite elements. Cement and Concrete Research.1976.
来源:易木木响叮当