弹塑性线性强化切线刚度Umat(2)
今天讨论弹塑性线性强化切线刚度的Umat子程序,与上一节的常刚度法相比,切线刚度就是在常刚度的基础上更新了雅克比行列式,更加适用于非线性较强的情况。
顾名思义,常刚度法就是在计算过程中刚度保持不变,对于非线性较弱的情况模拟结果与真实值误差还可以接受,但对于如断裂、大变形、杂质等非线性较强的情况时,常刚度法的误差往往不能满足实际工程的需要,此时就要试图改变刚度以满足非线性条件。

进入正题
更新雅克比矩阵代码:
C update jacobian matrixw = 9*G**2/(misesEqualStress**2*(H+3*G))do i = 1,NTENSdo j=1,ntensDDSDDE(i,j)=DDSDDE(i,j)-w*deviatoricStress(i)*&deviatoricStress(j)end doend do
其中所涉及到到的理论推导如下:
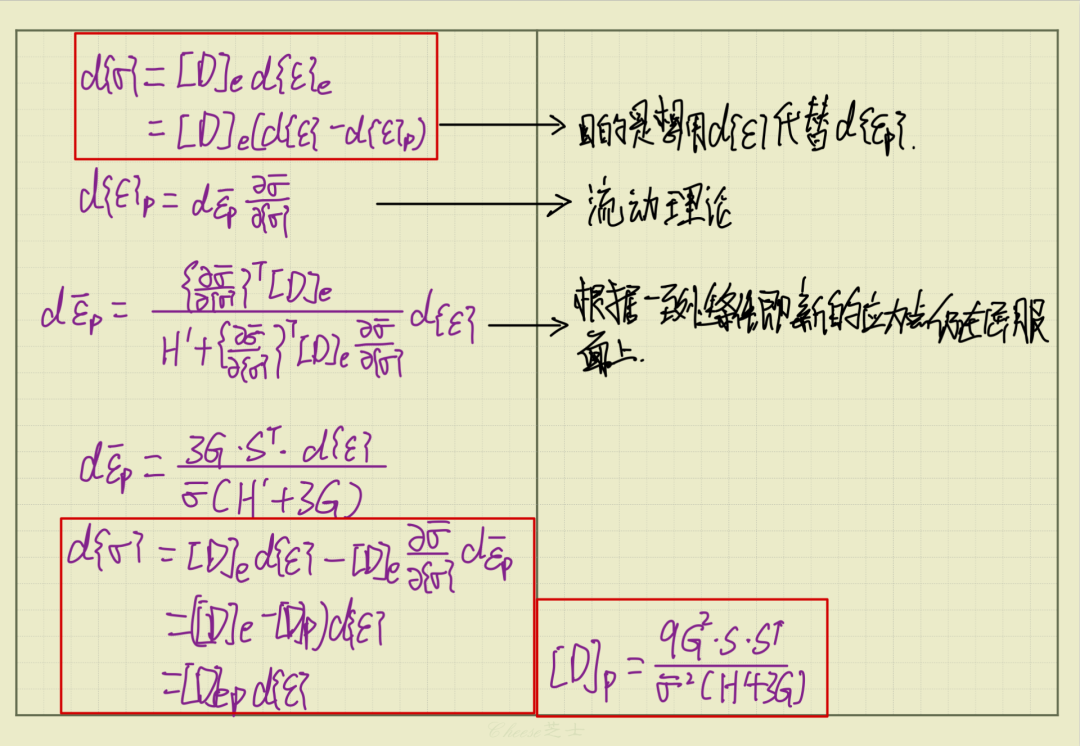 以上公式的主要目的就是想要塑性分析中建立总应变与塑性应变的关系,对雅克比矩阵做了变动,进而用总应变代替塑性应变分析计算。
以上公式的主要目的就是想要塑性分析中建立总应变与塑性应变的关系,对雅克比矩阵做了变动,进而用总应变代替塑性应变分析计算。
从以上理论的推导来看,一致性条件在弹塑性分析中的重要性
还是应用上一节的模型计算结果与常刚度法(中)和Abaqus自带本构(左)做对比:

结果完全一样,此模型非线性行为较弱,所以结果都一致,若是应用于非线性较强的情况,差别就会显示出来,本文为了简化计算,取用的模型较为简单,读者若有兴趣,可在自己模型中应用,验证三者的效果。
最后引用陈老(陈惠发)在他书中的一段话,用于阐述塑形理论框架的核心内容:
(加载准则)所发生的的变形类型,特别是必须判断发生的是纯弹性变形还是弹塑性变形;
(流动法则)若是后者,必须确定塑性应变的正负符号;
(强化法则)对于强化响应,必须补充一个弹性范围的估计方法;
(强化参数)必须记录塑性变形历史,因为塑性变形导致弹性范围的改变;
(相容条件)此外,在弹性分析中,必须强调处于弹性范围边界的应力状态条件。
来源:易木木响叮当
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-05-31
最近编辑:1年前
还没有评论
相关推荐
最新文章
热门文章


