首页/文章/ 详情

Matlab有限元基础编程 | 3节点杆单元(附云图绘制)

易木木响叮当

1年前浏览3730

今天给大家分享的主要内容：三节点杆单元Matlab有限元编程，并附带云图绘制后处理程序，获取方法，见文末。

前些日子，木木在学习有限元的过程中，在有限元领域发现一位博主@SAGARBODKHE,他主要也是更新有限元编程的一些视频，发现他有一个三节点杆单元的程序，觉得有趣就分享出来，希望能加深大家对有限元基础编程的理解。

理论基础

对比二节点杆单元

三节点杆单元二节点杆单元在单元节点顺序上的区别是，前者在单元的中心增加一个节点，节点顺序为：1、3、2。

在位移插值阶次的区别是，前者的位移插值函数使用的是二次抛物线插值，相比于两节点杆单元的线性位移插值函数。精度更高，可使用较少单元，满足精度要求。

题外话：

研究生数值分析教材一般先将误差分析，然后就是插值拟合，在学习插值方法时，也是先讲线性插值，然后二次、牛顿等等，在最初学习阶段，只知插值函数阶次在一定条件下，阶次越高，精度越好。

有限元方法与数值分析思想密切相关，仔细琢磨一下就可联想到位移插值形函数与数值分析中拉格朗日插值等思想一致，当然还有许多方面也都密切相关。

位移模式

单元刚度

单元刚度矩阵的推导就不在这里赘述，前人已经通过各种方法推导得出刚度矩阵，这里将推导完成的刚度矩阵展示如下：

其中，为单元长度。

在杆单元的编程中，刚度矩阵不需数值积分方法求得近似解，直接用现成的即可！

数值实现

本次的程序没有设置函数文件，直接是一套主程序，运行即可，也可设置断点，看每一步如何运行，加上云图绘制语句共100行左右（包含注释、空行），行数较少，可以尝试去掌握它。

模型描述

位移求解

有限元程序主要有两部分组成，位移求解、应力等其他分量求解及云图绘制。

个人观点：因为目前所采用的思想主要是以节点位移为未知量的有限元求解，故其他分量都是建立在求得节点位移的基础上展开的，以及后续的云图绘制。

虽然云图绘制并不是必须的，但是效果上很棒，值得学习（虽然我不会），但是对已有的绘图语句会用即可！

Matlab 程序

L=1;
A=1;
E=100e9;
nel=20;

nnp=2*nel+1;
K=zeros(nnp,nnp);
F=zeros(nnp,1);
Lel = L/nel;

%% Stifness Matrix Generation
for i=1:nel
    range=[ 2*i-1 2*i 2*i+1];
    K(range,range)= K(range,range) + (A*E)/(3*Lel)*[7 -8 1;-8 16 -8;1 -8 7];
end

%% Boundary Conditions

fixed_nodes = [1];
free_nodes = setxor(1:nnp,fixed_nodes);%setxor集合运算符（异或）

force_nodes =[nnp];
force_val =[ 1000];
F(force_nodes)= force_val;
%% Partitioning K and F matrix

Kpart = K(free_nodes,free_nodes);
Fpart = F(free_nodes,1);

%% Solve the system of eqn

Up = Kpart\Fpart;
U=zeros(nnp,1);
U(free_nodes)=Up;

在以上程序中需要注意的地方：

nnp=2*nel+1该语句中声明了节点自由度数目的大小，大家在套用到2节点程序时，需要将此改为nnp=nel+1;
在形成总刚时，使用的编程思路和之前我所分享的思路不同，不过我觉得他的这个思路挺方便的，不用另外写整体刚度的组装子函数，大家感兴趣可以将该思路与之前我们所采用的整体刚度组装子程序验证一下，完全正确；
free_nodes = setxor(1:nnp,fixed_nodes)使用到了matlab中setxor集合运算符（异或），两个集合排除掉中间空白区域。

其余的编程思路与之前分享推文中的编程思路相同，不加赘述。

位移曲线绘制

%% Visualization
X=zeros(nnp,1);
Y=zeros(nnp,1);

for i=2:nnp
    X(i)=X(i-1) + Lel;
end

Xdef=X+U;
Ydef=Y;
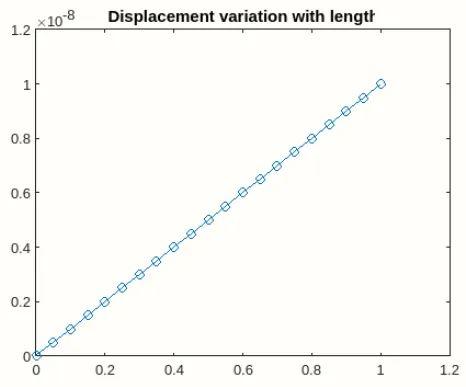
 plot(X,U,'-o')
 title('Displacement variation with length')

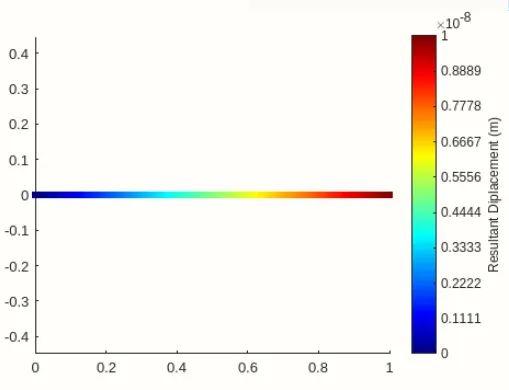
云图绘制

Xdef(end+1)=NaN;
Ydef(end+1)=NaN;
c=U;
c(end+1)=0;

patch(Xdef,Ydef,c,'EdgeColor','interp','Linewidth',5);

colormap jet;
cb = colorbar;
t=get(cb,'Limits');
set(cb,'Ticks',linspace(t(1),t(2),10))
cb.Label.String = 'Resultant Diplacement (m)';
axis equal

xP=zeros(2*nnp,1);
yP=zeros(2*nnp,1);
cP=zeros(2*nnp,1);
h=0.05;
for j=1:2:2*nnp
    xP(j)=Xdef((j+1)/2);
    xP(j+1)=xP(j);
    yP(j)=0+h;
    yP(j+1)=0-h;
    cP(j)=U((j+1)/2);
    cP(j+1)=cP(j);
end

xF=zeros(4,2*nel);
yF=zeros(4,2*nel);
cF=zeros(4,2*nel);
for j=1:2*nel

    xcur=xP((2*j)-1:(2*j)+2);
    ycur=yP((2*j)-1:(2*j)+2);
    ccur=cP((2*j)-1:(2*j)+2);

    xF(:,j)=xcur([1 3 4 2]);
    yF(:,j)=ycur([1 3 4 2]);
    cF(:,j)=ccur([1 3 4 2]);
end

patch(xF,yF,cF)

colormap jet;
cb = colorbar;
t=get(cb,'Limits');
set(cb,'Ticks',linspace(t(1),t(2),10))
cb.Label.String = 'Resultant Diplacement (m)';
axis equal