非线性有限元编程 | 接触（2）

本篇推文延续上一节的接触非线性内容，继续深入了解接触问题，主要做了下摩擦相关的内容，主要方面如下：

1. 使用理论解析方法求出摩擦力及滑动位移；
2. 基于拉格朗日乘子法求摩擦力及滑动位移；
3. 基于罚函数法求摩擦力及滑动位移；

问题描述

考虑受均布荷载作用的悬臂梁，梁的自由端受刚性块的限制，如下图所示，梁的末端与刚性块之间存在一个小间隙。均布荷载    =1 kN/m，梁长    =1 m，抗弯刚度EI=    N    ，初始间隙    =1 mm。梁右端承受水平力    ，轴向刚度    N，摩擦系数    。

 

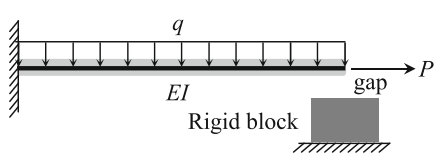
假设不存在摩擦

由上一节的接触知识可知，在均布荷载作用下，刚块会产生75N的接触力，假设不存在摩擦的情况，我们看一下梁端在水平荷载作用下移动多少？

存在摩擦情况

当界面存在摩擦力时，下图所示，梁端接触到刚体块时，可能会发生滑动，也可能不会，类似于上一节的解释，将是否滑动的条件也罗列为一种约束条件：

 

第1、2个公式描述了梁端在发生接触时，是否发生滑动摩擦的条件，    为接触力（75N），    为产生的摩擦力。在第三个公式（连续性条件）时，可将滑动位移量    视为拉格朗日乘子，摩擦力公式    作为约束条件。

解析法

若不发生滑动，即    ：

即    ，与第1个公式(    )相违背，故判断出梁在与刚块接触后，发生了滑动摩擦。

于是带进第二个公式（），得出    ，滑移量    可写为    。

拉格朗日乘子法

在使用拉格朗日乘子法中，可使用连续性条件(    )作为约束条件，将滑动位移量    视为拉格朗日乘子。结合滑移量公式(    )，可得出摩擦力公式：

根据连续性条件可得：

可以得到两个解：    ，    。    的情况在解析法中已经讨论过；得出    ，根据滑动摩擦条件：，得出摩擦力    =37.5N。

罚函数法

在罚函数法中，允许，类似于上篇推文里讲到的，加入一个罚系数，使得多出的量与罚系数成正比。基于罚函数定义的摩擦力(类似于侵入量)公式可表示为：

当    时，    ；当时，    。滑移量可表示为    ，    为罚系数，结合上式与摩擦力公式（    ），得出滑移量公式：

罚系数分别去不同的值，代入上式，得到的滑移量和摩擦力将收敛于解析解，如下表所示：

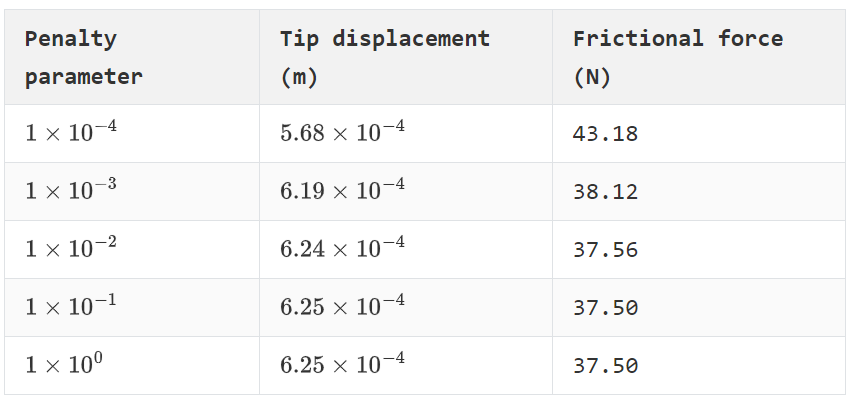
大家有没有注意到以上所取得罚系数相对于上一篇中得罚系数很小，这是什么原因呢？留给读者自行思考，可以在留言区发表看法哦~

最终梁端的滑移量收敛于0.625mm，摩擦力收敛于37.5N。

如果你有合适的有限元开发类的工作推荐，欢迎联系木木！！！