使用分子动力学轨迹来预测大型自旋系统中的核自旋弛豫行为

1年前浏览13675

1. 导读

分子动力学（MD）模拟对于研究小分子和大型生物分子系统的构象移动性非常有用，但对于MD力场预测的构象能量和分布的准确性仍存在疑虑。有令人鼓舞的迹象表明，MD可以合理预测构象之间的转变时间尺度，但这一成功必须得到验证：除了少数例外，力场参数通常设定为重现热力学性质和量子力学能量，而不是构象转变的速率或停留时间。随着开发出具有正确自扩散和粘度的新水模型，以及探索对蛋白质非结构区域建模的新方法，彻底的实验验证变得越来越重要。

磁共振在探测构象及其动态特性方面具有独特的能力，尤其通过自旋弛豫和交叉弛豫测量。然而，大多数用于解释自旋弛豫数据的模型在局部移动性方面做出了简化的近似，并使用了孤立自旋对模型。最近出现了更为复杂的利用MD模拟进行NMR和EPR弛豫的方法，但它们仍然主要使用自旋对近似；我们小组的工作也属于这个类别。需要的是一个软件框架，能够将MD轨迹直接转换为任意自旋系统的弛豫超算符。

鉴于此，本文报告了在Spinach库中实现了这个功能。我们在使用OPC和TIP5P水的甘露糖（GLYCAM06力场）上测试了所提出的方法。甘露糖的构象动力学已经有了较好的研究，尤其是通过使用孤立自旋对近似解释的13C自旋弛豫测量。在这里，我们将重点放在1H-1H核Overhauser效应（NOE）上，这种效应探测葡萄糖的H1环异构体质子（图1）和连接葡萄糖和果糖残基的糖苷键两侧的果糖H11，12质子之间的接触。我们证明，从1微秒长的MD轨迹中提取的（交叉）弛豫率与实验数据非常吻合，考虑到NOE差异为9-25%，这会转化为1.5-4.2%的距离误差。这对于GLYCAM06力场以及OPC和TIP5P水模型来说是一个好消息。核自旋（交叉）弛豫率很容易测量，我们建议将这样的测试纳入新型分子动力学力场的标准基准测试集中。相关工作以“Using molecular dynamics trajectories to predict nuclear spin relaxation behaviour in large spin systems”发表在《Journal of Magnetic Resonance》上。

2. 图文速递

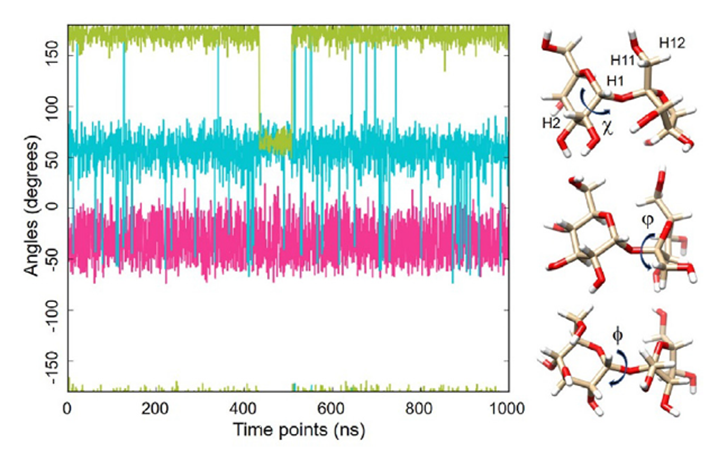
图1. 甘露糖内所示二面角的动力学特性（1毫秒MD轨迹，GLYCAM06甘露糖，OPC水，300K）。v（H2-C2-C1-O20）以绿色显示，u（C1-O20-C2-C1）以青色显示，/（H1-C1-O20-C2）以红色显示。

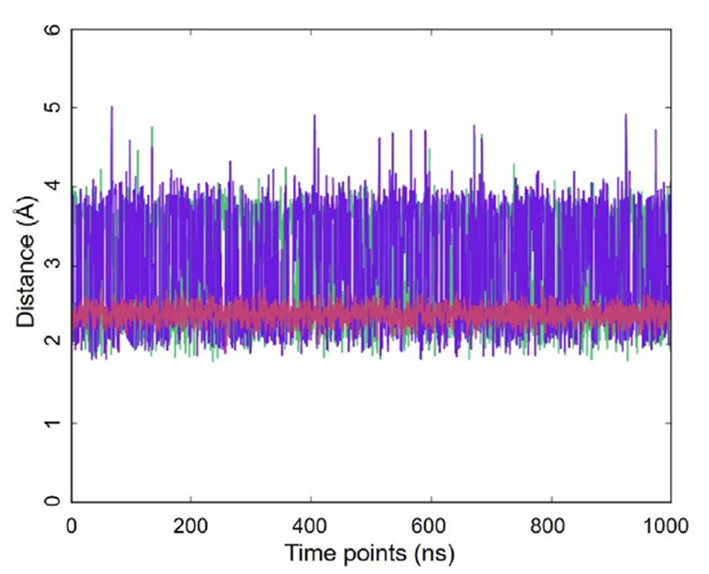
图2. 原子之间的距离动态（1毫秒MD轨迹，GLYCAM06甘露糖，OPC水，300K）：葡萄糖H1到果糖H11的距离（绿色），葡萄糖H1到果糖H12的距离（紫色），葡萄糖H1到葡萄糖H2的距离（红色）。

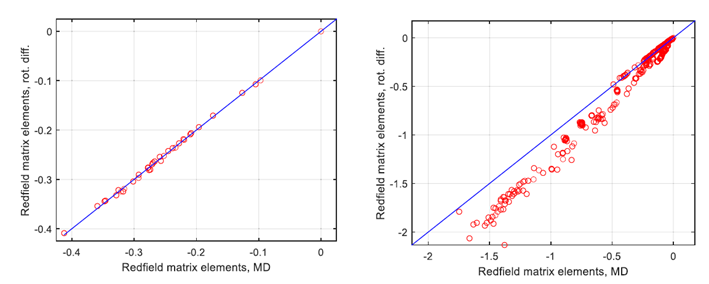
图3. 对比分析处理（使用纯旋转扩散近似）和数值处理（使用MD轨迹积分，OPC水）中弛豫超算符的非零元素之间的差异，随着内部运动对自旋弛豫的贡献增加。左侧面板：相对刚性的葡萄糖环中的3个自旋子系统（H1，H2，H4），其中偶极耦合调制几乎完全是旋转性质。（右侧面板）包含6个自旋子系统（葡萄糖的H1，H2，H3，H5；果糖的H11，H12），其中存在与糖苷键和外环C1-C2果糖键相关的显著内部运动。两个面板中的蓝线对应旋转相关时间为78皮秒，该值是通过拟合左侧面板的数据获得的。

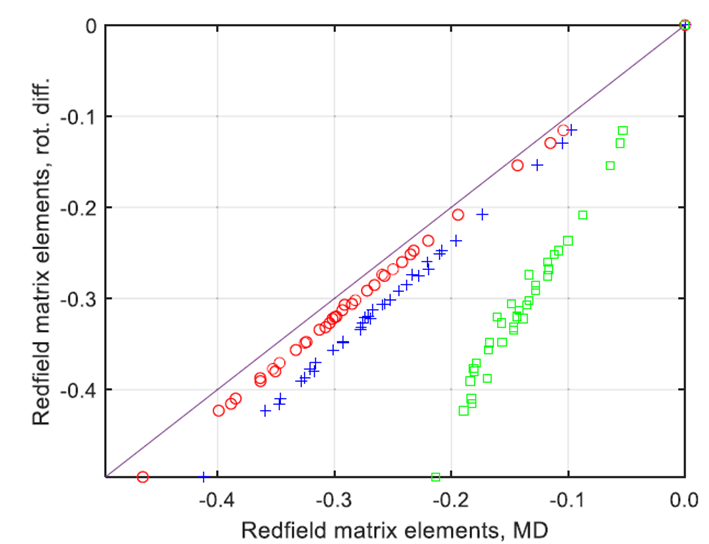
图4.. 来自TIP3P水（绿色方块）、TIP5P水（红色圆圈）和OPC水（蓝色十字）的分子动力学轨迹所得到的Redfield弛豫超算符的非零元素（X轴），与使用纯旋转扩散近似和旋转相关时间为100皮秒获得的相应元素的解析弛豫超算符进行对比（绿色方块代表TIP3P，红色圆圈代表TIP5P，蓝色十字代表OPC）。

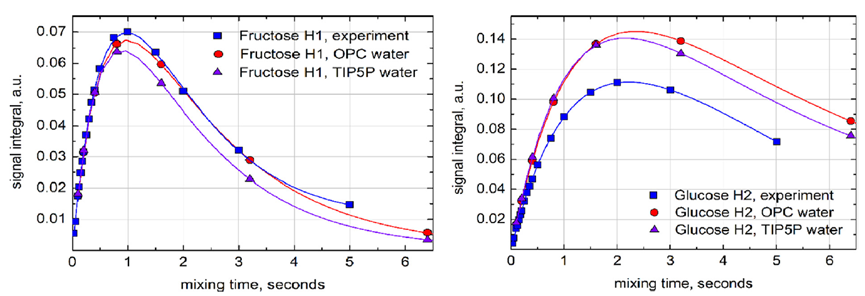
图5. 在葡萄糖H1质子自旋反转后，实验（蓝色）和模拟（OPC水为红色，TIP5P水为紫色）的核Overhauser效应（NOE）累积曲线的比较（曲线为双指数拟合）。模拟使用以葡萄糖H1为中心的8个自旋系统进行，包括（Glc H1-H5；Fruc H11，H12，H3）。信号积分是反转共振强度的分数。实验数据在600 MHz和308 K下收集；选择更高的温度是为了补偿D₂O的增加粘度。没有尝试补偿蔗糖浓度对粘度的影响 - 预计该影响在0.5%以下。在进行核磁共振实验之前，样品被除气处理。

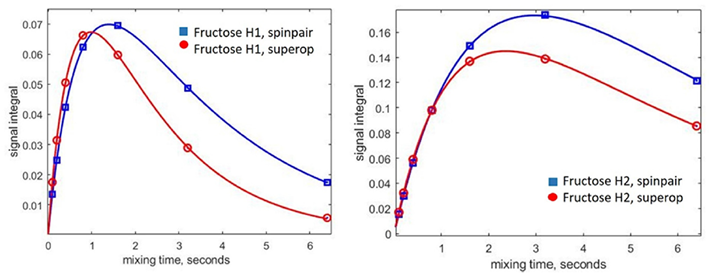
图6. 使用自旋对（蓝色）和完整自旋系统（红色）方法对模拟的核Overhauser效应（NOE）累积曲线进行比较（在葡萄糖H1共振反转时）。实线是双指数拟合。左侧面板：果糖H11 + H12质子。右侧面板：葡萄糖H2质子。

3. 小结

我们提出了一个新工具，用于将实验自旋弛豫数据与基于分子动力学轨迹的模拟进行比较。它通过对Redfield积分进行数值评估直接计算自旋弛豫超算符。该工具已集成到Spinach软件包中，并能够模拟多种自旋弛豫实验，包括具有显著强耦合和弛豫干涉效应的自旋系统。这类计算直到最近才变得可行，其中有五个主要因素起到了贡献：（a）具备足够处理能力的图形卡的易得性（NVidia Ampere架构超过10TFLOPS的处理能力，约等于2002年全球最大超级计算机）；（b）在磁共振中开发和实施了用于弛豫超算符和稀疏矩阵指数的大规模方法；（c）Matlab的性能和语法灵活性不断提高，其中的程序代码通常比用人类语言和标准数学符号描述更短且更易读；（d）出现了线性复杂度缩放的液态自旋动力学模拟方法，使得蛋白质大小的系统不再无法达到；（e）提供了足够长的分子动力学轨迹，以同时在方程（3）中对上限和集平均值进行收敛。

我们通过在蔗糖上模拟NOE实验对该工具进行了测试，使用了GLYCAM06力场下的1毫秒分子动力学轨迹和OPC、TIP5P和TIP3P水模型。与实验的一致性非常好，考虑到0-25%的NOE初始斜率的差异对应刚性结构中的距离误差为0-4.2%。这对于GLYCAM06糖类参数化和OPC、TIP5P水模型来说是非常好的，但TIP3P效果不佳。上述模拟的CPU时间需求不超过运行分子动力学轨迹所需的时间。一旦计算了弛豫超算符，通过计算多个混合时间下的NOE或模拟任何其他弛豫实验所消耗的CPU时间是微不足道的。在具有24个CPU核心的系统中，使用IK-0（3）基组和每2皮秒采样一次的1皮秒轨迹，8自旋弛豫超算符计算大约需要30小时；如果使用GPU，这个时间将大大缩短。预计更大的自旋系统将变得简单：一旦自旋数超过受限态空间近似中的强相互作用团簇的大小（通常在液态NMR模拟中少于五个自旋），计算复杂性与自旋系统的大小大约呈线性关系。

一个用于预测混凝土拉伸强度的多尺度有限元模型

一个用于预测混凝土拉伸强度的多尺度有限元模型1.导读混凝土和其他水泥基材料是结构工程中最常用的材料。在大多数结构设计和研究中，混凝土通常被视为均质材料。但事实上，混凝土是一种异质复合材料。例如普通混凝土由水、粗骨料、细骨料和水泥组成，这些材料混合形成能够承受载荷的系统。混凝土是典型的准脆性材料，其在使用过程中的破坏通常始于初始微裂缝，然后发展成为宏观裂缝。一旦形成宏观裂缝，裂缝会迅速穿透混凝土，然后混凝土破坏。混凝土的性能具有一定的随机性，这也与混凝土在多个尺度上的异质组成有关。因此，为了更好地理解混凝土的机理并支持混凝土材料和结构的设计，需要研究混凝土在多个尺度上的行为。多尺度方法是研究复合材料力学特性的强有力工具。多尺度方法分为两类：并发和分层。并发方法的特点是在同一结构中同时计算不同尺度的两个域，使用耦合方法，如网格分裂技术。而分层方法则在不同尺度上计算模型，并在它们之间转换力学信息。均质化方法通过在微观代表体（RVE)上应用宏观控制方程（周期共同方程，本构方程等)来捕获有效的宏观特性。对于均质化方法，信息传递是单向的，即从小尺度到大尺度。当均质化方法嵌套在有限元（FE)框架中，采用耦合方法连接不同尺度模型，以在它们之间转换信息时，也被称为FE2方法。嵌套FE2的特点是在粗粒度模型中不需要描述现象学本构模型。然而，FE2方法需要在每次迭代时在尺度之间更新信息，因此计算成本很高。随着计算机技术的发展，采取并行计算和数据驱动等措施来提高FE2方法的计算效率。多尺度方法在混凝土材料中的应用也逐渐增加。特别是近年来，混凝土中介观尺度模型已成为研究热点。许多介观尺度建模方法已经被开发并用于研究介观组成对混凝土力学行为的影响。然而，仅仅依靠介观尺度模型就难以基于其组成预测混凝土的力学行为，因为在介观尺度模型中不能很好地考虑除粗集料以外的组成材料（水泥、细集料)。尽管一些研究者已经将砂浆基体的强度等级作为介观尺度模型中的因素，但它仍然无法实现基于组成预测力学行为的目标。因此，为了解决这个问题，需要进行更低尺度的考虑。鉴于此，广西大学余鹏等人提出了一种用于预测混凝土拉伸强度的三维多尺度模型。通过使用Python程序，HYMOSTURC生成水化水泥糊（HCP）的微观结构，并导出到Abaqus中。使用局部背景网格法直接生成砂浆和混凝土的中尺度模型。采用一个非耦合多尺度方法将参数从小尺度转移到大尺度模型。在尺度重叠的情况下，通过一个简化的非耦合平均法进行参数传递。最后，通过砂浆的弯曲测试和混凝土的拉伸分裂试验验证了多尺度模型。相关工作以“Amultiscalefiniteelementmodelforpredictionoftensilestrengthofconcrete”发表在《FiniteElementsinAnalysis&Design》上。2.图文速递图1.混凝土在不同尺度下的结构和形态。图2上图显示了用于有限元模型重建的图像重建过程，包括计算机断层扫描（CT）扫描和数字图像处理。中图展示了不同水灰比（w/c）下的水化硅酸盐（HCP）有限元模型，包括微观尺度模型。下图显示了HCP单轴加载的响应，包括应力-应变曲线和破坏模式。图3.不同水灰比的HCP试件的应力-应变曲线。图4.砂浆介观尺度有限元模型。图5.上图为不同水胶比下砂浆试样的应力-应变曲线。中图为不同水灰比的砂浆在单轴拉伸下的破坏模式。下图是不同水灰比的砂浆试件在峰值后的应力-位移曲线。图6.混凝土的介观尺度有限元模型。图7.具有不同ITZ性质和不同水灰比的混凝土破坏模式。图8.不同水灰比混凝土在劈裂拉伸下的破坏模式。图9.实验和模拟的破坏模式比较3.小结本文提出了一个多尺度有限元模型，包括微观尺度的高性能混凝土（HCP）模型、中观尺度的砂浆模型和混凝土的中观尺度模型，用于描述混凝土的力学性能。研究了三组不同水灰比（w/c）的混凝土。HCP的微观结构是通过水化模拟软件HYMOSTRUC3D生成，并导入到有限元软件Abaqus中进行拉伸模拟。通过施加循环荷载，获得了单轴拉伸的应力应变曲线和后峰值的应力应变关系及损伤变量。将损伤变量、应力和应变关系进行拟合，得到了HCP的拉伸性能参数，作为砂浆中观尺度模型的输入参数。中观尺度砂浆模型是通过局部背景网格法建立的，模型的集料含量和级配符合实际。通过拉伸模拟获得的应力应变曲线后峰值行为非常脆性。由于尺度重叠问题，采用了解耦平均方法获得破损区域的后峰值应力位移曲线，并通过砂浆均匀模型的验证。通过砂浆的数值折弯试验，初步验证了所提出的多尺度模型，模拟结果与实验结果吻合。中观尺度的混凝土有限元模型建立用于模拟混凝土的劈裂拉伸行为。随着界面过渡区（ITZ）机械性能的提高和w/c比的降低，混凝土中裂纹路径变得更加复杂，裂纹倾向于穿过骨料。对于普通强度的混凝土，优化ITZ的机械性能和降低w/c比是提高劈裂拉伸强度的有效方法。对于高强混凝土，应使用高强骨料以增强裂纹路径复杂性，从而提高混凝土强度。所提出的多尺度模型可以更好地预测混凝土的劈裂拉伸行为，特别是位移响应，基于混凝土的组成。该多尺度框架也可应用于其他水泥基材料的研究。

有附件