电流放大倍数β、截止频率fβ,特征频率fT三者间的关系,巨详细!
上上周发的文章《三极管的频率问题+文末送书福利》(点击,可以直接访问),送的书是都已经送出了,但文末提出的三个问题中的第一个问题“本文的分析逻辑是否存在问题?”,没有小伙伴指出本文分析逻辑相关问题。
那到底有没有问题呢?我心里一直存在疑虑。

到底有没有问题?
经过这段时间的研究,结论是:有问题,而且是概念上的混淆!

哪里有问题?
关于特征频率概念的解释,自然是没有问题。
在接下来输入信号频率为100MHz、200MHz和300MHz时,拿输出信号波形与输入信号波形做对比。100MHz对应的电压放大倍数为A,200MHz对应B,300MHz对应C,并得出A>B>C≈1。
这里出现问题了。
这里面需要说明,我们说的特征频率fT是针对电流放大倍数β而言,不是针对电路的电压放大倍数。在频率近似等于特征频率fT时,是三极管的电流放大倍数为1,这并不能说明电压放大倍数为1。这里是把电流放大倍数β和电压放大倍数Av混淆了。
应该是怎样的呢?请继续往下看。

电流放大倍数β
电压放大倍数Av,是放大电路输出信号与输入信号的幅值比例关系 ,这个比较直观。那电流放大倍数β呢,这里专指是共射极放大电路,Ic与Ib的幅值关系。
在三极管的通频带内,忽略耦合电容、旁路电容以及三极管的结电容、PCB走线的分布电容之后,我们可以有H参数小信号模型,如下图所示。此时的β更多是温度有关,不过多考虑与频率的关系(实际是有关系的)。

但是在《三极管的频率问题+文末送书福利》中,100M~300MHz可能已经超出三极管的通频带,这里就不能再忽略三极管的结电容,H参数小信号模型也不再适用。此时需要考虑使用适合高频的混合π高频小信号模型。
β在混合π高频小信号模型下的关系式是怎样的呢?我把整个推导验算过程放上,下面在逐步分析。
说明:以下板书推导为硬件微讲堂号主手写,咱杜绝搬运网上的图片。

①三极管,明确b、e、c极;(第一步是来打酱油的

 )
)
②需要考虑下三极管的体电阻(rbb'/re/rc)和结电阻(rb'c/rb'e);
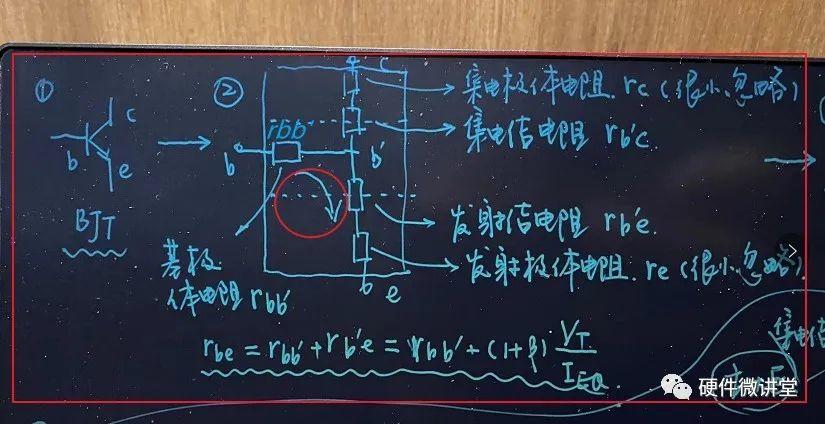
这里有两个关系式,需要了解。rb'e是发射结正偏电阻折算到基极回路(如上图红色圆圈)的等效电阻。rbe是三极管基极和发射极之间的电阻。
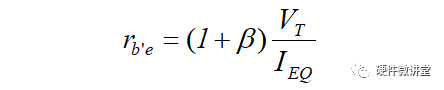

③在高频模式下,还需要考虑三极管的结电容Cb'c/Cb'e,另外还有受控电流源和集电极-发射极之间的电阻rce。注意此时由于结电容的影响,受控电流源不再完全受基极电流Ib控制,不能再用βxIb来表示(β也是频率的函数),需要用gm*Vb'e表示。gm是跨导,受控电流源受控于发射结上的电压Vb'e。

由于三极管处于放大状态,此时的发射结正偏,集电结反偏。集电结反向截止,rb'c和rce会很大,因此可以理解为开路。于是就有了第4步。
④将rb'c和rce拿掉后,就有了三极管的混合π高频小信号模型,如下图所示。

这里的Cb'e很好理解,可以把它当做和rb'e并联的阻抗。Cb'c则跨接在输入回路和输出回路,不太好处理。
⑤既然是高频模型,此时我们讨论的β就是交流电流放大倍数。而分析共射组态的交流电流放大倍数是有一个前提的:

Vce=常数,即为c-e之间电位没有变化量。对于交流通路而言,等效为c-e短路。这点对于概念的理解,很重要!
在混合π高频模型下,c极和e极短路,则Cb'c原本跨接在b-c之间,可以等效为跨接在b-e之间。于是,模型可以进一步简化,如下图所示:

Cb'e和Cb'c一起和rb'e并联,这样一来,计算Ib就很方便了。
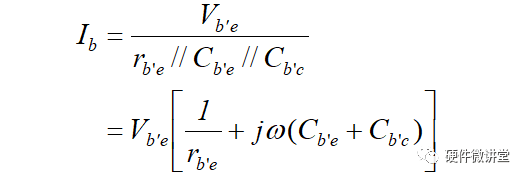
而Ic的计算就很简单了,Ic=gm*Vb'e。
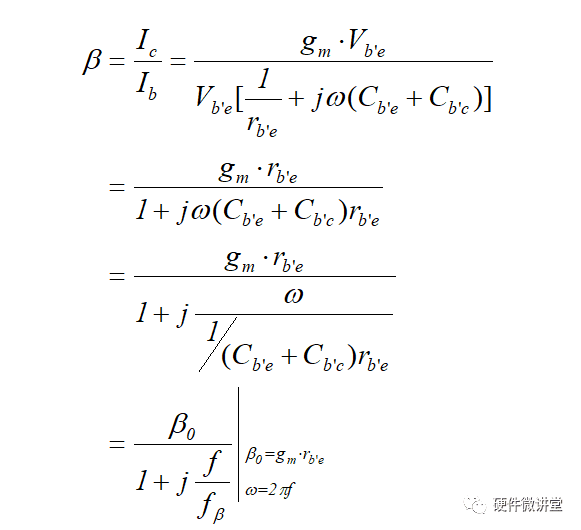
注意:β0就是低频情况下的电流放大倍数,在器件规格书中给出的β就是这里的β0。
而为什么β0=gm*rb'e?这里也是可以推导的,但今天在这里不做展开。
从上述推导过程可以看出,β是频率f的函数,其数值随频率变化,而且影响不能被忽略。这里也解释了为什么在高频模式下,受控电流源不能继续使用β*Ib来表示。
另外,这个关系式存在一阶极点,当f=fβ,β的幅频特性出现拐点。
那fβ=?请继续往下看。

共射截止频率fβ

上图中的fβ就是共射组态的截止频率。

当f<<fβ时,|β|=β0;
当f=fβ时,|β|=β0/√2=0.707*β0,即-3dB转折点;
当f>>fβ时,|β|=β0*fβ/f,即:|β|*f=β0*fβ;


特征频率fT
当|β|=1时,f=β0*fβ,此时的f就是fT,特征频率。
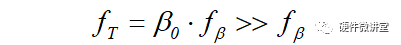
这里也可以看出特征频率fT与截止频率的关系:fT是截止频率fβ的β0倍,是远大于fβ。

总结
今天讨论的内容先到这里,简单总结下讨论的内容:
怎么样?一个简短的问题,给出的回答可浅可深。我的助攻只能到这里,能否晋升到陆地神仙境,一剑开天门,就看你的造化了!




