微元体!最诡异的力学模型
微元体模型,在力学分析中非常常见,非常基本,也非常重要。学过力学的人肯定都知道这个力学模型。不知道读者有没有感受到,微元体模型其实是非常诡异的模型。或者力学老师在授课的时候,有没有提过这个观点。
诡异之处在于:需要微元体是个点的时候,它“嗖”的一下变成点了,需要它变成体的时候,它“嗖”的一下就变成体了。亦点亦体!诡异不?你困惑不?
你常见的微元体可能是这样的!
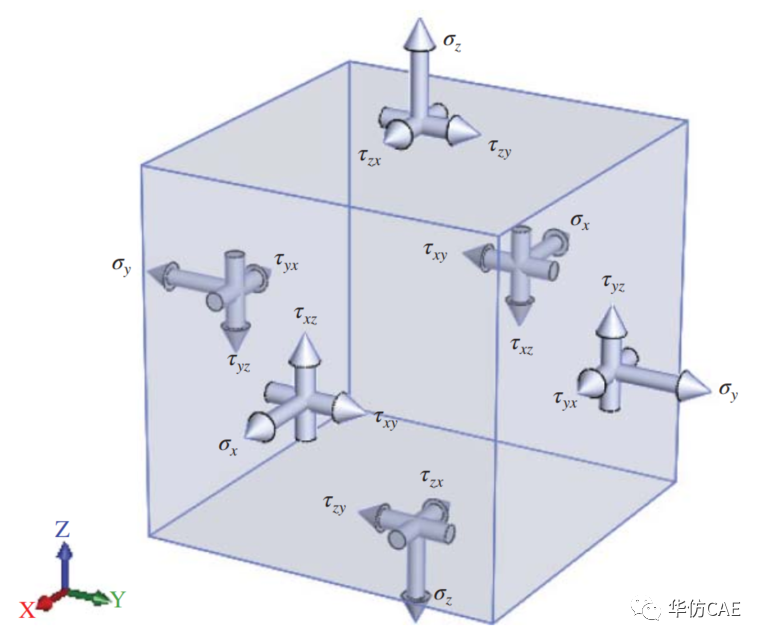 三维微元体 | 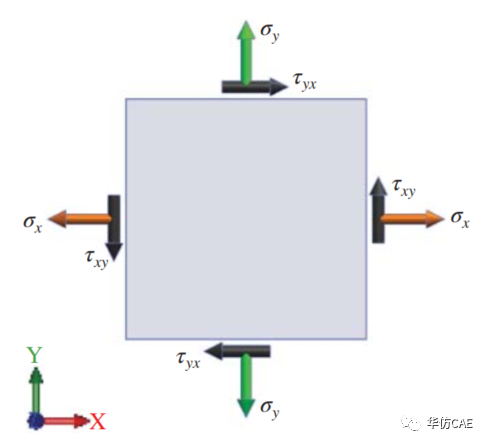 二维微元体 |
但是,微元体其实还可能是这样的!
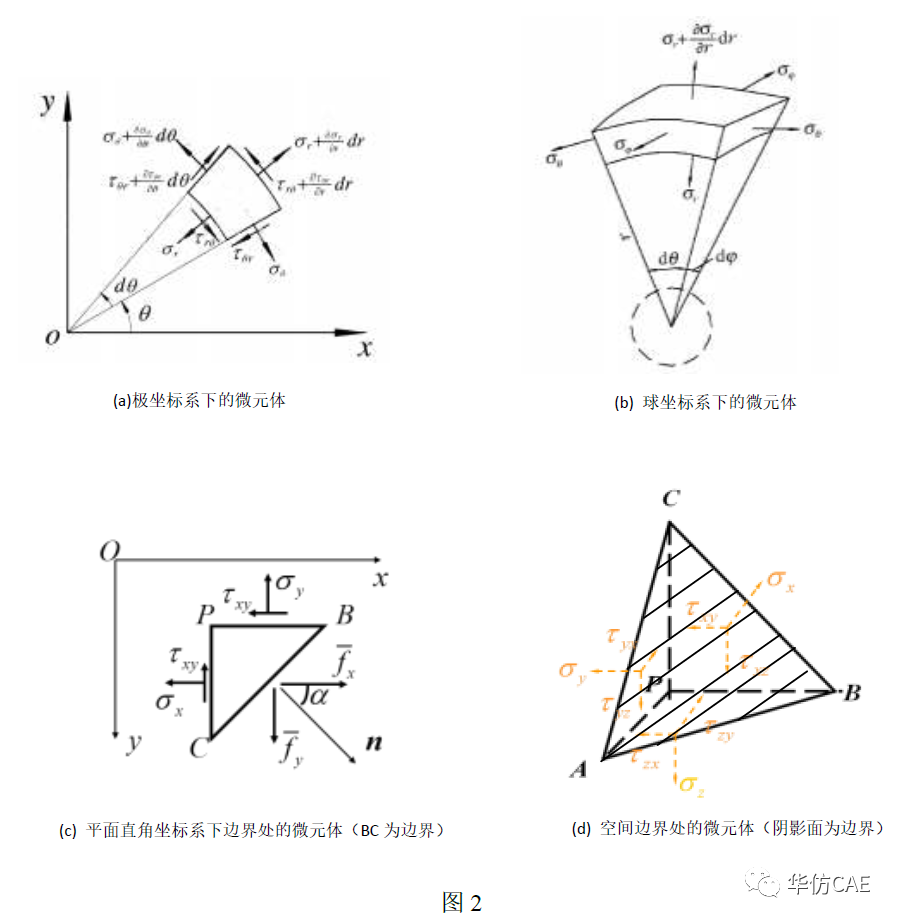
微元体的形状并不固定。直角坐标系下,可以用六面体作为微元体;如果在极坐标下,我们又见到了环形一部分的微元体;球坐标系下,又变成了球冠的一部分。平面直接坐标系下的微元体还可能是三角形,空间问题微元体又可以取为四面体。微元体的具体取法通常会因具体问题而变,远不止上面罗列的几种情况。
所以微元体不仅亦点亦体,而且形状多变,诡异不?你困惑不?
无穷小量是微积分理论中的重要概念。
微元体属于无穷小量。所以微元体既有体属性又有点属性。体属性,比如微元体有大小,在弹性力学中推导平衡方程的时候就利用了这个属性;点属性,微元体只有一个位置信息,所以我们可以描述某点的应力。
可以这么理解:微元体无穷小,无穷小体首先是体,其次因为是无穷小,所以可以当成点。理解的秘诀在于无穷小!要有微积分的视角!
微元体的诡异之处正是它的巧妙之处。遥想笔者读大学的时候就感到这个模型的诡异。但一直没有深入思考并且转化为文字。直到笔者知晓了贝克莱,知晓了“贝克莱悖论”。
17世纪的一件大事就是微积分的问世,它一问世,就显示出它锐利无比的非凡威力,许多疑难问题都变得易如反掌。
但是,微积分理论的创立是不严谨的,对作为基本概念的无穷小量的理解与运用也是混乱的。因而,微积分从诞生时起就遭到了一些人的反对,贝克莱就是那个扛大旗的。贝克莱说,这是“依靠双重错误得到了不科学但却正确的结果”,因为无穷小量在最初的微积分理论中,一会儿说是0,一会儿又说不是0。因此,贝克莱嘲笑那无穷小量是“已死量的幽灵”。
这种攻击真正抓住了原始微积分理论中的缺陷,是切中要害的,数学史上称之为“贝克莱悖论”。
针对贝克莱的攻击,发现微积分的数学家曾试图通过完善自己的理论来解决,但都没有获得完全成功。这使他们陷入了异常尴尬的境地:一方面微积分在实际运用中大获全胜,另一方面其自身存在着逻辑矛盾。
了解这段历史后,你就知道了,觉得微元体很诡异,你并不孤独,因为大哲学家贝克莱也同样觉得无穷小量很诡异。但那是在18世纪!
学过物理都知道,光具有波粒二象性。按照这个描述方法,微元体则具有体点二象性。
当研究微元体本身时,微元体则具有体属性。比如平衡方程,几何方程。当研究结构时,微元体在相比之下就变成了点,所以我们可以描述某点的应力,某点的应变。




