Vienna整流器(二)--最近三矢量NTV调制

三电平空间矢量包含：最近三矢量NTV法和基于两电平等效的SVM法。相比于载波调制和DPWM调制，具有以下几点优势：

➤电压利用率较高，相比于传统的SPWM提高约15%，直流母线电压的输出范围更加宽了；

➤可以灵活地配置冗余小矢量来调整正负母线电压的平衡以及减小开关动作的次数，相比于传统的SPWM可以减少1/3；

➤矢量调制下的中点电流波动更小，在母线电容相同的情况下中点电压波动小，从而导致其输入电流谐波含量更小；

➤拥有更小的电感电流纹波，可以减小输入滤波电感的感量。

三电平空间矢量最早是应用于NPC型的变换器，后来拓展到了Vienna整流器中。下面我们来分别介绍一下子~

根据六个长矢量将空间分为六个扇区，即从0°到60°为第I扇区，逆时针依次增加60°为下一个扇区。由于整流二极管的单向导电性，每个扇区根据相电流的流向有的矢量为冗余矢量，故每个扇区应继续划分。根据传统三电平整流器进行SVPWM调制的原则，一般通过三条边界条件来进行扇区的判断，继而在扇区内进行小扇区的确定来进行矢量调制。

当给定任意参考矢量，将其坐标变换到两相静止坐标系下Uα和Uβ的值，且由三角变化可求出其在相邻两个矢量上的投影值D1和D2。不妨令X=2√3*Uβ/3，Y=Uα+√3*Uβ/3，Z=-Uα         +√3*Uβ/3，由这三个变量可表示各主扇区内参考矢量在相邻两矢量的投影，如下表所示：

下面我们以第I扇区为例，当参考矢量位于第I扇区时，为了利用其相邻的三个矢量来合成，需要将扇区进一步划分来计算各矢量作用时间，扇区的进一步划分见下图，划分为四个等边三角形区域：

             1号子扇区                                    2号子扇区

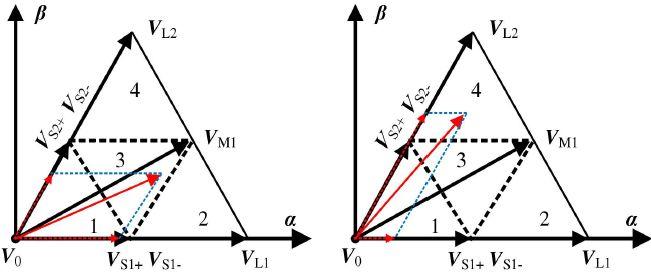
               3号子扇区                                   4号子扇区

我们为了方便各子扇区判断，需要对参考矢量在VL1、VL2上的投影进行归一化处理，令d1=D1/(UPN/3)和d1=D1/(UPN/3)，

可以通过下面的式子来进行判断：

由此我们可以得到扇区I的矢量合成分配表，如下所示：

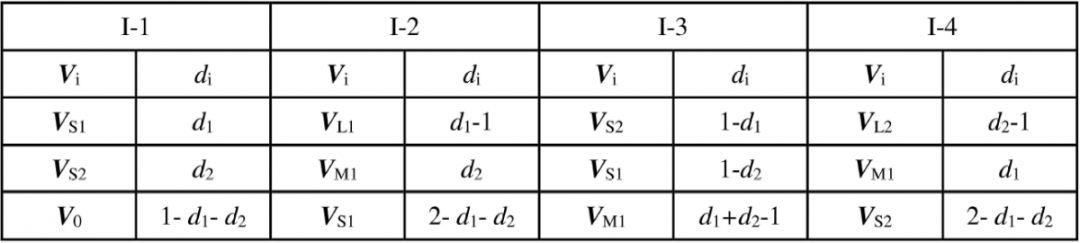
其中在扇区I-1和I-3中需要结合电流的流向来判断可以使用的小矢量，当参考矢量的相角满足φref＜30°时，B相电流满足ib＜0时，Vs1可取Vs1+(poo)和Vs1-(onn)，Vs2仅能取Vs2-(oon)；当参考矢量的相角满足30°＜φref＜60°时，B相电流满足ib＞0时，Vs1仅能取Vs1+(poo)，Vs2可取Vs2+(ppo)和Vs2-(oon)。另外在扇区I-1需要零矢量V0(ooo)来作为冗余矢量进行矢量补偿。

以扇区I-1为例来进行矢量序列的配置，要求每一次仅有一个开关管动作，这样不仅可以降低开关损耗，同时降低了开关动作产生的电磁干扰；另外采取对称的三角波进行调制产生来对称的PWM脉冲，通常采用七段式来进行矢量调制，其他扇区的矢量合成和作用时间以此类推。

据之前的分析可知，当参考矢量位于扇区I-1且ib＜0时，可以用来合成的基本矢量的状态有poo、onn、oon和ooo，其中状态o表示开关闭合，状态p和n均表示开关断开，且根据电流的流向自动切换，若要满足每次矢量切换仅有一个开关动作的话，那么可以排列的顺序有两种：poo、ooo、oon和onn、oon、ooo、poo。

那么，当参考矢量位于扇区I-1且ib＞0时，则有：oon、ooo、poo、ppo和ppo、poo、ooo、onn。z对应的脉冲波形和占空比如下图：

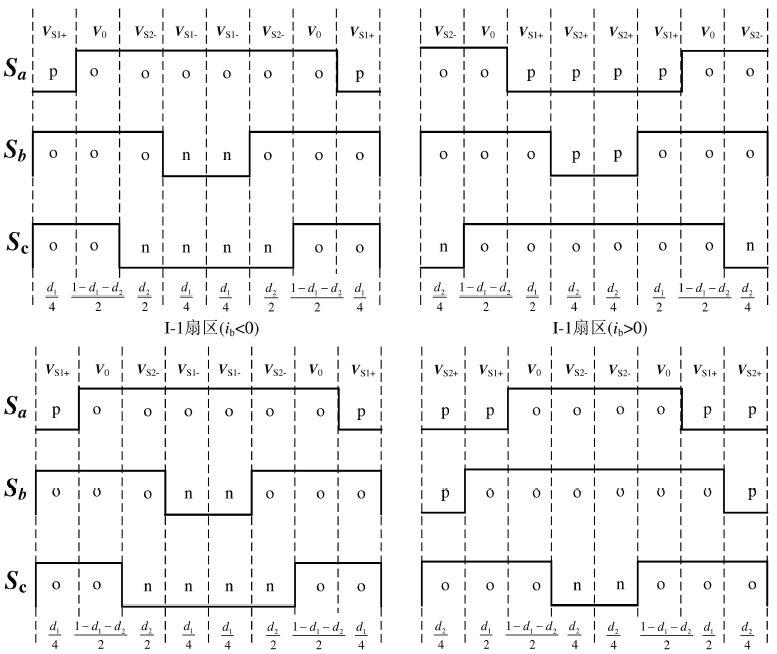
当ib＜0到ib＞0进行切换的时候，采用第一种组合需要标变换A相和C相的比较逻辑，而采用第二种组合时，则仅需变换B相开关的比较逻辑即可。所以，如果采用数字控制时，采用第二种组合可以简化程序。

综合上面说的，最近矢量NTV法的扇区划分从0°开始，每个扇区划分为4个子扇区，共有24个扇区。每个小扇区内矢量选择即其矢量作用时间均不相同，计算方式也有所差别。鉴于Vienna整流器的特殊性，同一扇区内可以使用的矢量还会受到输入电流的限制，且在电流过零点前后矢量序列的选取对开关逻辑的影响也需要纳入考虑范畴，所以这个过程的复杂性不言而喻了，如果大家遇到的话，感兴趣的可以花点工夫理解下。

定睛一看，写着写着都已经零点过半小时了，那关于另一种调制方式，我们明天再聊吧~

说明：本文来源功率半导体那些事儿；文中观点仅供分享交流，不代表本公 众 号立场，转载请注明出处，如涉及版权等问题，请您告知，我们将及时处理。