第二部分 PLL输出相位与Park变换矩阵输入角度之间的关系
“在使用4种派克(Park)变换矩阵时,怎样做到锁相环(PLL)输出相角与Park矩阵中的θ匹配?将PLL输出角度作为Park矩阵的θ角度时,为什么需要偏移90度?”

01.背景
图1至图4描述了abc三相静止坐标系与dq同步旋转坐标系之间的关系,在第一部分(点击可打开原文章)已经分别介绍过其对应Park变换矩阵,且图1和图2中θ为vd与va的夹角,而图3和图4中θ为vd与vβ负半轴的夹角。
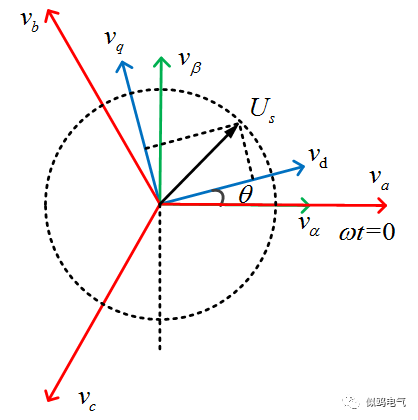
图1 abc三相静止坐标系与dq同步旋转坐标系的关系(1)

图2 abc三相静止坐标系与dq同步旋转坐标系的关系(2)
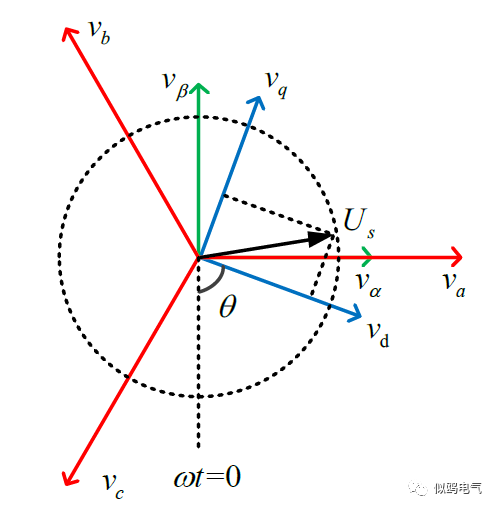
图3 abc三相静止坐标系与dq同步旋转坐标系的关系(3)

图4 abc三相静止坐标系与dq同步旋转坐标系的关系(4)
02.如何判断三相电压为“正弦形式”或“余弦形式”?
图5为物理中描述物体简谐运动的旋转矢量法示意图。当旋转矢量的初始位置为图中紫色点时,矢量旋转一周其值将经历A、0、-A、0的大小变化;当旋转矢量的初始位置为图中蓝色点时,矢量旋转一周其值将经历0、A、0、-A的大小变化。此处称以紫色点为初始位置的运动为余弦形式,而以蓝色点为初始位置的运动为正弦形式。对于图1至图4中的a相电压,由于a相电压参考轴与α轴正方向重合,所以图1至图4中的a相电压均为余弦形式,但由于图1、图2与图3、图4中θ的初始位置不同,导致PLL输出角的设置也有所不同。

图5 旋转矢量法示意图
图6为系统侧a相电压与PLL输出相位的关系,从图中可以看出PLL输出相角在0~2π之间变化,而且当a相电压为周期中第一个0值点(下一时刻将由0向正值增加),PLL输出相位也为0,由于PLL输出的是a相电压的相位,所以只有正弦形式的a相电压才能表现出如图6中的特征。

图6 系统侧a相电压与PLL输出相位的关系
综上所述,图1至图4中a相电压均为余弦形式,Park矩阵也是在余弦形式电压下推导所得,而PLL输出相位为正弦形式a电压的相位,所以PLL输出相位需要经过偏移才能输入给Park矩阵。
03.如何设置PLL,使其适用于第一、二种Park变换矩阵?
Park矩阵中一般取θ为a相电气量的相位,则可使d轴分量等于三相合成矢量的有效值,q轴分量等于0。
如前所述,在系统侧三相电压为余弦形式时推导得到第一种Park变换矩阵,而锁相环(PLL)的相位偏移设置为0时,其输出相位为系统侧三相电压为正弦形式时a相的相位,所以为了PLL输出相位与第一种Park矩阵匹配,需要将PLL输出的相位移相90度。
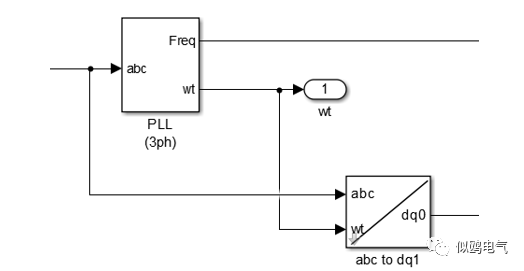
在Matlab/simulink中,可以将PLL输出相位减π/2,然后对2π取模得到Park所需的输入角度θ。

在PSCAD中:①可以直接在PLL模块中输入要偏移的角度(π/2);②也可以将偏移角度设置为0,然后像Matlab中那样将PLL输出相位减π/2,然后对2π取模值得到Park所需的输入角度θ,PSCAD中好像没有取模计算的模块,需要编写自定义模块。
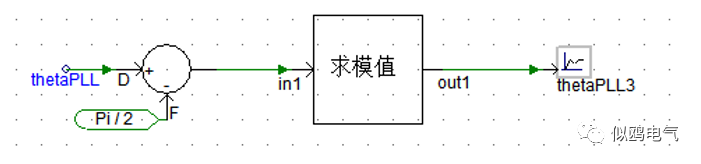
图7表示PLL输出角度偏移90度后与a相电压的关系,可见图中蓝线表示了余弦形式电压的相位变化情况。

图7 移相后a相电压与PLL输出相位的关系
04.如何设置PLL,使其适用于第三、四种Park变换矩阵?
虽然第三、四种Park变换矩阵也是在余弦形式电压下推导而得,但是Park矩阵中θ的参考轴却是vβ负半轴,θ的大小已经比a相电压小π/2,所以无需再将PLL输出角度偏移π/2。
05.总结
对于"第一部分 4种派克(Park)变换矩阵的由来(点击可打开原文章)"中的4种Park变换矩阵:第一种和第二种Park变换矩阵中的θ,需要将PLL输出角度偏移π/2才能与之匹配;第三种和第四种Park变换矩阵中的θ不需要对PLL输出角度偏移即可匹配。
以上纯属胡思乱堆,如有雷同,实属社会之幸,不喜轻喷。
后续发布预告
第三部分:在4种派克(Park)变换矩阵下,电流内环控制器表现出如下多种形式的原因(只考虑正常运行情况)。
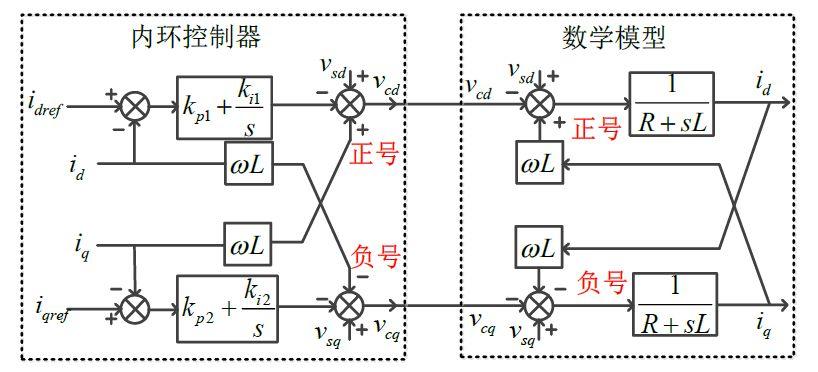
第1种电流内环
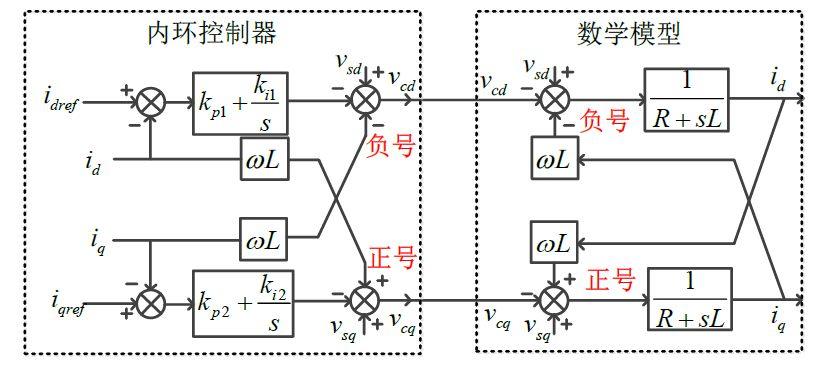
第2种电流内环
第四部分:在dq同步旋转坐标系下,系统侧瞬时有功功率和无功功率表现出如下多种形式的原因(P、Q除了直流分量外,还有基频分量和二倍频分量,此处未给出)。

说明:本文来源网络;文中观点仅供分享交流,不代表本公 众 号立场,转载请注明出处,如涉及版权等问题,请您告知,我们将及时处理。
- END -