DSP的FFT算法

#ifndef ZX_FFT_H_
#define ZX_FFT_H_
typedef float          FFT_TYPE;
#ifndef PI
#define PI             (3.14159265f)
#endif
typedef struct complex_st {
FFT_TYPE real;
FFT_TYPE img;
} complex;
int fft(complex *x, int N);
int ifft(complex *x, int N);
void zx_fft(void);
#endif /* ZX_FFT_H_ */

  
/*
 * zx_fft.c
 *
 * Implementation of Fast Fourier Transform(FFT)
 * and reversal Fast Fourier Transform(IFFT)
 *
 *  Created on: 2013-8-5
 *      Author: monkeyzx
 */
#include "zx_fft.h"
#include <math.h>
#include <stdlib.h>
/*
 * Bit Reverse
 * === Input ===
 * x : complex numbers
 * n : nodes of FFT. @N should be power of 2, that is 2^(*)
 * l : count by bit of binary format, @l=CEIL{log2(n)}
 * === Output ===
 * r : results after reversed.
 * Note: I use a local variable @temp that result @r can be set
 * to @x and won't overlap.
 */
static void BitReverse(complex *x, complex *r, int n, int l)
{
int i = 0;
int j = 0;
short stk = 0;
static complex *temp = 0;
temp = (complex *)malloc(sizeof(complex) * n);
if (!temp) {
return;
}
for(i=0; i<n; i++) {
stk = 0;
j = 0;
do {
stk |= (i>>(j++)) & 0x01;
if(j<l)
{
stk <<= 1;
}
}while(j<l);
if(stk < n) {             /* 满足倒位序输出 */
temp[stk] = x[i];
}
}
/* copy @temp to @r */
for (i=0; i<n; i++) {
r[i] = temp[i];
}
free(temp);
}
/*
 * FFT Algorithm
 * === Inputs ===
 * x : complex numbers
 * N : nodes of FFT. @N should be power of 2, that is 2^(*)
 * === Output ===
 * the @x contains the result of FFT algorithm, so the original data
 * in @x is destroyed, please store them before using FFT.
 */
int fft(complex *x, int N)
{
int i,j,l,ip;
static int M = 0;
static int le,le2;
static FFT_TYPE sR,sI,tR,tI,uR,uI;
M = (int)(log(N) / log(2));
/*
 * bit reversal sorting
 */
BitReverse(x,x,N,M);
/*
 * For Loops
 */
for (l=1; l<=M; l++) {   /* loop for ceil{log2(N)} */
le = (int)pow(2,l);
le2 = (int)(le / 2);
uR = 1;
uI = 0;
sR = cos(PI / le2);
sI = -sin(PI / le2);
for (j=1; j<=le2; j++) {   /* loop for each sub DFT */
//jm1 = j - 1;
for (i=j-1; i<=N-1; i+=le) {  /* loop for each butterfly */
ip = i + le2;
tR = x[ip].real * uR - x[ip].img * uI;
tI = x[ip].real * uI + x[ip].img * uR;
x[ip].real = x[i].real - tR;
x[ip].img = x[i].img - tI;
x[i].real += tR;
x[i].img += tI;
}  /* Next i */
tR = uR;
uR = tR * sR - uI * sI;
uI = tR * sI + uI *sR;
} /* Next j */
} /* Next l */
return 0;
}
/*
 * Inverse FFT Algorithm
 * === Inputs ===
 * x : complex numbers
 * N : nodes of FFT. @N should be power of 2, that is 2^(*)
 * === Output ===
 * the @x contains the result of FFT algorithm, so the original data
 * in @x is destroyed, please store them before using FFT.
 */
int ifft(complex *x, int N)
{
int k = 0;
for (k=0; k<=N-1; k++) {
x[k].img = -x[k].img;
}
fft(x, N);    /* using FFT */
for (k=0; k<=N-1; k++) {
x[k].real = x[k].real / N;
x[k].img = -x[k].img / N;
}
return 0;
}
/*
 * Code below is an example of using FFT and IFFT.
 */
#define  SAMPLE_NODES              (128)
complex x[SAMPLE_NODES];
int INPUT[SAMPLE_NODES];
int OUTPUT[SAMPLE_NODES];
static void MakeInput()
{
int i;
for ( i=0;i<SAMPLE_NODES;i++ )
{
x[i].real = sin(PI*2*i/SAMPLE_NODES);
x[i].img = 0.0f;
INPUT[i]=sin(PI*2*i/SAMPLE_NODES)*1024;
}
}
static void MakeOutput()
{
int i;
for ( i=0;i<SAMPLE_NODES;i++ )
{
OUTPUT[i] = sqrt(x[i].real*x[i].real + x[i].img*x[i].img)*1024;
}
}
void zx_fft(void)
{
MakeInput();
fft(x,128);
MakeOutput();
ifft(x,128);
MakeOutput();
}

程序在TMS320C6713上实验，主函数中调用zx_fft()函数即可。

FFT的采样点数为128，输入信号的实数域为正弦信号，虚数域为0，数据精度定义FFT_TYPE为float类型，MakeInput和MakeOutput函数分别用于产生输入数据INPUT和输出数据OUTPUT的函数，便于使用CCS 的Graph功能绘制波形图。这里调试时使用CCS v5中的Tools -> Graph功能得到下面的波形图（怎么用自己琢磨，不会的使用CCS 的Help）。

输入波形

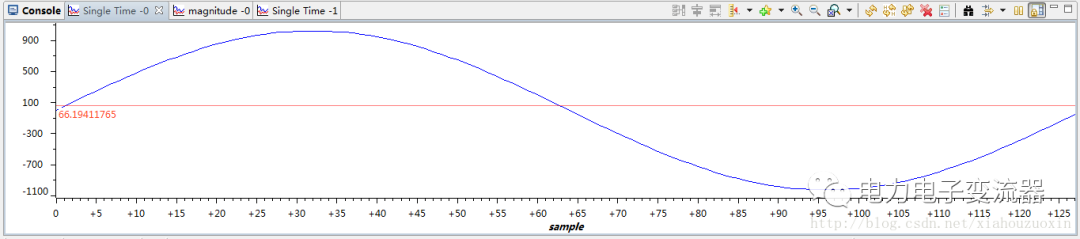
输入信号的频域幅值表示

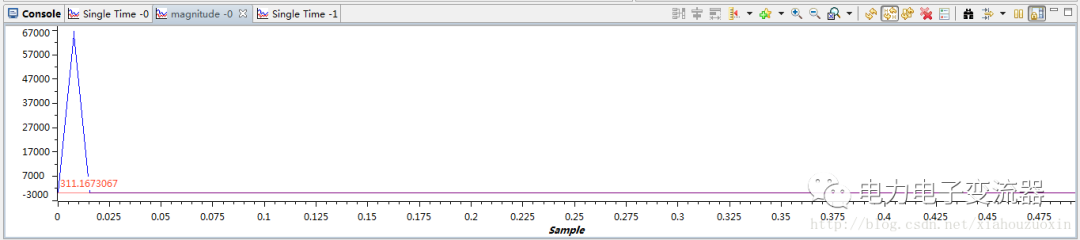
FFT运算结果

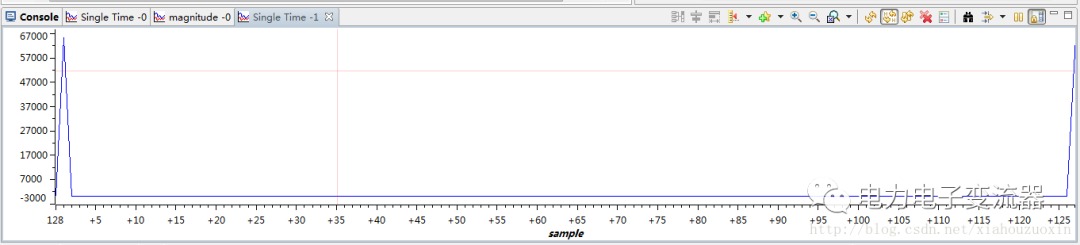
对FFT运算结果逆变换(IFFT)

如何检验运算结果是否正确呢？有几种方法：

（1）使用matlab验证，下面为相同情况的matlab图形验证代码

  
SAMPLE_NODES = 128;
i = 1:SAMPLE_NODES;
x = sin(pi*2*i / SAMPLE_NODES);
subplot(2,2,1); plot(x);title('Inputs');
axis([0 128 -1 1]);
y = fft(x, SAMPLE_NODES);
subplot(2,2,2); plot(abs(y));title('FFT');
axis([0 128 0 80]);
z = ifft(y, SAMPLE_NODES);
subplot(2,2,3); plot(abs(z));title('IFFT');
axis([0 128 0 1]);