弹簧振子看模态分析
本文摘要(由AI生成):
模态是结构系统的固有振动特性,可解耦为N个正交的单自由度振动系统,每个模态有特定参数。模态分析通过计算或试验得出模态参数,了解结构在易受影响的频率范围内的振动特性及响应结果。弹簧振子的模态分析显示,固有频率小的先振动,整体模态分析可拆解为单自由度部分,产生相应模态阶数。
模态是结构系统的固有振动特性。线性系统的自由振动被解耦合为N个正交的单自由度振动系统,对应系统的N个模态。每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。通过结构模态分析法,可得出机械结构在某一易受影响的频率范围内各阶模态的振动特性,以及机械结构在此频段内及在内部或外部各种振源激励作用下的振动响应结果,再由模态分析法获得模态参数并结合相关试验,借助这些特有参数用于结构的重新设计。
通过这个弹簧振子的模态分析,我们可以知道,模态分析当中,对于分析者不需要施加载荷只需要把产品的实际约束定义好,接下来看在这些约束下,产品本身的固有频率是多少就可以。模型如下:

边界条件,以及施加不同弹簧刚度条件下,各个弹簧振子的固有频率不一样,那么最后的分析表明,只要固有频率小的先振动,也就表明对于整体模态分析其实就是拆解成单自由度的部分,能先达到固有频率的就是振动频率,有多少自由度,就会产生多少模态阶数。
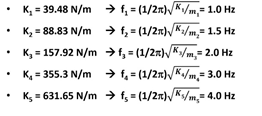

登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2020-05-29
最近编辑:3月前
相关推荐
最新文章
热门文章




