07 两曲面的接触仿真分析

专注于仿真分析和振动分析

00 导读

    在笔者前作《05 球体和弹性半空间的接触分析》中，分析了一个曲面和平面的接触，仿真结果和Hertz理论解析结果高度一致。验证了数值仿真的可靠性。本文研究两个曲面之间的接触，从Hertz理论角度来说，曲面和平面或者曲面接触本质是一样的，但仿真实践上，会呈现出更多的规律。

01 研究背景

Hertz接触理论的假设如下：

1）线弹性假设，材料线性；

2）小变形假设，几何线性：

3）无摩擦假设，接触非线性；

02 几何模型

几何模型如下图所示。假设球体是刚性的。因为和接触面积相比，长方体足够大，可以认为是弹性半空间，并且长方体上有内凹曲面。

03 材料模型

本文使用到的所有材料参数如下。

    线弹性。

04 网格划分

    网格的整体和局部如下图所示。

05 边界条件

约束长方体底部，刚性球垂直向下施加位移。

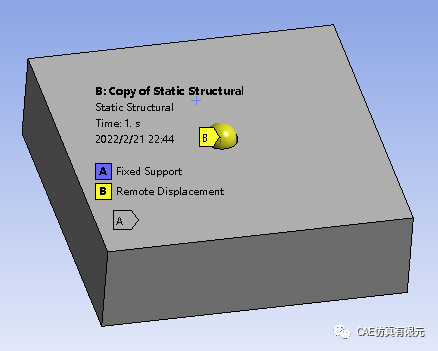
06 仿真分析

    假设刚性球的垂直位移是0.5mm，为球曲率半径的1/10。

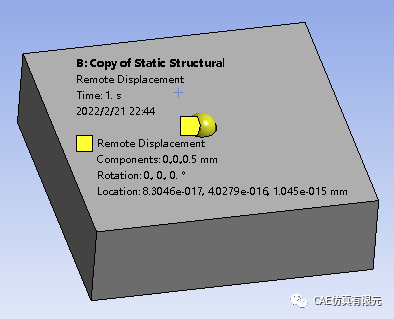
    垂向最大位移0.5mm。

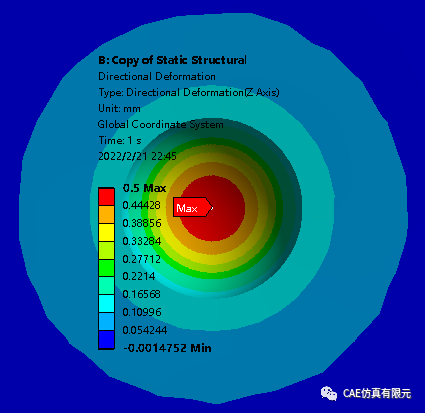
    接触穿透为0。

    最大接触压力如下图所示 。

    对比内凹曲面不同的曲率半径，如下表所示。

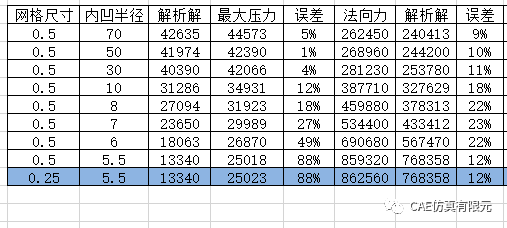
    内凹曲率半径和最大压力计算误差如下图所示。当内凹半径减小时，根据Hertz理论，接触区域会增大，最大接触压力会降低，仿真呈现了这个规律，但仿真解的误差增加了。

    固定内凹曲率半径为5.5mm，改变垂向最大位移，如下表所示。

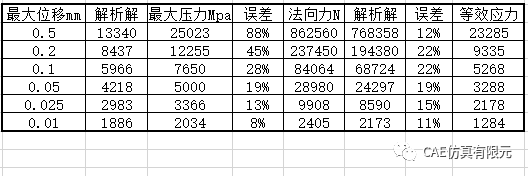
    最大垂向位移和最大压力计算误差如下图所示。当最大位移减少时，仿真解的误差也会减小。

    在Hertz理论中，两个曲面接触可以计算出等效曲率半径，如下图所示。

    综上可得两个结论。

    1）两个曲面之间的接触可以使用有限元仿真进行求解。

    2）对于一凹一凸的曲面接触，两个曲面半径越接近，则小位移下仿真解的精度才较高；