1.1声学波动方程
通过声波连续性方程、声波运动方程、理想气体状态方程，得到了著名的Helmholtz声学波动方程：
式中：拉普拉斯算子
； 
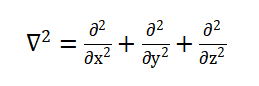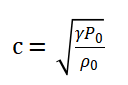为声波在流体介质中的传播速度；
c与时间t的关系为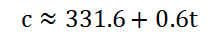
；
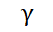为气体定压比热容与定容比热容之比，
；
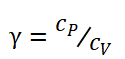P为流体中的总声压；
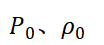分别为静态情况下的声压、密度；
q为微元体内单位体积的体积速度。
1.2声学边界条件
对于Helmholtz声学波动方程，只要确定边界条件，其解就是唯一的。稳态声场的边界条件一般分为三类：
(1) 已知结构表面的声压（Dirichlet边界）；
(2) 已知结构表面的法向振动速度（Neuman边界）；
(3) 已知结构表面的法向阻抗（Robin边界）。
对于特定声学问题，三种类型的边界条件可以同时存在于同一模型中；对于外部声学问题，声场在无穷远处还应该满足Sommerfeld辐射条件，即无限远处不存在反射声波。
本次机床主轴电机的结构振动声辐射案例，就是将电机结构计算后表面的振动速度，转换成电机表面的声压边界，并且映射到空气表面的声边界面上，完成电机运行时的振动声辐射问题的分析。
1.3声学边界元
对于上述的声学波动方程，可以用数值方法得到其满足边界条件的解。常用的数值方法有声学有限元法和声学边界元法。
声学有限元法是采用整个分析域的离散，但随着声学仿真模型的日益精细与庞大，网格划分费时费力；对于无限域声学问题，有限元方法还需要结合一些特殊的方法进行问题转换。相比声学有限元，声学边界元法有如下几方面明显的优势：
(1) 只需在结构边界上划分单元，建模简单、单元数目少；
(2) 只需在边界面上进行离散和计算，将三维问题转化为二维问题，达到了降维的效果；
(3) 边界积分方程直接采用解析形式的基本解，计算精度更高；
(4) 基本解自动满足无穷远处边界条件，适合处理无限域问题。
1.4声学积分方程
跟有限元法、有限差分法等基于微分方程方法不同，声学边界元是基于积分方程的数值计算方法。在声场中，求解不在结构边界单元上的任意一点处的声学结果，通常需要先得到满足一定条件的Helmholtz微分方程基本解，称为格林函数，再对满足格林函数的声学波动方程进行积分获得。
边界元法虽然较有限元而言，减少了网格、降低了问题维数，但计算时由于系数矩阵是满秩矩阵，计算存储量、计算效率上，并没有明显优势。
1.5快速算法
快速算法是解决传统边界元的存储、计算效率问题，最为有效、应用最广泛的一种快速边界元方法。
AcousticBEM提供的快速算法包括：快速直接法、快速多极子、快速自适应、快速高频算法，适用于计算不同规模、不同频率范围的声学问题；针对电机模型的规模大小，采用快速自适应法能保证计算精度的同时，实现最高效的求解效率。下面我们就基于PERA SIM AcousticBEM的快速自适应声学求解功能，完成机床主轴电机振动辐射声场分析。
