基于PERA SIM的机床主轴电机辐射声场分析

6月前浏览25870

安世亚太声学工程师

黄锦耀

前言

机床作为工业母机是装备制造业的核心和基础，高端数控机床更是制造业升级发展的引擎。我国高端制造行业需要高速、高精、多轴联动的高档数控机床，《中国制造2025》战略纲领中明确指出，至2025年中国机床数控化率将提升至60%以上。而高端产品的国产化率目前仍然低于10%，数控化率提升空间巨大。同时随着下游产业的不断升级发展，国产数控机床行业加速发展，尤其是高端数控机床需求旺盛，实现数控机床核心零部件技术的国产替代是行业亟待解决的瓶颈问题。随着数控机床产业的发展和人们环保理念的提高，机床运行过程中的噪声污染越来越受到重视，噪声是检验机床产品合格与否的重要指标之一。

目前，有限元、边界元方法在求解声学问题中被广泛应用。其中，声学边界元法只需在结构边界建模，可以极大减少分析对象，并且边界积分方程的基本解自动满足无穷远处的边界条件，非常适合处理电机振动声辐射问题。

PERA SIM AcousticBEM是安世亚太自主开发的一款声学边界元分析软件，基于PERA SIM通用仿真软件架构，可以实现与结构、电磁、声学等物理场的耦合分析计算。AcousticBEM声学边界元模块结合了快速多极子、自适应交叉逼近等算法，在计算精度得到保证的前提下，效率上也实现了若干数量级的提升。

本文借助声学边界元软件中的快速自适应交叉逼近算法完成了电机全空间振动声辐射分析，展现了软件丰富的操作功能，并且与国际成熟软件的声场计算结果对比，验证了快速算法的准确性，为学者和工程师提供了声学分析的一种新方法。

1. 快速多极子边界元法

1.1声学波动方程

通过声波连续性方程、声波运动方程、理想气体状态方程，得到了著名的Helmholtz声学波动方程：

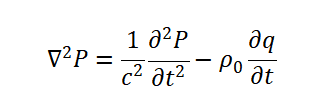
式中：拉普拉斯算子

；

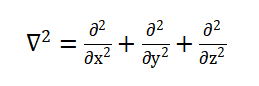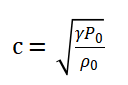为声波在流体介质中的传播速度；

c与时间t的关系为；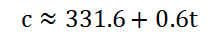

为气体定压比热容与定容比热容之比，；

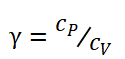P为流体中的总声压；

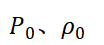分别为静态情况下的声压、密度；

q为微元体内单位体积的体积速度。

1.2声学边界条件

对于Helmholtz声学波动方程，只要确定边界条件，其解就是唯一的。稳态声场的边界条件一般分为三类：

(1) 已知结构表面的声压（Dirichlet边界）；

(2) 已知结构表面的法向振动速度（Neuman边界）；

(3) 已知结构表面的法向阻抗（Robin边界）。

对于特定声学问题，三种类型的边界条件可以同时存在于同一模型中；对于外部声学问题，声场在无穷远处还应该满足Sommerfeld辐射条件，即无限远处不存在反射声波。

本次机床主轴电机的结构振动声辐射案例，就是将电机结构计算后表面的振动速度，转换成电机表面的声压边界，并且映射到空气表面的声边界面上，完成电机运行时的振动声辐射问题的分析。

1.3声学边界元

对于上述的声学波动方程，可以用数值方法得到其满足边界条件的解。常用的数值方法有声学有限元法和声学边界元法。

声学有限元法是采用整个分析域的离散，但随着声学仿真模型的日益精细与庞大，网格划分费时费力；对于无限域声学问题，有限元方法还需要结合一些特殊的方法进行问题转换。相比声学有限元，声学边界元法有如下几方面明显的优势：

(1) 只需在结构边界上划分单元，建模简单、单元数目少；

(2) 只需在边界面上进行离散和计算，将三维问题转化为二维问题，达到了降维的效果；

(3) 边界积分方程直接采用解析形式的基本解，计算精度更高；

(4) 基本解自动满足无穷远处边界条件，适合处理无限域问题。

1.4声学积分方程

跟有限元法、有限差分法等基于微分方程方法不同，声学边界元是基于积分方程的数值计算方法。在声场中，求解不在结构边界单元上的任意一点处的声学结果，通常需要先得到满足一定条件的Helmholtz微分方程基本解，称为格林函数，再对满足格林函数的声学波动方程进行积分获得。

边界元法虽然较有限元而言，减少了网格、降低了问题维数，但计算时由于系数矩阵是满秩矩阵，计算存储量、计算效率上，并没有明显优势。

1.5快速算法

快速算法是解决传统边界元的存储、计算效率问题，最为有效、应用最广泛的一种快速边界元方法。

AcousticBEM提供的快速算法包括：快速直接法、快速多极子、快速自适应、快速高频算法，适用于计算不同规模、不同频率范围的声学问题；针对电机模型的规模大小，采用快速自适应法能保证计算精度的同时，实现最高效的求解效率。下面我们就基于PERA SIM AcousticBEM的快速自适应声学求解功能，完成机床主轴电机振动辐射声场分析。

2. 边界元模型的建立

2.1 PERA SIM声学边界元模块

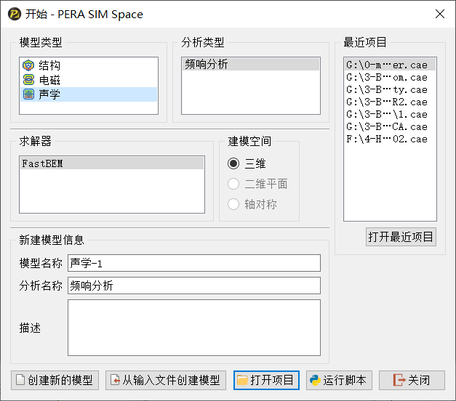
打开PERA SIM Space工作台，进入软件启动界面，模型类型支持结构、电磁、声学等三大物理场，选择声学频响分析，进入声学物理场分析场景，目前支持3维声学边界元计算：

2.2 主轴电机模型

PERA SIM前处理器，提供了丰富的数据接口，支持IGES、STEP等几何模型数据的导入；以及ANSYS（cdb、inp、dat）、ABAQUS（inp）、NASTRAN（bdf）等软件网格模型数据的导入；同时，可以完成简单的草图绘制、几何模型处理、添加声场面几何等功能。

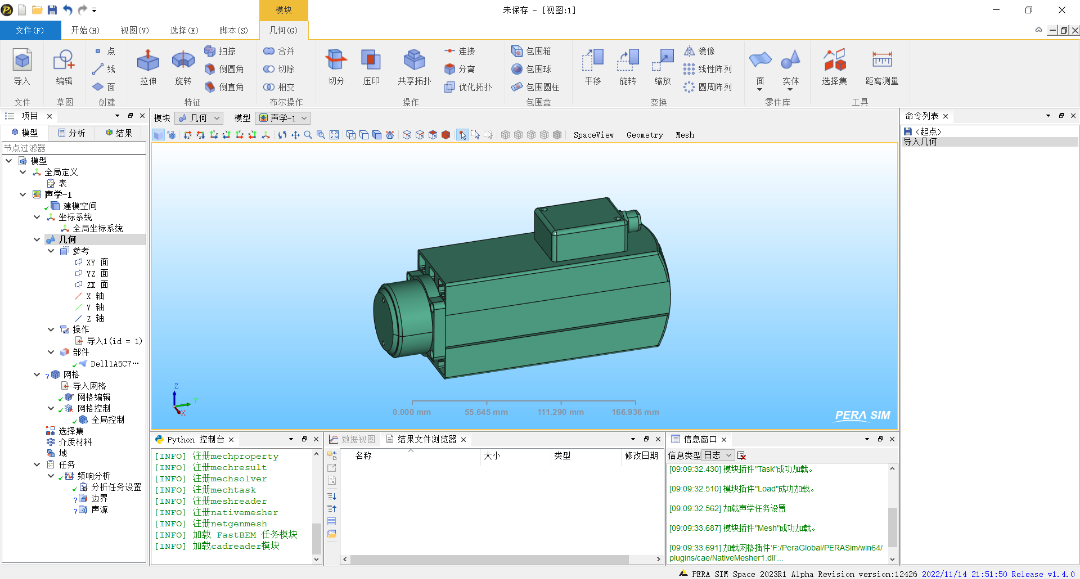
本文利用声学边界元模块，求解主轴电机固定于机床内部，接触工件受力后电机振动，形成辐射声场的问题，需要考虑电机结构与声场的耦合，导入电机模型如下图所示：

2.3 网格模块

PERA SIM提供了丰富的网格划分算法，支持对1D、2D、3D模型的网格划分，可以通过全局网格控制、局部网格控制等功能实现几何模型的高质量划分。在声学分析中，为满足计算精度，要求划分的最大单元边长要小于计算频率最短波长的1/6，即最大单元的边长L要满足：

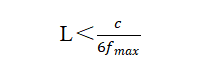
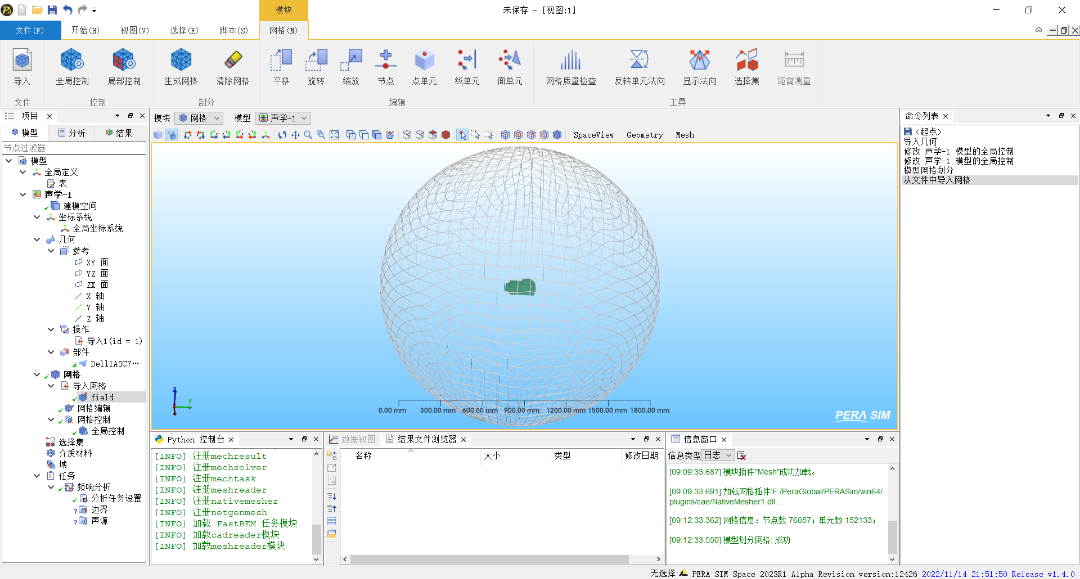
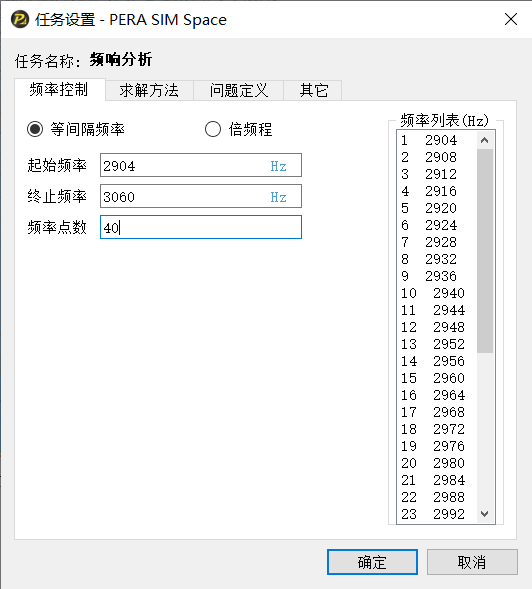
本案例依据电机工作时的最高频率：3060Hz。基于上述网格划分尺寸的要求，采用全局网格控制功能，离散模型共产生152133个单元，76057个节点；并且提供网格质量检查功能，单元法向检查和反转功能，实现内场声学或外场声学问题的控制选择；另外，还需要导入外部的球形声场面网格。

分析网格模型如下图所示：

2.4分析设置

进入“属性”模块，首先，需要确定声学环境中的声介质类型：整个分析区域是空气，密度设为1.2kg/m3、声速设为343m/s；设置参考参数对声学计算的结果——声压、声强度进行声级处理。

其次，确定声学分析中的网格类型，本案例中电机壳体表面的网格类型为电机声学分析网格，外部球面类型为声场面；属性设置如下图所示：

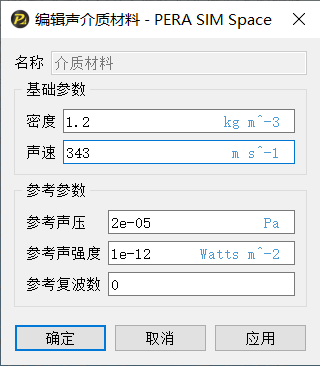
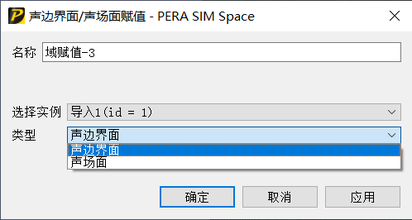
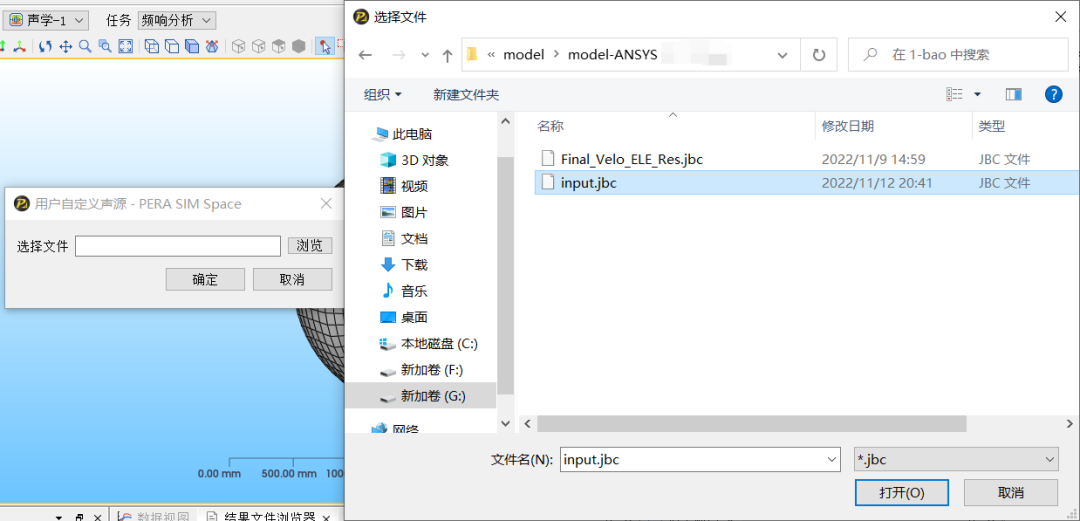
进入“边界”模块，完成声边界条件的设置。机床电机振动辐射噪声分析是由结构振动产生声音，需要考虑声场与振动的耦合。主轴电机工作时接触工件受到了反作用力，引起了电机振动，该振动过程可以在PERA SIM Mechanical中完成，获得电机壳体表面的压力，该压力通过映射处理，按用户自定义的方式作为电机声压边界，在AcousticBEM中完成振动声辐射分析；边界设置如下图所示：

进入“任务”模块，完成分析频率范围、求解方法、空间范围的设置。

本案例分析频率与结构分析的频率范围一致，选择2904Hz到3060Hz按4Hz等间隔递增；主轴电机振动声辐射这种小规模求解计算问题，空间范围在问题定义中设置为全空间，求解方法选择快速自适应交叉方法；声学边界面及场面的高斯积分点选择9，提高声学积分结果的精度。求解设置如下图所示：

3.计算结果分析

PERA SIM后处理可以查看电机表面及球形外声场的声压实部值和虚部值、以及声压Magnitude、声压级SPL（dB）等结果。下图为不同频率下PERA SIM快速自适应算法求得的电机表面及辐射声场的声压分布dB云图，以及与Virtual Lab结果对比展示：

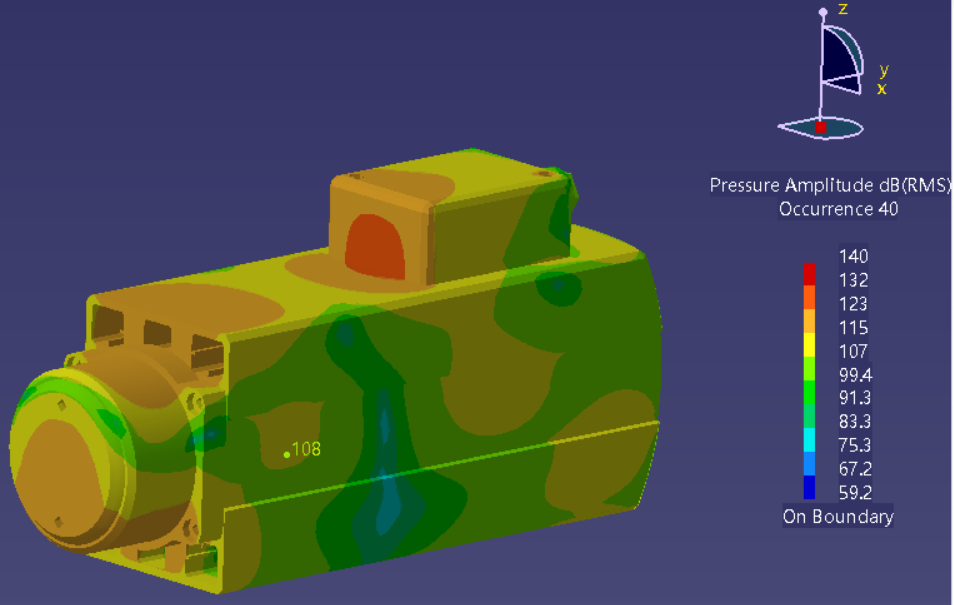
电机表面声压级云图对比
PERA SIM-2904Hz	Virtual Lab-2904Hz

PERA SIM -3060Hz	Virtual Lab-3060Hz

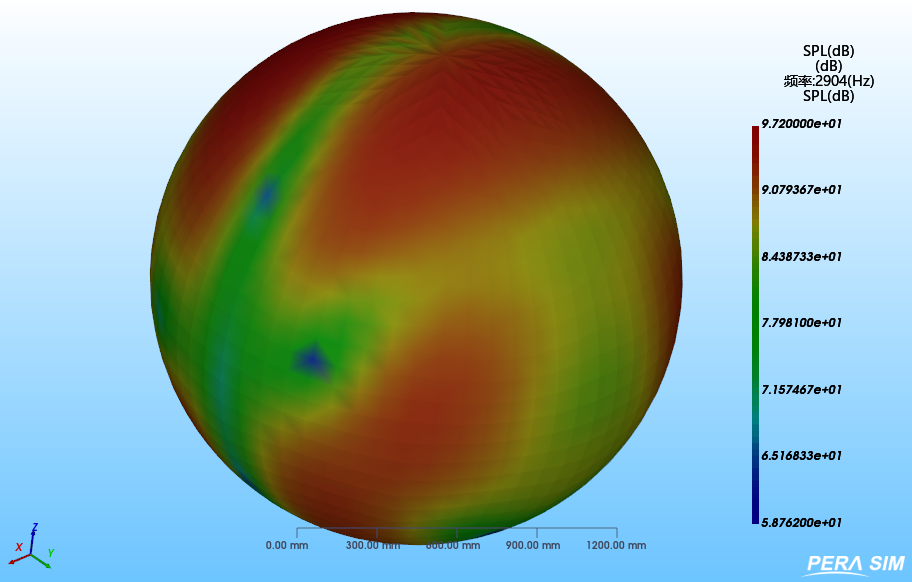
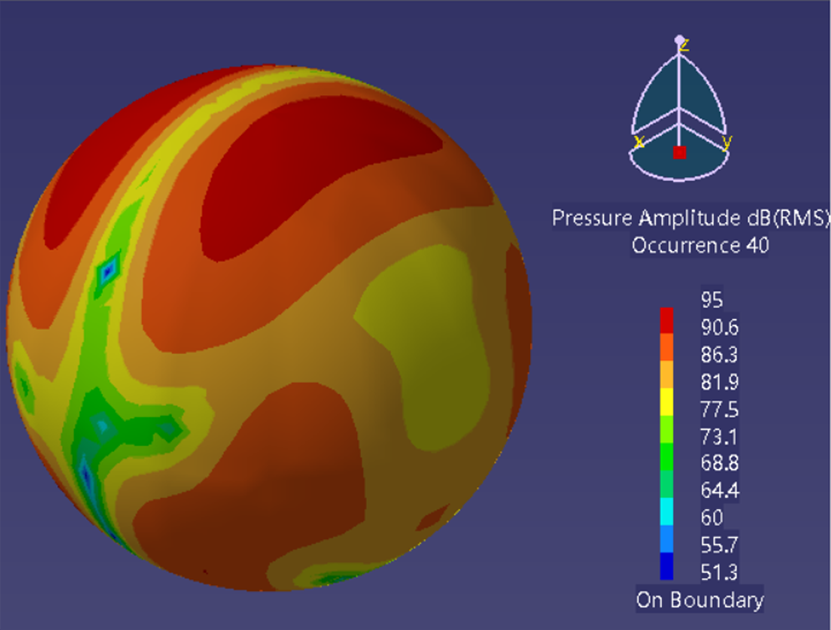
声场面声压级云图对比
PERA SIM -2904Hz	Virtual Lab-2904Hz

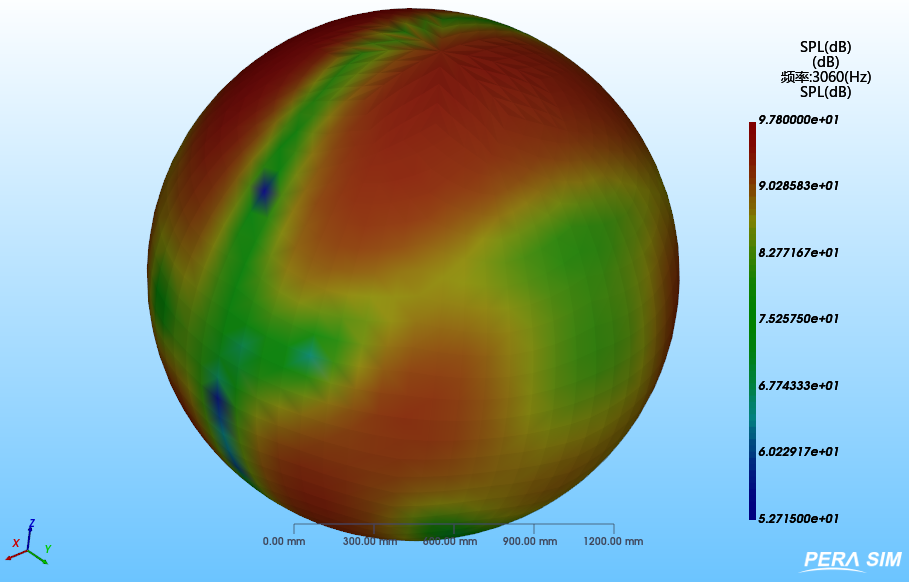
PERA SIM -3060Hz	Virtual Lab-3060Hz

PERA SIM求解器可以获得球形声场面、远场的声学结果，并在后处理中通过图表形式显示。电机声场面上不同频率的最大声压值，以及不同频率下远场的声功率大小，声学曲线结果如下：

PERA SIM、Virtual Lab结果对比

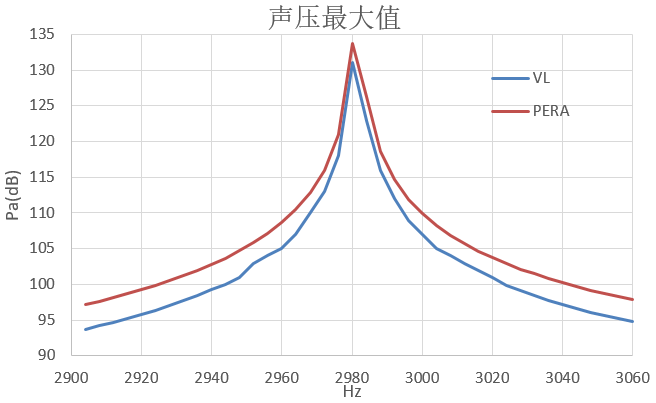
球形声场面

最大声压级

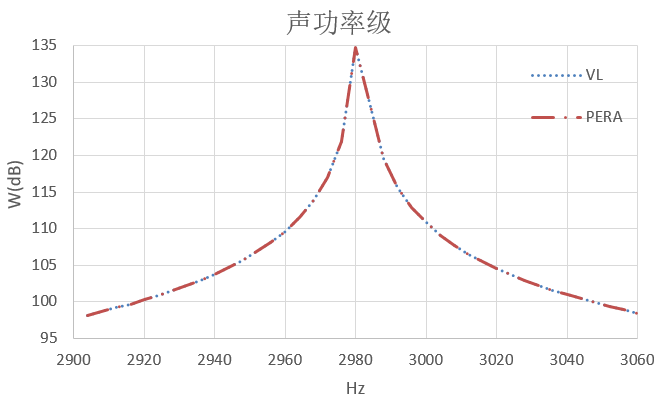
远场

声功率级

4.结论

本文基于安世亚太自主声学边界元软件PERA SIM AcousticBEM，计算机床主轴电机的振动辐射噪声，实现了网格划分、声学边界条件设置、快速求解到结果后处理的完整分析流程。同时，在相同的边界和求解参数的条件下，与国外商用软件LMS Virtual Lab计算结果对比，发现PERA SIM的声压分布、声功率级大小基本保持一致，声场面上的最大声压级结果较Virtual Lab高3dB左右，误差在3%以内，能保证较高的计算精度。