fluent中RNG k-ε湍流模型介绍
本文摘要(由AI生成):
RNG k-ε模型是一种基于重整化群理论的湍流模型,它改进了标准k-ε模型,提高了高速流动和旋涡流动的准确性。RNG模型提供了湍流普朗特数的解析公式,并考虑了低雷诺数的影响。RNG理论导出了湍流粘度的微分方程,允许模型更好地处理低雷诺数和近壁流。RNG模型还提供了涡流修正选项,以考虑平均流中旋转或涡流的影响。
RNG k-ε模型是使用一种称为重整化群理论的统计方法推导出来的。它是在形式上类似于standard k-ε模型,但包括以下改进:
RNG模型在其ε方程中增加了一项,提高了高速流动的准确性。
RNG模型考虑了涡流对湍流的影响,提高了旋涡流动的精度。
RNG理论提供了湍流普朗特数的解析公式,而standard k-ε使用用户指定的常数值。
虽然标准k-ε模型是高雷诺数模型,RNG微分公式理论提供了一种从分析中获得有效的粘度,考虑低雷诺数的影响,然而,这个特性的有效使用取决于对近壁区域的适当处理。
01—RNG k-ε Model的输运方程
RNG k-ε湍流模型来源于瞬态n - s方程,用一种称为重整化群(RNG)的数学方法。模型中的常数分析推导结果不同于standard k-ε模型,在k和ε输运方程中增加了项。RNG k-ε模型形式上类似于standard k-ε模型:
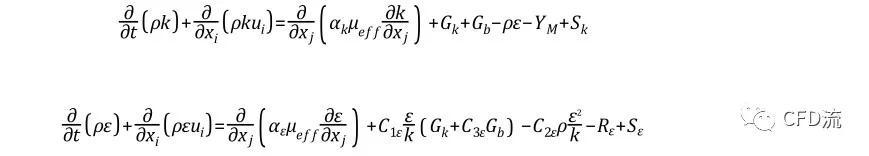
G_k表示平均速度梯度引起的湍流动能的产生;
G_b是由浮力产生的湍流动能;
Y_M表示可压缩湍流中波动膨胀对总耗散率的贡献;
α_k和α_ε分别是k和ε有效普朗特数的倒数;
S_k和S_ε是用户定义的源项。
02—模型的有效粘度
RNG理论中的尺度消除过程导出了湍流粘度的微分方程:


将上述方程积分以获得有效湍流传输如何随有效雷诺数(或涡流标度)变化的准确描述,从而允许模型更好地处理低雷诺数和近壁流。
在高雷诺数极限下,

03—RNG漩涡修正
湍流一般受平均流中旋转或涡流的影响。ANSYS Fluent中的RNG模型提供了一个通过适当修改湍流粘度来考虑涡流或旋转影响的选项。修改后的函数形式如下:

04—求有效普朗特数的倒数
有效普朗特数的倒数α_k和α_ε的计算公式由RNG理论解析推导如下:
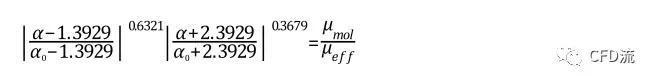
RNG k - ε和standard k -ε 模型之间的主要区别在于ε方程给出的附加项






