首页/文章/ 详情

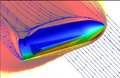
流体力学中的“数”-雷诺数

张老师

1年前浏览6504

1.雷诺数表达式

雷诺数（Reynolds number）一种可用来表征流体流动情况的无量纲数，它是流体惯性力与粘性力的量度比值，其定义式：

Re=ρvd/μ

其中：其中v、ρ、μ分别为流体的流速、密度与黏性系数，d为一特征长度。

2.雷诺数的作用

雷诺数是一个无量纲量，主要作用是判断流体的流动状态，层流还是湍流。

层流：液体分层流动，相临两层液体间只作相互滑动，流层间没有横向混杂。

湍流（紊流）：当流体流速超过某一数值时，流体不再保持分层流动，而可能向各个方向运动，有垂直于管轴方向的分速度，各流层将混淆起来，并有可能出现涡流，这种流动状态叫湍流。

雷诺数较小时，黏滞力对流场的影响大于惯性力，流场中流速的扰动会因黏滞力而衰减，流体流动稳定，为层流；反之，若雷诺数较大时，惯性力对流场的影响大于黏滞力，流体流动较不稳定，流速的微小变化容易发展、增强，形成紊乱、不规则的紊流流场。

临界雷诺数（critical Reynold’s number），当流体在管道中、板面上或具有一定形状的物体表面上流过时，流体的一部或全部会随条件的变化而由层流转变为湍流，此时，摩擦系数、阻力系数等会发生显著的变化。转变点处的雷诺数即为临界雷诺数。

在圆管流动中，区分层流和湍流两种流态的临界雷诺数Red=2000或2300；而在平板边界层内，区分层流边界层和湍流边界层的临界雷诺数Red=3.2×10^5。所以，Red=2000或2300并不是区分层流和湍流两种流态的唯一数值，该数值仅用于判断圆管流动的流动状态。

通过雷诺实验人们认识到，流动存在以下三种不同的状态。第一种，流体的质点之间互不掺混、质点的运动轨迹为有条不紊的层状流动，称为层流；第二种，流体的质点之间相互掺混、质点的运动轨迹为杂乱无章的流动，称为紊流；第三种，表现为层流到紊流或紊流到层流的过渡，称为过渡状态。随流速的变化而呈现不同的流动状态，是自然界中一切流体运动普遍存在的物理现象。